График параболы, с примерами построения

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция, и с чем ее едят. Если ты считаешь себя профи по части квадратичных функций, добро пожаловать. Но если нет, тебе стоит прочитать тему «Квадратичная функция».

Начнем с небольшой проверки:

1. Как выглядит квадратичная функция в общем виде (формула)?
2. Как называется график квадратичной функции?
3. Как влияет старший коэффициент на график квадратичной функции?

Если ты сходу смог ответить на эти вопросы, продолжай читать. Если хоть один вопрос вызвал затруднения, перейди по ссылке.

• Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
• Ну что же, вот она:  .
• Давай вкратце вспомним, что делают коэффициенты.

1. Старший коэффициент   отвечает за «крутизну» параболы, или, по-другому, за ее ширину: чем больше  , тем парабола у́же (круче), а чем   меньше, тем парабола шире (более пологая).
2. Свободный член   – это координата пересечения параболы с осью ординат.
3. А коэффициент   каким-то образом отвечает за смещение параболы от центра координат. Вот об этом сейчас подробнее.

С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?

Это вершина. А как найти координаты вершины, помнишь?

1. Абсцисса ищется по такой формуле:
2.  .
3. Вот так: чем больше  , тем левее смещается вершина параболы.
4. Ординату вершины можно найти, подставив   в функцию:
5.  .

Подставь сам и посчитай. Что получилось?

• Если сделать все правильно и максимально упростить полученное выражение, получится:
•  .
• Получается, что чем   больше по модулю, тем выше будет вершина параболы.

Перейдем, наконец, к построению графика. Самый простой способ – строить параболу, начиная с вершины.

1. Пример:
2. Построить график функции  .
3. Решение:
4. Для начала определим коэффициенты:  .
5. Теперь вычислим координаты вершины:
6. А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково. Значит, если мы построим параболу   и переместим ее вершиной в точку  , получится нужный нам график:

Просто, правда?

Остается только один вопрос: как быстро рисовать параболу? Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?

Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.

Рассмотрим простейшую параболу  . Построим ее по   точкам:

Закономерность здесь такая. Если из вершины сместиться вправо (вдоль оси  ) на  , и вверх (вдоль оси  ) на  , то попадем в точку параболы. Дальше: если из этой точки сместиться вправо на   и вверх на  , снова попадем в точку параболы.

Дальше: вправо на   и вверх на  . Дальше что? Вправо на   и вверх на  . И так далее: смещаемся на   вправо, и на следующее нечетное число вверх.

То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):

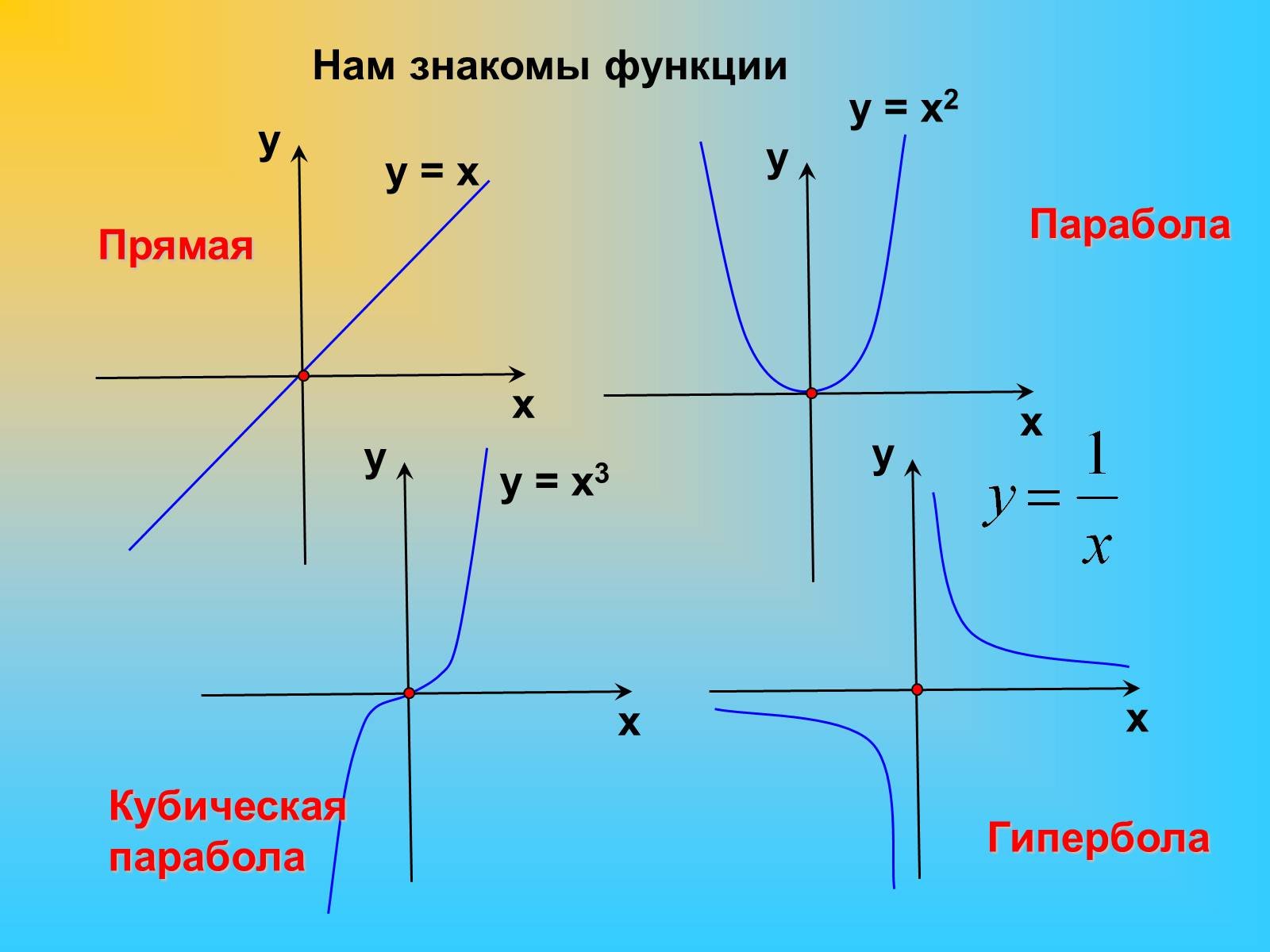
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным  . Например, нам стало известно, что вершина параболы находится в точке  . Построй (самостоятельно, на бумаге) эту параболу.

Построил?

Должно получиться так:

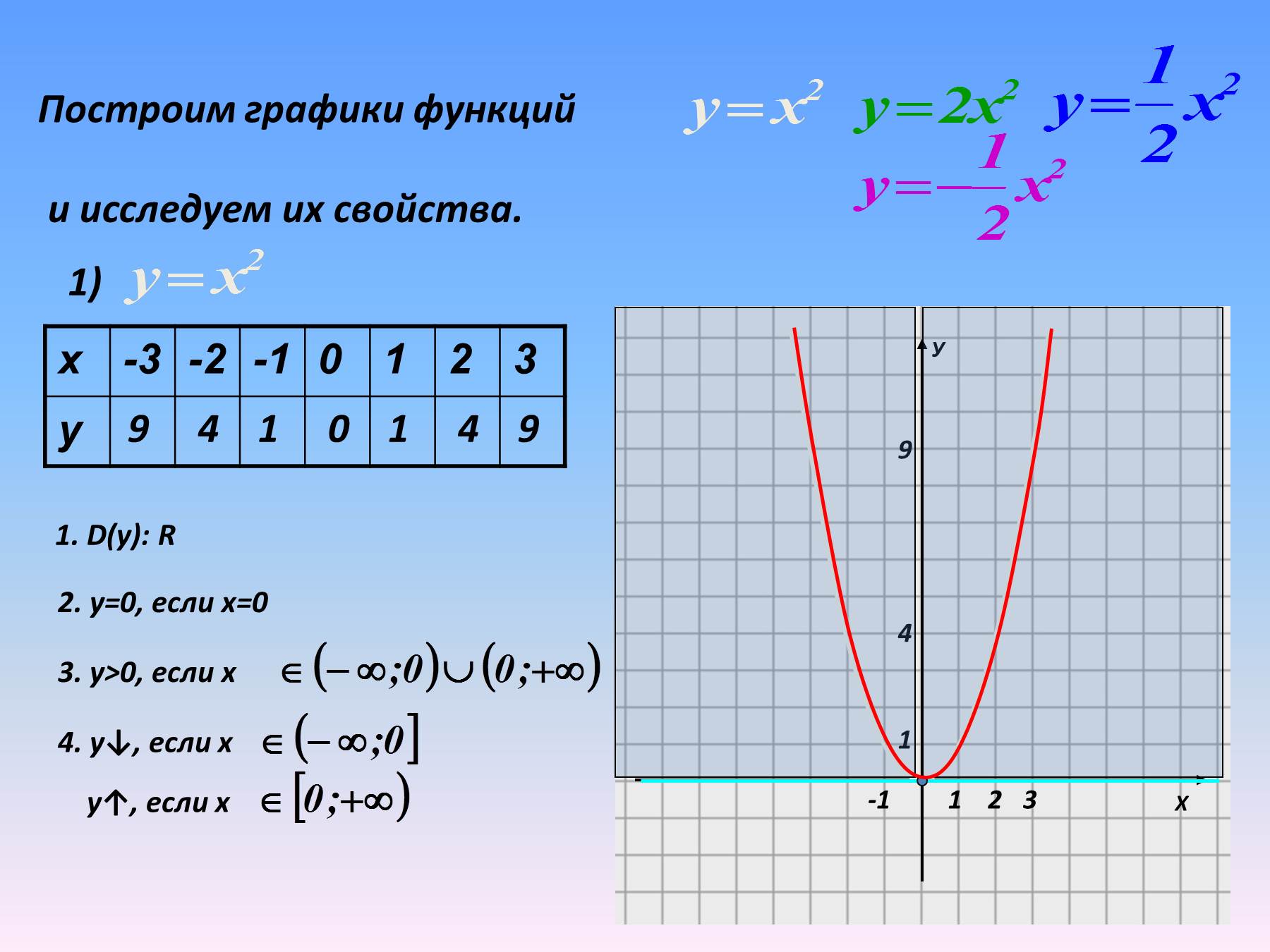
Теперь соединяем полученные точки:

Вот и все.

ОК, ну что же, теперь строить только параболы с  ?

Конечно, нет. Сейчас разберемся, что с ними делать, если  .

Рассмотрим несколько типичных случаев.

1.  .

   То есть функция выглядит как  . Ну что же здесь сложного? Просто переворачиваем параболу рогами вниз, и все.То есть, теперь будем двигаться так:

   •   вправо – вниз
   •   вправо – вниз
   •   вправо –  вниз
   • и т.д.

   

2.  .

   Что делать, если, например,  ?Все просто: начинаем так же:   вправо, но когда дело доходит до «вверх», любое число увеличиваем в   раза:

   •   вправо –   вверх
   •   вправо –   вверх
   •   вправо –   вверх
   • и т.д.

   Аналогично в случае  :

   •   вправо –   вниз
   •   вправо –   вниз
   •   вправо –   вниз
   • и т.д.

   В общем случае так:   вправо –   вверх   вправо –   вверх   вправо –   вверх и т.д.

   Если  , то вместо «вверх» делаем «вниз».

3. А если  ? Принцип тот же: каждый шаг вправо или влево сопровождается шагом вверх или вниз, равным какому-то нечетному числу, умноженному на  . Но отмерять нецелые (дробные) отрезки всегда лень. Поэтому иногда удобнее сделать по-другому: шаг вправо или влево делать не  , а  . Тогда вверх/вниз придется смещаться на целые  ,  ,  ,  , … клеток.

   Например: построим график  . Будем откладывать:

   • вправо   – вниз  
   • вправо   – вниз  
   • вправо   – вниз  

   и затем то же самое влево.

   

• Отлично, параболу рисовать научились, давай теперь потренируемся на настоящих функциях.
• Итак, нарисуй графики таких функций:
• Ответы:
• 1.  :

2.  

3. Вершина:  .

Помнишь, что делать, если старший коэффициент меньше  ?

Смотрим на знаменатель дроби: он равен  . Значит, будем двигаться так:

•   вправо –   вверх
•   вправо –   вверх
•   вправо –   вверх

и так же влево:

4. Вершина:  .

Ой, а что с этим делать? Как отмерять клетки, если вершина где-то между линиями?..

А мы схитрим. Нарисуем сперва параболу, а уже потом переместим ее вершиной в точку  . Даже нет, поступим еще хитрее: нарисуем параболу, а потом переместим оси:   – на   вверх, а  – на   вправо:

Этот прием очень удобен в случае любой параболы, запомни его.

Рассмотрим еще один способ записи квадратичной функции: выделение полного квадрата. Этот способ был подробно описан в теме «Квадратные уравнения».

1. Напомню, что мы можем представить функцию   в таком виде:
2.  .
3. Например:  .
4. Или:  .
5. Что это нам дает?
6. Дело в том, что число, которое вычитается из   в скобках ( ) – это абсцисса вершины параболы, а слагаемое за скобками ( ) – ордината вершины.
7. Это значит, что, построив параболу  , нужно будет просто сместить ось   на   влево и ось   на   вниз.
8. Пример: построим график функции  .
9. Выделим полный квадрат:
10.  .

Какое число вычитается из   в скобках? Это   (а не  , как можно решить, не подумав).

• Итак, строим параболу  :
• Теперь смещаем ось   на   вниз, то есть на   вверх:
• А теперь –   на   влево, то есть на   вправо:

Вот и все. Это то же самое, как переместить параболу   вершиной из начала координат в точку  , только прямые оси двигать намного легче, чем кривую параболу.

1. Теперь, как обычно, сам:
2. И не забывай стирать ластиком старые оси!
3. Я в качестве ответов для проверки напишу тебе ординаты вершин этих парабол:
4. Все сошлось?

Если да, то ты молодец! Уметь обращаться с параболой – очень важно и полезно, и здесь мы выяснили, что это совсем не трудно.

Построение графика квадратичной функции. коротко о главном

Квадратичная функция — функция вида  , где  ,   и   ­– любые числа (коэффициенты),   – свободный член.

График квадратичной функции — парабола.

Если коэффициент  , ветви параболы направлены вниз, если   — ветви параболы направлены вверх. Чем больше значение   (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше  , тем парабола шире.

Вершина параболы:   , т.е. чем больше b, тем левее смещается вершина параболы. Подставляем   в функцию   и получаем:  , т.е. чем b больше по модулю, тем выше будет вершина параболы

Свободный член   – это координата пересечения параболы с осью ординат.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

• Стать учеником YouClever,
• Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 
• А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

Источник: https://youclever.org/book/postroenie-grafika-kvadratichnoj-funktsii-1

Как строить графики квадратичных функций (Парабол)?

Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения.

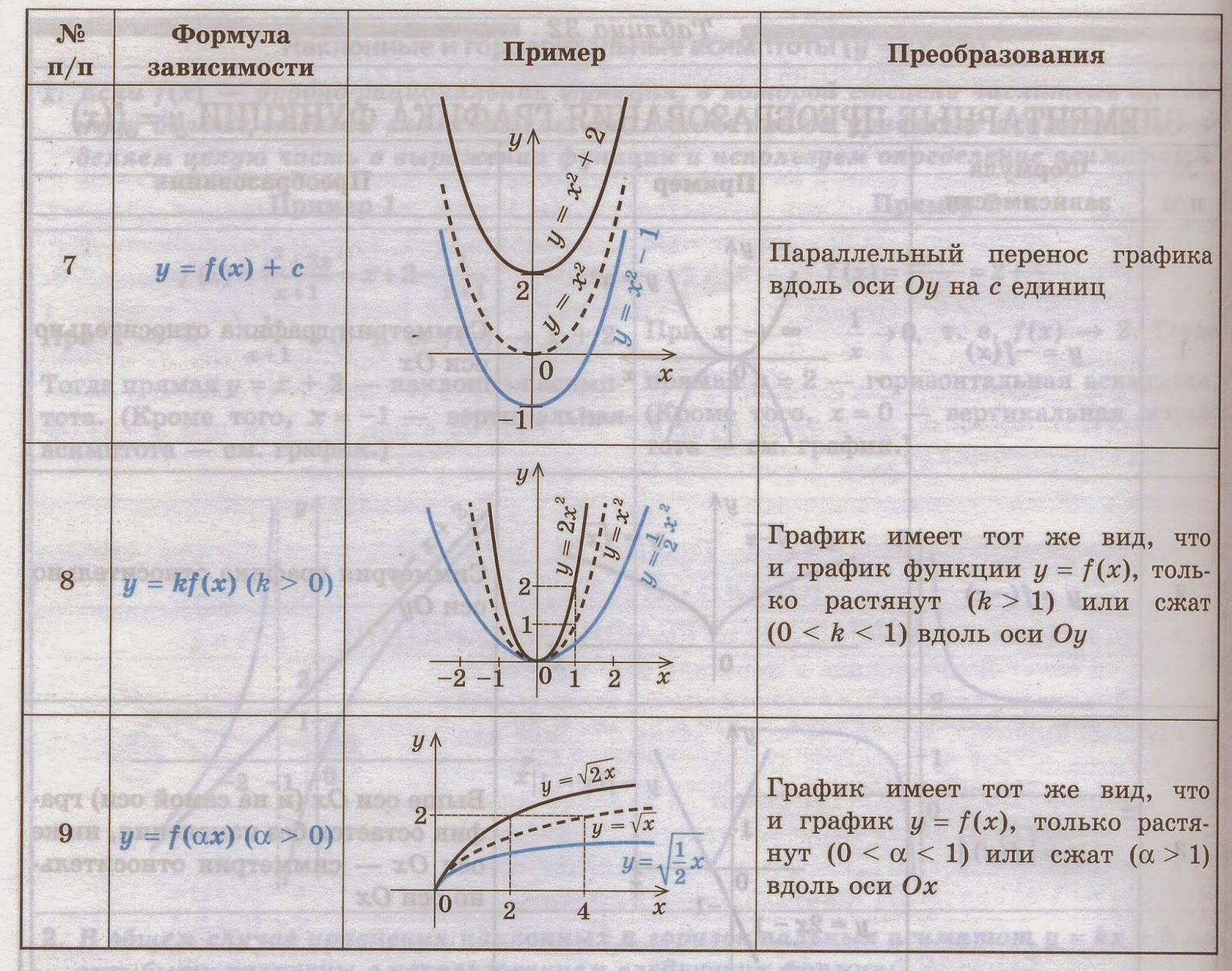
У точки в этой системе есть две координаты. M(x, y): M это название точки, x это абсцисса и она измеряется по Ox, а y это ордината и мерится по Oy.

Две координаты отображают расстояние от точки до двух осей.

• Если мы рассмотрим функцию f: A -> B (где A — область определения, B — область значений функции), тогда точку на графике данной функции можно представить в форме P(x, f(x)).
• Пример
  f:A -> B, f(x) = 3x — 1
• If x = 2 => f(2) = 3×2 — 1 = 5 => P(2, 5) ∈ Gf (где Gf это график данной функции).

Квадратичная функция

Стандартная форма: f(x) = ax2 + bx + c

Вершинная форма: $f(x)=(a+frac{b}{2a})^2-frac{Delta}{4a}$
где Δ = b2 — 4ac

Если a > 0, то минимальным значением f(x) будет $-frac{Delta}{4a}$ , которое получается, если $x=-frac{b}{2a}$.
Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-frac{b}{2a};-frac{Delta}{4a})$.

Если a < 0, то минимальное значение f(x) будет $-frac{Delta}{4a}$ , которое получается, если $x=-frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-frac{b}{2a};-frac{Delta}{4a})$.

Парабола симметрична относительно прямой, которую она пересекает $x=-frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, когда мы присваиваем знаячения x, то вибираем их симметричными относительно $-frac{b}{2a}$.
При построении графика, точки пересечения с осями координат очень важны.

|. Точка, расположенная на оси Ox имеет форму P(x, 0), потому что расстояние от неё до Ox равно 0. Если точка находиться и на Ox и на графике функции,то она также имеет вид P(x, f(x)) ⇒ f(x) = 0.

Таким образом, для того чтобы найти координаты точки пересечения с осью Ox, мы должны решить уравнение f(x)=0.
Мы получаем уравнение a2 + bx + c = 0.

1. Решение уравнения зависит от знака Δ = b2 — 4ac.
2. Иммем следующие варианты:
3. 1) Δ < 0,
   тогда у уравнения нет решений в R (множестве действительных чисел) и график не пересекает Ox. Форма графика будет:

или

2) Δ = 0,
тогда у уравнения два решения $x_1=x_2=-frac{b}{2a}$

График касается оси Ox в вершине параболы. Форма графика будет:

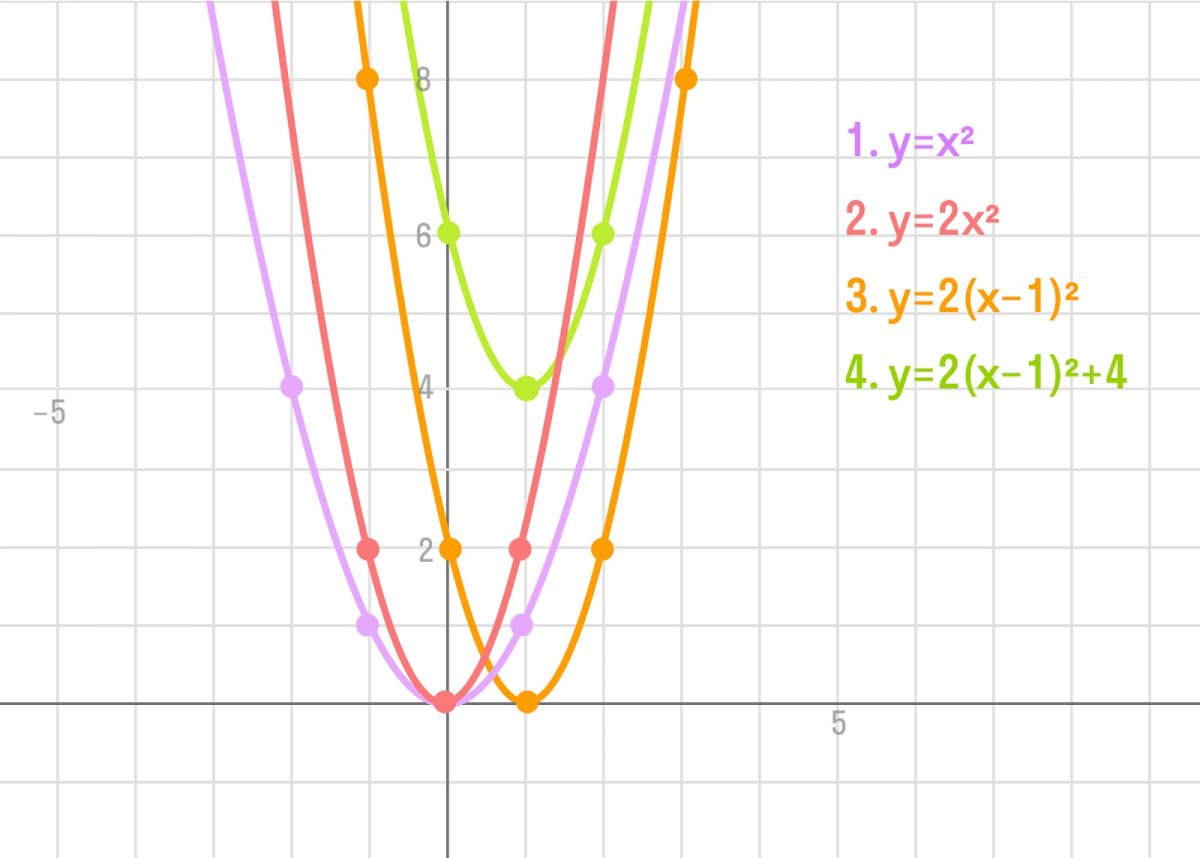
или

• 3) Δ > 0,
  тогда у уравнения два разных решения.
• $x_1=frac{-b-sqrt{Delta}}{2a}$ и
  $x_2=frac{-b+sqrt{Delta}}{2a}$
• График функции будет пересекать ось Ox в точках M(x1 и Ox. Форма графика будет:

или

||. Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).

В случае квадратичной функции,
f(0) = a×02 + b×0 + c ⇒ R(0, c).

Необходимые шаги для построения графика квадратичной функции

f: R → R
f(x) = ax2 + bx + c

1. Составляем таблицу переменных, куда заносим некоторые важные значения x.

2. Вычисляем координаты вершины$V(-frac{b}{2a};-frac{Delta}{4a})$.

3. Также записываем 0 в таблицу и нулевые значения симметричные $-frac{b}{2a}$.

или

4. Мы определяем точку пересечения с осью Ox,решая уравнение f(x)=0 и записываем корни x1 и x2 в таблице.
Δ > 0 ⇒

1. Δ < 0 ⇒ точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-frac{b}{2a}$

Δ = 0 ⇒ график касается Ox прямо в вершине параболы. Мы снова выберем два удобных значения, симметричных $-frac{b}{2a}$.
Для лучшего определения формы графика мы может выбрать другие пары значений для x, но они должны быть симметричны $-frac{b}{2a}$.

5. Мы наносим эти значения на систему координат и строим график, соединяя эти точки.

• Пример 1
  f: R → R
• f(x) = x2 — 2x — 3
• Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
• 1. $-frac{Delta}{4a}=-frac{16}{4}=-4$

a = 1, b = -2, c = -3
$-frac{b}{2a}=frac{2}{2}=1$
⇒ V(1; -4)

2. f(0) = -3
Симметричное 0 значение относительно 1 равно 2.

f(2) = -3

3. f(x) = 0 ⇒ x2 — 2x — 3 = 0
Δ = 16 > 0

1. $x_1=frac{-b-sqrt{Delta}}{2a}=frac{2-4}{2}=-1$
2. $x_1=frac{2+4}{2}=3$
3. Мы нашли точки:
   A(-1; 0)
   B(0; -3)
   V(1; -4)
   C(2; -3)
4. D(3; 0)
5. График будет иметь вид:
6. Пример 2
   f: R → R
7. f(x) = -x2 — 2x + 8
8. Δ = b2 — 4×a×c = (-2)2 — 4×(-1)×8 = 36
9. 1. $-frac{Delta}{4a}=-frac{-36}{-4}=9$
10. 2. f(0) = 8
    f(-2) = 8 (симметричное 0 значение относительно -1 равно -2)
11. 3. f(x) = 0 ⇒ -x2 — 2x + 8 = 0
    Δ = 36
12. x1 = 2 и x2 = -4
13. A(-4; 0)
    B(-2; 8)
    V(-1; 9)
    C(0; 8)
    D(2; 0)
14. Пример 3
    f: R → R
15. f(x) = x2 — 4x + 4
16. Δ = b2 — 4×a×c = (-4)2 — 4×1×4 = 0
17. 1. $-frac{Delta}{4a}=0$
18. 2. f(0) = 4
    f(4) = 4 (симметричное 0 значение относительно 2 равно 4)
19. 3. f(x) = 0 ⇒ x2 — 4x + 4 = 0
    Δ = 0
20. x1 = x2 = $-frac{b}{2a}$ = 2
21. A(-2; 9)
    B(0; 4)
    V(2; 0)
    C(4; 4)
    D(5; 9)
22. Пример 4
    f: R → R
23. f(x) = -x2 + 4x — 5
24. Δ = b2 — 4×a×c = 42 — 4×(-1)×(-5) = 16 — 20 = -4
25. 1. $-frac{Delta}{4a}=-frac{-4}{-4}=-1$
26. 2. f(0) = -5
    f(4) = -5 (симметричное 0 значение относительно 2 равно 4)

a = -1, b = -2, c = 8
$-frac{b}{2a}=frac{2}{-2}=-1$
⇒ V(-1; 9)

a = 1, b = -4, c = 4
$-frac{b}{2a}=frac{4}{2}=2$
⇒ V(2; 0)

a = -1, b = 4, c = -5
$-frac{b}{2a}=frac{-4}{-2}=2$
⇒ V(2; -1)

3. f(x) = 0 ⇒ -x2 + 4x — 5 = 0,
Δ < 0 У этого уравнения нет решений. Мы выбрали симметричные значения вокруг 2

• A(-1; -10)
  B(0; 5)
  V(2; -1)
  C(4; -5)
  D(5; -10)

Если область определения не R (множество действительных чисел), а какой-то интервал, то мы стираем часть графика, которая соответствует тем значениям x, которые не находятся в данном интервале. Необходимо записать конечные точки интервала в таблице.

1. Пример 5
   f: [0; +∞) → R
2. f(x) = x2 — 2x — 3
3. Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
4. 1. $-frac{Delta}{4a}=-4$
5. 2. f(0) = -3
   f(2) = -3 симметричное 0 значение относительно 1 равно 2)
6. 3. f(x) = 0 ⇒ x2 — 2x — 3 = 0,
   Δ = 16
   x1 = -1 ∉ [0; ∞)
   x2 = 3
7. A(0; -3)
   V(1; -4)
   B(2; -3)
   C(3; 0)

a = 1, b = -2, c = -3
$-frac{b}{2a}=1$
⇒ V(1; -4)

Источник: https://www.math10.com/ru/algebra/parabola.html

Как построить параболу

Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.

Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле

для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².

• Пример.
• Построить график функции y=x²+2x-3.
• Решение:

y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

   

   

От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).

y=x²+2x-3

  График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².

1. Пример.
2. Построить график функции y= -x²+2x+8.   
3. Решение:

y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

   

   

От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):

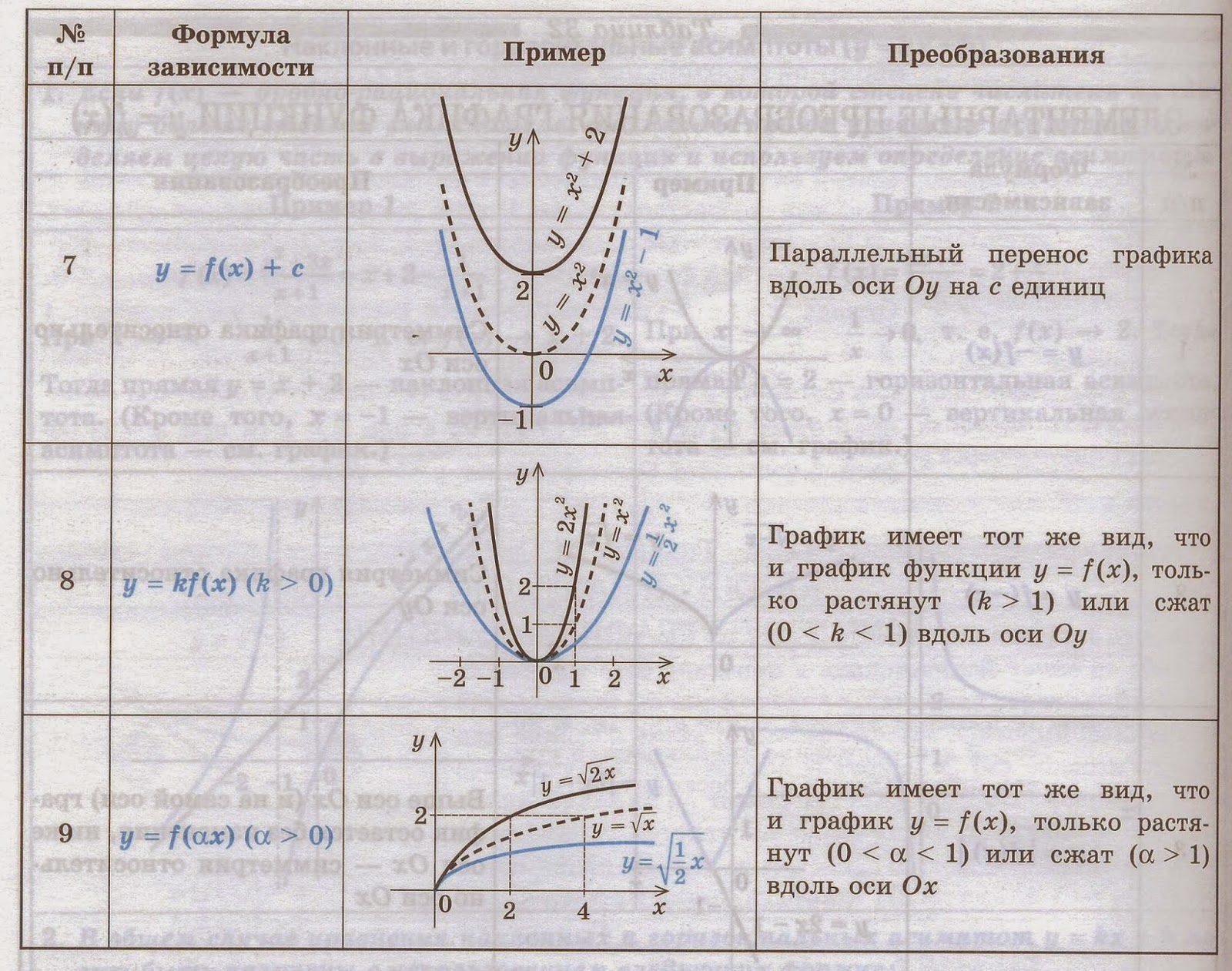
y= -x²+2x+8

Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы  умеете строить графики функций y=x² и y= -x².

Недостаток: если координаты вершины — дробные числа, строить график не очень удобно.

Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.

Другой способ построения параболы —  по точкам, то есть можно найти  несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.

• Примеры.
• Построить график функции y=x²+5x+4.
• Решение:

y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

1.    
2.    
3. то есть вершина параболы — точка (-2,5; -2,25).

Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).

В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).

Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:

y=x²+5x+4

Построить график функции y= -x²-3x.

Решение:

y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

•    
• Вершина (-1,5; 2,25) — первая точка параболы.

В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также  точкой пересечения параболы с осью ординат.

При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.

y= -x²-3x

Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.

Источник: http://www.algebraclass.ru/kak-postroit-parabolu/

Квадратичная функция — формула, свойства и виды графиков

Раздел «Квадратичная функция», ее свойства и график проходят в средней школе в 8 — 9 классах. Но не все учителя объясняют доступно. А вышедшим из ученического возраста может понадобиться обновить познания. 

Поэтому рассмотрим простые примеры построения графиков квадратичной функции.

Определение и формула квадратичной функции

Квадратичной называют функцию канонического вида:

• a, b – коэффициенты;
• с – свободный член.

Формально конструкция именуется «квадратный трехчлен». Сразу заметно, что область определения не ограничена, а четность не выявлена.

Примеры построения парабол

Займемся упрощенными случаями и подметим закономерности.

График функции при а = 1, b = c = 0

Наиболее тривиальная, но наглядная и информативная разновидность с формулой:

y = x2

Функция четная, возрастающая. Построим по точкам.

Получившаяся кривая называется «парабола». Характерна для уравнений с «квадратом».

Нижнюю точку с координатами (0; 0) называют «вершиной». Единственное место, где одной функции соответствует один аргумент. В данном случае – это минимум функции.

Уходящие вверх части кривой – «ветви». На всех участках кроме вершины к одному (y) относятся сразу (±x).

Вывод: ветви данной параболы имеют ось симметрии — вертикальную прямую ординат Y.

График функции, когда b = c = 0, а > 1 и а < 1

• Кривая задается, например, так:
• y = 2×2
• Ветви «сожмутся» относительно оси симметрии.

1. Построим другой график.
2. y = 0,5×2
3. Ветви «разойдутся».

• Куда интереснее переместить коэффициент a в отрицательную область.
• y = -x2

Парабола «повернется» на 180°. И вершина станет максимумом.

График функции при b = 0, с ≠0

1. Рассмотрим такой вариант:
2. y = x2 + 1
3. Вершина сдвинется на величину c по оси Y.

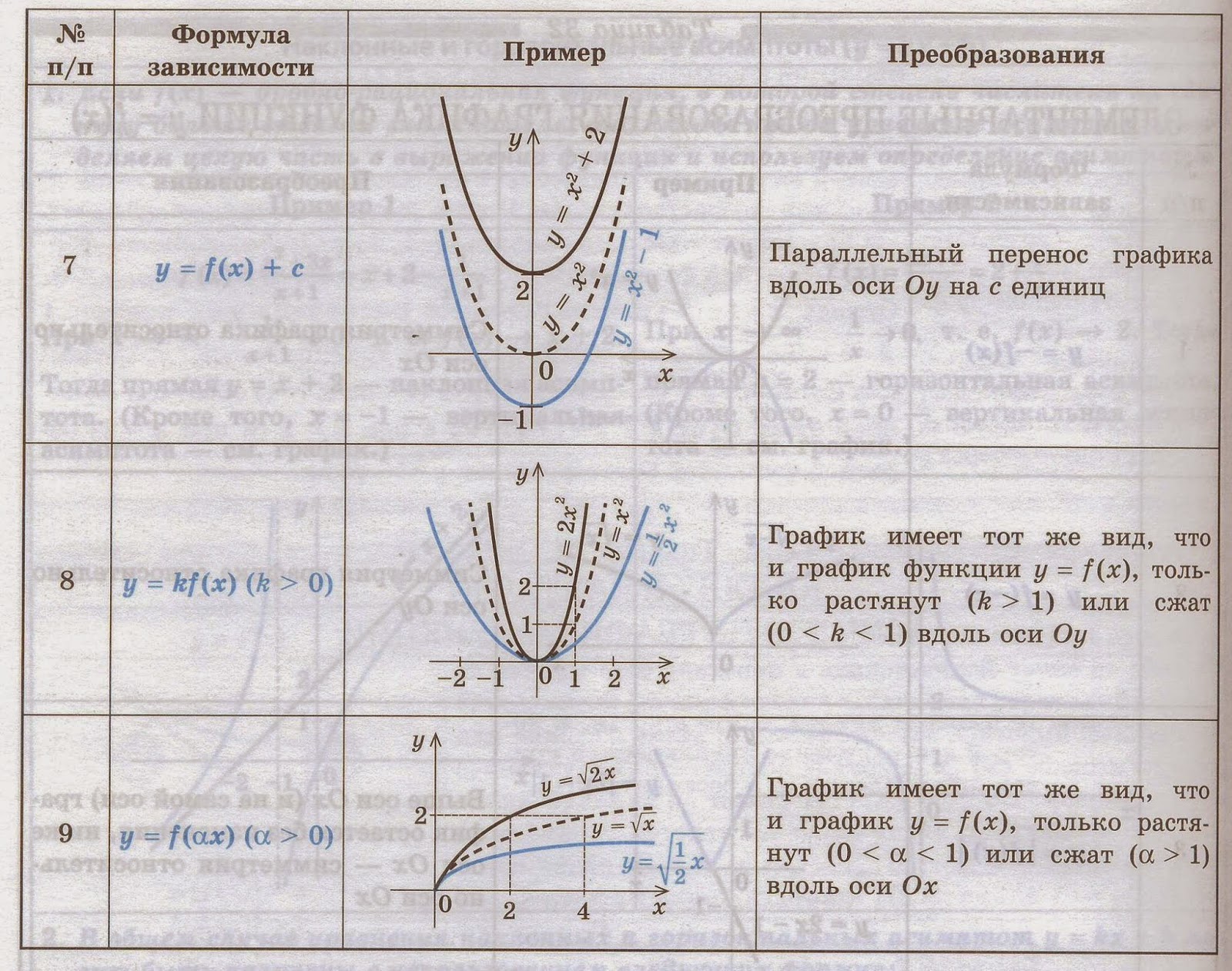
• А если параметр c отрицателен? Уравнение выглядит так:
• y = x2 — 1
• Смещение произойдет ниже точки (0; 0).

Общий случай a ≠0, b ≠0, c ≠0

Попробуем найти характерные точки.

Пересечения с осью абсцисс (y = 0)

1. Иными словами, следует решить уравнение:
2. ax2 + bx + c = 0
3. Корнями уравнения будут:

Подкоренное выражение называется «дискриминант» и обозначается «D». Появляются варианты:

1. D отрицателен, D > 0. В таком случае действительные корни не существуют. Парабола не пересекает ось Х.

2. D положителен, D > 0. Существуют оба корня. Кривая пересекает X в двух известных местах.

3. D = 0. Корень один – -b/2a. Пересечение единственно. А такое возможно в одном случае: найденное означает абсциссу вершины.

Вершина

Горизонтальная координата вычисляется по формуле:

• Вертикальная:

Касательная в вершине параболы совпадает с осью X или параллельна ей. Значит тангенс её относительного наклона равен 0. А это производная функции:

Нашли x0, а y0 находится подстановкой в уравнение найденного.

Ось симметрии

Параллельная оси ординат прямая x = x0.

Приблизительный вид

По уравнению можно прикинуть общую картину:

• положительное значение коэффициента a говорит о направленности ветвей вверх и наоборот;
• по дискриминанту определим расположение относительно X;
• находим пересечения (если есть).

Пример построения графика

1. Дано:
2. y = x2 + 2x — 3
3. Проанализируем:

• a = 1, положительный, поэтому ветви параболы направлены вверх;
• b = 2;
• с = -3.

• Алгоритм построения графика квадратичной функции:
• 1. Находим вершину:

1. 2. Определяем точки пересечения с осью X:

3. Посчитав еще 2 — 3 точки правее и левее оси симметрии x = -1, получим достоверный график.

 

Свойства параболы

Основные свойства следующие:

1. Область определения – все действительные числа.

2. Вершина является минимумом при положительном коэффициенте x2, максимумом – при отрицательном.

3. Координаты вершины зависят только от коэффициентов.

4. Ось симметрии проходит через вершину и параллельна оси ординат.

Заключение

В интернете существует масса онлайн-калькуляторов для облегчения работы с кривой. Приведенные же приемы и перечисленные свойства позволяют лучше понять сущность квадратичного выражения.

Параболические отражатели позволяют получать параллельный пучок света от точечного источника. Антенна такого типа позволяет концентрировать и усиливать радиосигнал. Не абстрактная линия на бумаге.

Источник: https://nauka.club/matematika/algebra/kvadratichnaya-funktsiya.html

Построение графика квадратичной функции

«Построение графика квадратичной функции» (9 класс)

Урок 2

Цели урока:

• Образовательные: научиться построению графика квадратичной функции и использованию графика для получения её свойств.
• Развивающие: развивать логическое мышление, алгоритмическую культуру, внимание, навыки самостоятельной работы с источником информации и самоконтроля, поддерживать интерес к математике.
• Воспитательные: воспитывать последовательность, ответственность, самостоятельность, настойчивость, дисциплинированность.

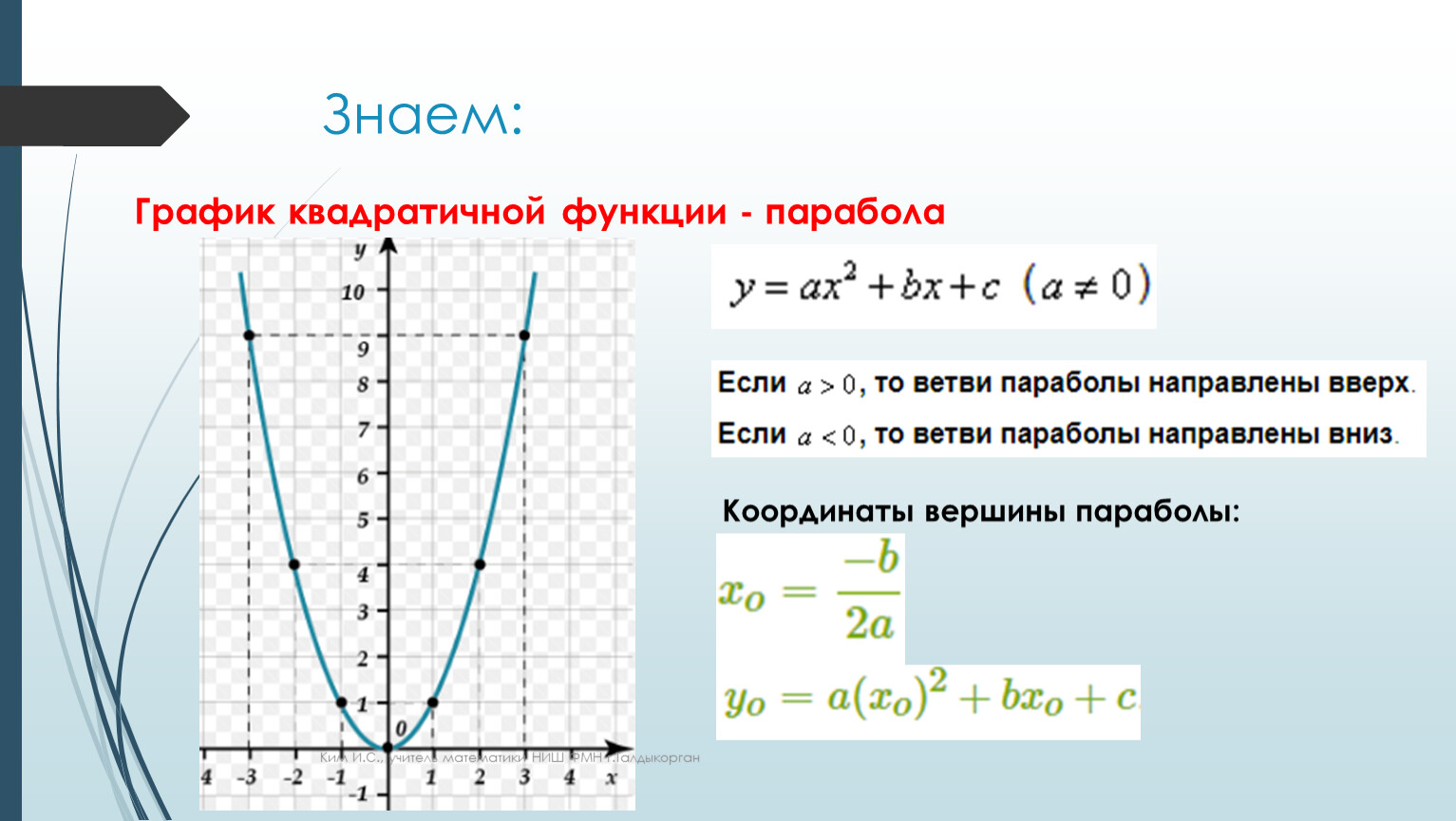
• Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c , где х — независимая переменная, a, b и с -некоторые числа (причём а≠0).
• Например: у = 5х²+6х+3,
• у = -7х²+8х-2,
• у = 0,8х²+5,
• у = ¾х²-8х,
• у = -12х²
• — квадратичные функции

0) или вниз (если ау= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ). Например: у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а у 0 х у 0 х » width=»640″

Графиком квадратичной функции является парабола , ветви которой направлены вверх (если а0) или вниз (если а

• у= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ).

Например:

• у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а

1. у
2. 0
3. х
4. у
5. 0
6. х

0) » width=»640″

• Чтобы построить график функции надо:
• 1. Описать функцию:
• название функции,
• что является графиком функции,
• куда направлены ветви параболы.

Пример: у = х ²-2х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т.к. а=1, а0)

1. Чтобы построить график функции надо:
2. Пример: у = х ²-2х-3 (а = 1; b = -2; с = -3) Найдём координаты вершины параболы
3. n = 1²-2·1-3 = -4
4. А(1;-4) – вершина параболы.
5. х=1 – ось симметрии параболы.
6. 2. Найти координаты вершины параболы А( m;n) по формулам:
7. ;

или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.

Прямая x=m является ось ю симметрии параболы.

Чтобы построить график функции надо:

3. Заполнить таблицу значений функции:

Прямая x=m является осью симметрии параболы, т.е. точки графика симметричны относительно этой прямой.

• В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. Например, следующим образом:
• *- посчитать значение функции в выбранных значениях х.
• Пример: у = х ²-2х-3
• А(1;- 4) – вершина параболы
• х=1 – ось симметрии параболы.
• Составим таблицу значений функции:
• Х
• у
• — 1
• 0
• 0
• — 3
• 1
• — 4
• 2
• — 3
• 3
• 0
• Х
• у
• m-2
• *
• m-1
• *
• m
• m+1
• n
• *
• m+2
• *

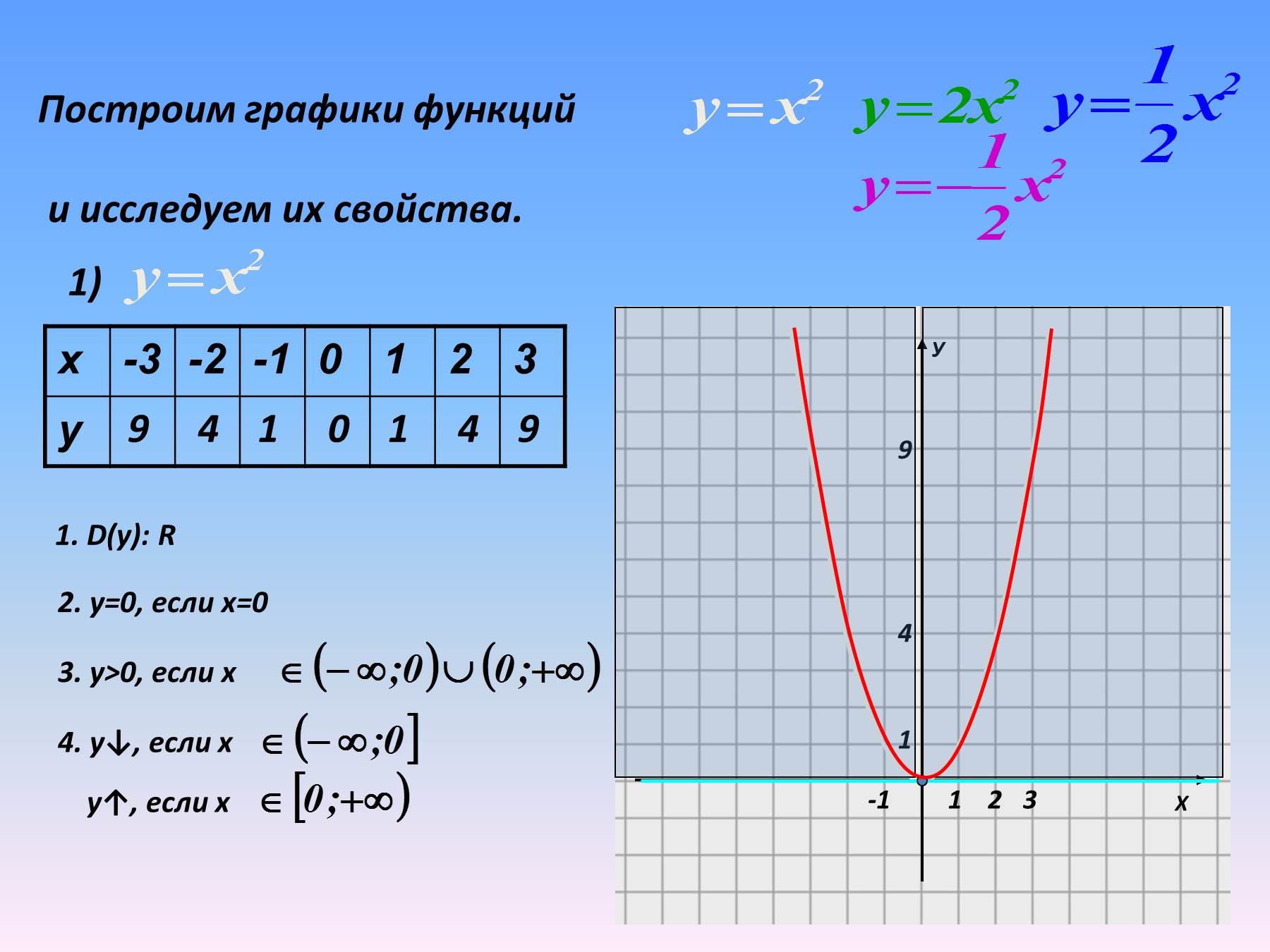
Чтобы построить график функции надо:

4. Построить график функции: — отметить в координатной плоскости точки, координаты которых указаны в таблице; — соединить их плавной линией.

1. х
2. у
3. -1
4. 0
5. 0
6. -3
7. 1
8. -4
9. 2
10. -3
11. 3
12. 0
13. У
14. 4
15. -4
16. 3
17. -3
18. 2
19. -2
20. 1
21. -1
22. у = х ²-2х-3
23. 0
24. -2
25. 1
26. -1
27. -3
28. 2
29. 3
30. -4
31. 4
32. -5
33. 5
34. 6
35. х

Попробуйте ответить на контрольные вопросы:

• Сформулируйте определение квадратичной функции.
• Что представляет собой график квадратичной функции?
• Куда могут быть направлены ветви параболы и от чего это зависит?
• В какой последовательности нужно строить график квадратичной функции?

• Стоит немного отдохнуть от компьютера.
• Попробуйте построить в тетради график функции
• у = -2х²+8х-3

Постройте график функции у = -2х ²+8х-3 План построения графика квадратичной функции:

1. Описать функцию:

• название функции; что является графиком функции; куда направлены ветви параболы
• название функции;
• что является графиком функции;
• куда направлены ветви параболы

1. 2. Найти координаты вершины параболы А( m;n)
2. по формулам:
3. или n = у(m)

3. Заполнить таблицу значений функции.

4. Построить график функции:

• отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.
• отметить в координатной плоскости точки, координаты которых указаны в таблице;
• соединить их плавной линией.

Проверьте себя. Ваше задание должно быть выполнено следующим образом:

у = -2х ²+8х-3 — квадратичная функция, графиком является парабола, ветви которой направлены вниз (т.к. а=-2, а

• Найдём координаты вершины параболы
• n = -2·2²+8·2-3 =5
• А ( 2; 5 ) – вершина параболы.
• х=5 ось симметрии параболы.
• Составим таблицу значений функции.
• у = -2х ²+8х-3
• у
• 7
• 6
• 5
• 4
• -3
• 3
• -2
• 2
• -1
• 1
• 0
• -1
• 1
• -2
• -3
• 2
• 3
• -4
• 4
• 5
• 6
• х
• Х
• у
• 0
• -3
• 1
• 3
• 2
• 3
• 5
• 3
• 4
• -3

Если у вас получилось тоже самое – вы молодец и мы вас поздравляем!!! Вы можете перейти к следующей странице .

Если вы допустили ошибку – не огорчайтесь. У вас всё ещё впереди! Вы можете заглянуть в свой учебник (п.7)

0 на промежутке (0,5;3,5) y Функция возрастает на промежутке (-∞;2] функция убывает на промежутке [2;+∞) Наибольшее значение функции равно 5 у 7 6 5 4 3 у = -2х ²+8х-3 2 -1 1 0 -2 1 -1 2 -3 3 -4 4 х » width=»640″

Рассмотрим свойства этой квадратичной функции. (листаем свойства по щелчку мыши)

• Область определения функции (-∞;+∞)

Область значений функции (-∞;5]

• Нули функции х =0,5 и х =3,5
• у 0 на промежутке (0,5;3,5)

y

• Функция возрастает на промежутке (-∞;2]

функция убывает на промежутке [2;+∞)

• Наибольшее значение функции равно 5

1. у
2. 7
3. 6
4. 5
5. 4
6. 3
7. у = -2х ²+8х-3
8. 2
9. -1
10. 1
11. 0
12. -2
13. 1
14. -1
15. 2
16. -3
17. 3
18. -4
19. 4
20. х

• Перед продолжением работы запишите домашнее задание,
• № 122, 124(а),
• 244(б,в)
• Далее выполните тест.

• прочитайте задание;
• выполните его устно или, сделав записи в тетради;
• и выберите правильный ответ

1. Выполните тест
2. 1 вопрос: Выберите квадратичную функцию а)
3. б)
4. в)
5. г)

Выполните тест

2 вопрос: Куда направлены ветви параболы ?

• Выполните
• 3 вопрос: Укажите координаты вершины параболы
• а) А(3;6)
• б) А(-1;-17)
• в) А(1;-5)
• г) А(1;-1)

1. Выполните тест
2. у
3. У
4. У
5. 0 6
6. х
7. -6 0
8. х
9. -6 0
10. х
11. 4 вопрос:
12. На рисунке показаны графики квадратичных функций. Выберите график функции
13. у= — 4х²-16х+1, подведите к нему стрелку и нажмите левую кнопку мыши .
14. у
15. у
16. 17
17. 5
18. у
19. 1
20. 0 2,5
21. х
22. -2 х
23. 2,5
24. 6
25. 0
26. х

Выполните тест

5 вопрос: Укажите формулу квадратичной функции, график которой изображён на рисунке.

• у = -x 2 +6x
• у = — 3х²+8х-11
• у = — 4х²-16х+1
• у = х²-6х
• у = х²+6х
• у = 1,2х²-6х+5

• У
• -6 0
• х

1. Выполните следующую работу в тетрадях по вариантам. Постройте графики функций:
2. у = -х ²+6х-8
3. Укажите свойства функции.
4. у = х ²-6х-7
5. Укажите свойства функции.

Источник: https://multiurok.ru/index.php/files/postroenie-grafika-kvadratichnoi-funktsii-2.html