- [{Large{ ext{Подобие треугольников}}}]
- Определения
- Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого(стороны называются сходственными, если они лежат напротив равных углов).
- Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

- Определение
- Периметр треугольника – это сумма длин всех его сторон.
- Теорема
- Отношение периметров двух подобных треугольников равно коэффициенту подобия.
- Доказательство
Рассмотрим треугольники (ABC) и (A_1B_1C_1) со сторонами (a,b,c) и (a_1, b_1, c_1) соответственно (см. рисунок выше).
- Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1}) - Теорема
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
- Доказательство
Пусть треугольники (ABC) и (A_1B_1C_1) подобны, причём (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = dfrac{BC}{B_1C_1} = k). Обозначим буквами (S) и (S_1) площади этих треугольников соответственно.

- Так как (angle A = angle A_1), то (dfrac{S}{S_1} = dfrac{ABcdot
AC}{A_1B_1cdot A_1C_1}) (по теореме об отношении площадей треугольников, имеющих по равному углу). - Так как (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = k), то (dfrac{S}{S_1} = dfrac{AB}{A_1B_1}cdotdfrac{AC}{A_1C_1} = kcdot k = k^2), что и требовалось доказать.
- [{Large{ ext{Признаки подобия треугольников}}}]
- Теорема (первый признак подобия треугольников)
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Доказательство
Пусть (ABC) и (A_1B_1C_1) – треугольники такие, что (angle A =
angle A_1), (angle B = angle B_1). Тогда по теореме о сумме углов треугольника (angle C = 180^circ — angle A — angle B = 180^circ
— angle A_1 — angle B_1 = angle C_1), то есть углы треугольника (ABC) соответственно равны углам треугольника (A_1B_1C_1).

- Так как (angle A = angle A_1) и (angle B = angle B_1), то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1}) и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1}). - Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1}). - Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1}) (используя равенства (angle B = angle B_1), (angle C = angle C_1)). - В итоге, стороны треугольника (ABC) пропорциональны сходственным сторонам треугольника (A_1B_1C_1), что и требовалось доказать.
- Теорема (второй признак подобия треугольников)
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
- Доказательство
Рассмотрим два треугольника (ABC) и (A'B'C'), таких что (dfrac{AB}{A'B'}=dfrac{AC}{A'C'}), (angle BAC = angle A'). Докажем, что треугольники (ABC) и (A'B'C') – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B').

Рассмотрим треугольник (ABC''), у которого (angle 1 = angle A'), (angle 2 = angle B'). Треугольники (ABC'') и (A'B'C') подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A'B'} =
dfrac{AC''}{A'C'}).
С другой стороны, по условию (dfrac{AB}{A'B'} = dfrac{AC}{A'C'}). Из последних двух равенств следует, что (AC = AC'').
- Треугольники (ABC) и (ABC'') равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B').
- Теорема (третий признак подобия треугольников)
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
- Доказательство
Пусть стороны треугольников (ABC) и (A'B'C') пропорциональны: (dfrac{AB}{A'B'} = dfrac{AC}{A'C'} = dfrac{BC}{B'C'}). Докажем, что треугольники (ABC) и (A'B'C') подобны.

- Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A').
- Рассмотрим треугольник (ABC''), у которого (angle 1 = angle A'), (angle 2 = angle B').
- Треугольники (ABC'') и (A'B'C') подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A'B'} = dfrac{BC''}{B'C'}
= dfrac{C''A}{C'A'}). - Из последней цепочки равенств и условия (dfrac{AB}{A'B'} =
dfrac{AC}{A'C'} = dfrac{BC}{B'C'}) вытекает, что (BC = BC''), (CA
=
C''A). - Треугольники (ABC) и (ABC'') равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A').
![]()
- [{Large{ ext{Теорема Фалеса}}}]
- Теорема
- Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
- Доказательство
- Докажем сначала лемму: Если в ( riangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1), то она пересечет сторону (OB_1) также в середине.

Через точку (B_1) проведем (lparallel OB). Пусть (lcap a=K). Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle
A_1KB_1=angle ABB_1=angle OAA_1); (angle AA_1O=angle KA_1B_1) как вертикальные. Значит, по второму признаку ( riangle
OAA_1= riangle B_1KA_1 Rightarrow OA_1=A_1B_1). Лемма доказана.

Перейдем к доказательству теоремы. Пусть (OA=AB=BC), (aparallel
bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1).
Таким образом, по данной лемме (OA_1=A_1B_1). Докажем, что (A_1B_1=B_1C_1). Проведем через точку (B_1) прямую (dparallel OC), причем пусть (dcap a=D_1, dcap c=D_2).
Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2).
Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2) как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1) как накрест лежащие, и, значит, по второму признаку ( riangle A_1B_1D_1= riangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1).
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d). Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно, где (k) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1) прямую (pparallel OD) ((ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2)). Тогда ( riangle OAA_1
sim riangle A_1B_1B_2) по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb).
Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow
riangle OBB_1sim riangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.
![]()
- [{Large{ ext{Средняя линия треугольника}}}]
- Определение
- Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
- Теорема
- Средняя линия треугольника параллельна третьей стороне и равна ее половине.
- Доказательство
- 1) Параллельность средней линию основанию следует из доказанной выше леммы.
- 2) Докажем, что (MN=dfrac12 AC).
Через точку (N) проведем прямую параллельно (AB). Пусть эта прямая пересекла сторону (AC) в точке (K). Тогда (AMNK) — параллелограмм ((AMparallel NK, MNparallel AK) по предыдущему пункту). Значит, (MN=AK).
Т.к. (NKparallel AB) и (N) – середина (BC), то по теореме Фалеса (K) – середина (AC). Следовательно, (MN=AK=KC=dfrac12 AC).
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12).
Источник: https://shkolkovo.net/theory/55
Матвокс ⋆ признак средней линии треугольника ⋆ энциклопедия математики
Skip to content
Если отрезок параллелен одной из сторон треугольника и соединяет середину одной стороны треугольника с точкой, лежащей на другой стороне треугольника, то это средняя линия треугольника.

Признак средней линии треугольника
Рассмотрим треугольник АВС.
Пусть точка К делит сторону АВ пополам:
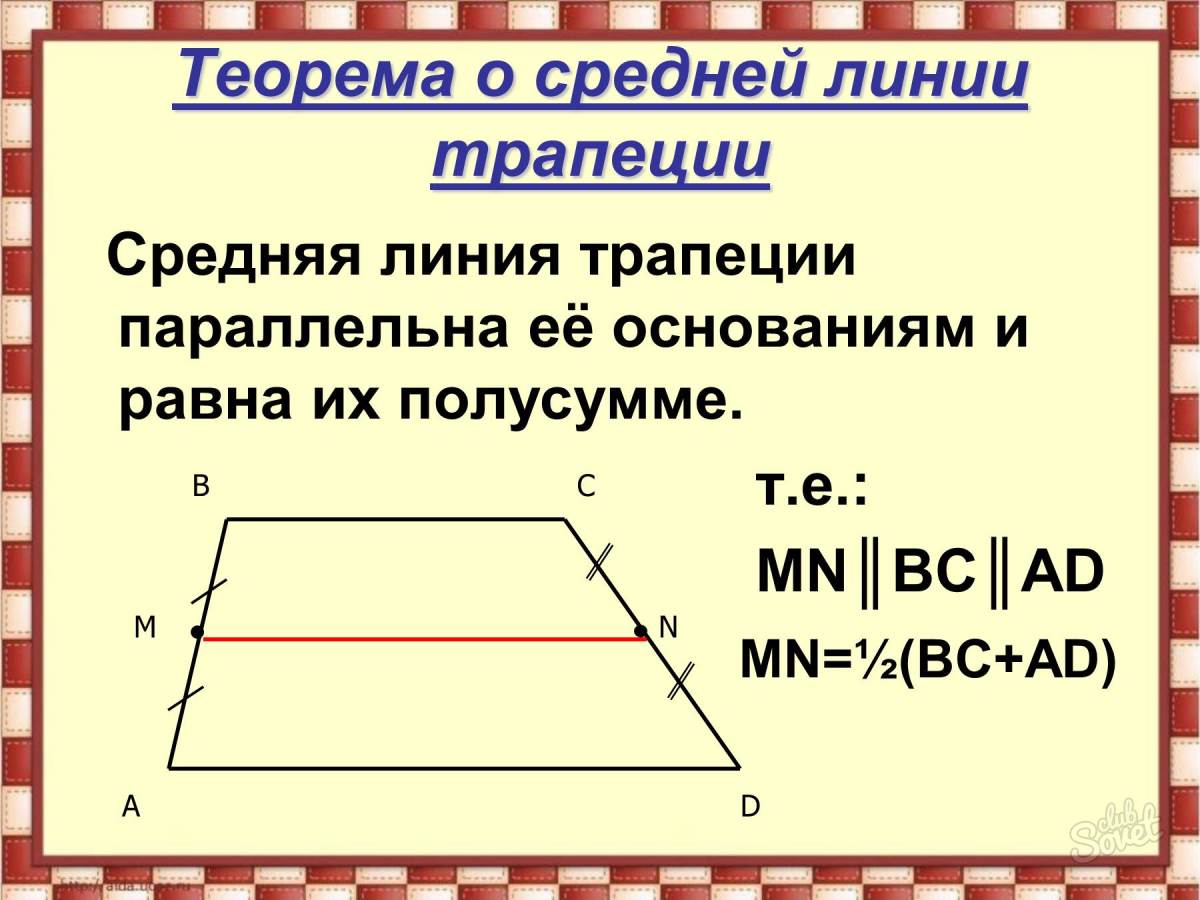
И пусть через точку К проходит отрезок КЕ, параллельный стороне треугольника АС:

Докажем, что КЕ – средняя линия треугольника, т.е. докажем, что:


Доказательство признака средней линии треугольника. Шаг 1
Так как KE||AC и АК=КВ, то по теореме Фалеса если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Следовательно:

Признак средней линии треугольника доказан.

Доказательство признака средней линии треугольника. Шаг 2
MATHVOX
Go to Top
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Источник: https://mathvox.ru/geometria/treugolniki/treugolniki-glava-12/priznak-srednei-linii-treugolnika/
Замечательные линии треугольника
Медиана треугольника – это отрезок, который связывает вершину треугольника с серединой одной из сторон данного треугольника.
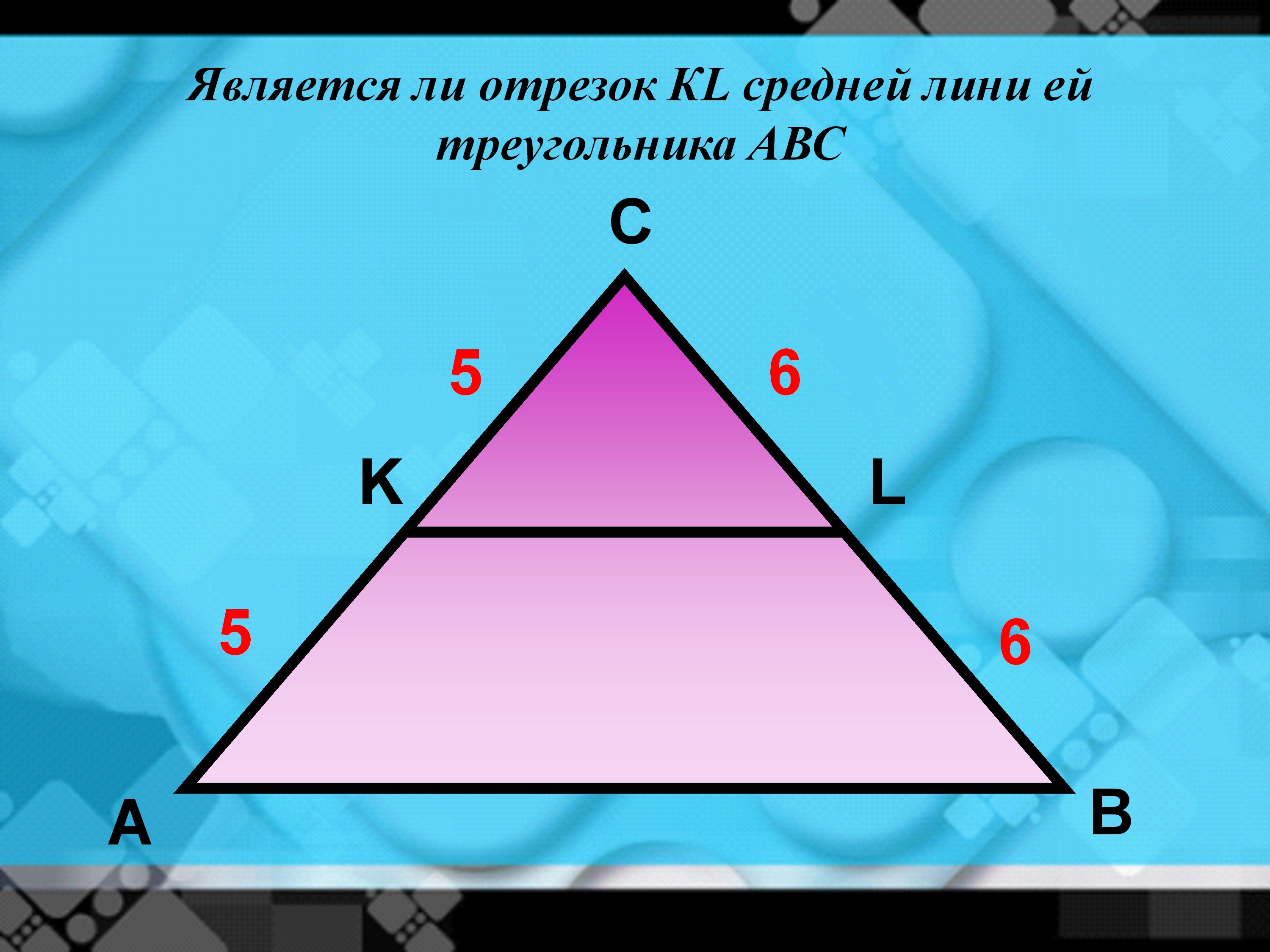
Медиана треугольника
Медиана делит треугольник на два треугольника, площади которых одинаковы.
Медианы треугольника пересекаются только в одной точке, которая разделяет каждую из них в отношении 2 : 1, отсчитывая от вершины. Такая точка именуется центром тяжести треугольника.
Весь треугольник разбивается своими медианами на шесть равных по значению треугольников.
Биссектриса угла – это исходящий из вершины угла луч, пролегающий между образующими сторонами и разделяющий его пополам.

Свойства биссектрисы треугольника
- Биссектриса угла – есть геометрическое место точек, которые равноудалены от сторон этого угла.
- Биссектриса угла треугольника, разделяет противолежащую сторону на отдельные отрезки, которые пропорциональны прилежащим сторонам:
- В точке, где пересекаются биссектрисы треугольника, находится центр окружности, который вписан в этот треугольник.
Высотой треугольника называется линия, проведенная из вершины треугольника к одной из сторон расположенной перпендикулярно.

Свойства высоты треугольника
Перпендикулярная линия высоты прямоугольного треугольника разделяет его на два подобных ему треугольника.
Две линии высоты остроугольного треугольника, отделяют от него подобные треугольники.
Перпендикулярная прямая, которая проходит через середину отрезка, называется – срединный перпендикуляр к отрезку.

Срединный перпендикуляр
Все точки серединного перпендикуляра к отрезку равноудалены от окончаний этого отрезка. Верно так же и обратное утверждение, что каждая точка, находящаяся на равных расстояниях от концов отрезка, расположена на серединном перпендикуляре к нему.
В точке пересечения серединных перпендикуляров, проведенных в направлении к одной из сторон треугольника, находится центр окружности, который описывает данный треугольник.
Отрезок, который соединяет две стороны треугольника в их серединах, называется – средняя линия треугольника.

Средняя линия
Средняя линия, какого либо треугольника, всегда расположена параллельно одной из его сторон и является половиной этой стороны.
Источник: http://simple-math.ru/geometry/line-triangle.php
Длина средней линии треугольника
Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для казалось бы сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.

Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от углов треугольники делятся на:
- Остроугольные
- Тупоугольные
- Прямоугольные
Рис. 1. Виды треугольников
Основными характеризующими отрезками треугольника являются:
- Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
- Биссектриса – отрезок, делящий угол пополам
- Высота – перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Рис. 2. Высота, медиана и биссектриса в треугольнике
Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.
Однако существует и ряд дополнительных характеризующих отрезков:
- Серединный перпендикуляр – высота восстановленная из середины высоты. Как правило серединный перпендикуляр продолжается до пересечения с другой стороной.
- Средняя линия – отрезок, соединяющий середины смежных сторон.
- Радиус вписанной окружности. Вписанная окружность – окружность, которая касается каждой из сторон треугольника.
- Радиус описанной окружности. Описанная окружность – окружность, содержащая в себе все стороны треугольника.
Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.
Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.
Поэтому приведем и обсудим все свойства средней линии треугольника:
- Средняя линия равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
- Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в прошлом свойстве.
- Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
- Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5

Рис. 3. Средние линии в треугольнике
Собственно формула длины средней линии вытекает из второго свойства:
$m=1over{2}*a$- где m – средняя линия, а- сторона противоположная средней линии.
Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили о особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.
Средняя оценка: 4.3. Всего получено оценок: 185.
Источник: https://obrazovaka.ru/geometriya/dlina-sredney-linii-treugolnika-formula.html
Как находить среднюю линию треугольника? Основные свойства, определения и способы :
Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.
Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.
Как находить среднюю линию треугольника? Давайте разбираться.
Основные понятия
Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.
Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.
Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.
Свойства
Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.
- Средняя линия параллельна стороне данной геометрической фигуры и равна ее 1/2. Это говорит о том, что если, к примеру, сторона равна 8, то средняя линия будет равна 4.
- Проводя в данной геометрической фигуре всевозможные средние линии, мы получим 4 треугольника, равных и подобных друг другу. Также их коэффициент подобия будет равен 1/2.

- И последнее свойство о том, что одна проведенная средняя линия делит основной треугольник на трапецию и треугольник.
Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.
Приведем пример

Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.
Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.
Источник: https://www.syl.ru/article/286665/new_kak-nahodit-srednyuyu-liniyu-treugolnika-osnovnyie-svoystva-opredeleniya-i-sposobyi
Президентский ФМЛ №239
math-public:srednyaya_liniya_treugolnika
Отрезок, соединяющий середины двух сторон треугольника, называется
средней линией треугольника.
Средняя линия треугольника параллельна стороне треугольника и равна
ее половине.
- Рассмотрим $ riangle ABC$, с основанием $AC$ и средней линией $MN$.
- Докажем, что $MNparallel AC$ и $MN=dfrac{1}{2}cdot AC$.
- На прямой $MN$ за точкой $N$ выберем точку $D$ так, чтобы
выполнялось $MN=ND$. - Тогда $ riangle BMN= riangle NDC$ по первому признаку
равенства ($BN=NC, MN=ND$, $angle BNM=angle DNC$). - Тогда $angle 1=angle 2$, следовательно, $ABparallel DC$.
- Кроме того, из равенства треугольников следует, что $MB=DC$.
- Но $MB=MA$, следовательно $MA=DC$.
- Тогда $AMDC$ – параллелограмм ($DC=MA$, $MAparallel DC$).
- Следовательно, $MDparallel AC$ и $AC=MD=2cdot MN$.
-
Если в треугольнике $ABC$ точка $M$ – середина стороны $AB$, а точка $N$ принадлежит стороне $BC$, и при этом $MNparallel AC$, то $MN$ – средняя линия.
-
Если в треугольнике $ABC$ точки $M$ и $N$ принадлежат сторонам $AB$ и $BC$ соответственно, при этом $MNparallel AC$ и $2|MN|=|AC|$, то $MN$ – средняя линия.
- Рассмотрим $ riangle ABC$, в котором $M$ – середина $AB$, $N$ лежит на стороне $BC$, $MNparallel AC$.
- Докажем, что $MN$ – средняя линия.
- Выберем на прямой $MN$ за точкой $N$ такую точку $D$, что $MD=AC$.
- Тогда $AMDC$ – параллелограмм ($AC=MD$, $ACparallel MD$).
- Следовательно, $angle B=angle 3, angle 1=angle 2$, так как $AMparallel CD$.
- Кроме того $AM=DC$, как противоположные стороны параллелограмма.
- Следовательно, $BM=MA=DC$.
- Тогда $ riangle BMN= riangle NDC$ по второму признаку равенства.
- Следовательно, $BN=NC$, то есть $MN$ – средняя линия.
Рассмотрим треугольник $ABC$, в котором на сторонах $AB$ и $BC$ взяты точки $M$ и $N$
соответственно так, что $MNparallel AC$ и $2cdot MN=AC$.
Докажем, что тогда $MN$ – средняя линия треугольника $ABC$.
Пусть $D$ – это середина $AC$. Тогда $MNCD$ – параллелограмм ($MN=DC$, $MNparallel DC$).
- Следовательно, $MDparallel NC$.
- Тогда $angle 1=angle C=angle 2$, как соответственные при
параллельных прямых. - Кроме того $angle A=angle 3$.
- Следовательно, $ riangle BMN= riangle AMD$ по второму признаку равенства.
- Тогда $BM=MA$ и $BN=MD=NC$, то есть $MN$ – средняя линия $ riangle ABC$.
Третий признак средней линии неверен.
math-public/srednyaya_liniya_treugolnika.txt · Последние изменения: 2016/04/13 19:46 — labreslav
Источник: http://wiki.sch239.net/math-public/srednyaya_liniya_treugolnika
Средняя линия треугольника
| Предмет, класс | Геометрия, 8 класс ( базовый учебник — Атанасян Л.С., Бутузов В.Ф.и др.- 20-е изд., Геометрия 7-9 классы,- М.: Просвещение, 2013) | ||
| Учитель | Марущенко Надежда Викторовна | ||
| Тема урока, № урока по теме | Средняя линия треугольника, урок №1. | ||
| Методическая цель | Формирование у учащихся способностей к структурированию и систематизации изучаемого предметного содержания и способностей к учебной деятельности. | ||
| Образовательная цель |
|
||
| Воспитательная цель | — Повышение коммуникативной активности учащихся, их эмоциональной включенности в учебный процесс, создание благоприятных условий для проявления индивидуальности, выбора своей позиции, формирование умения аргументировано и спокойно отстаивать свою точку зрения. — Воспитывать дисциплинированность, внимательность, культуру речи и письма. | ||
| Развивающая цель | — Способствовать развитию интереса к предмету, познавательной активности, самоконтроля, навыков исследовательской деятельности, а так же навыков работы с компьютерной техникой и интерактивной доской. — Стимулирование творчества обучающихся, развитие их способности к анализу информации, формирование умений сравнивать, анализировать, обобщать, развитие умений правильно и кратко выражать свои мысли. | ||
| Тип урока | Урок открытия новых знаний | ||
| Формы работы | Фронтальная, индивидуальная, парная. | ||
| Необходимое техническое оборудование | Компьютер,проектор, презентация подготовленная учителем. | ||
| Планируемый результат | Планируемые предметные результаты в предметном направлении и личностном развитии: Знание:
Умение: проводить исследования несложных ситуаций (сравнение средней линии и основания треугольника), формулировать гипотезы исследования, понимать необходимость ее проверки, доказательства, совместно работать в группе.
|
||
| Метапредметные результаты |
|
||
| Личностные УУД: Учатся умению вести диалог на основе равноправных отношений и взаимного уважения, формируют внутреннюю позицию на уровне положительного отношения к образовательному процессу, оценивают себя в социальных ролях: ученик, докладчик. | Познавательные УУД: | Коммуникативные УУД: | Регулятивные УУД: |
| Развивают навыки познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, овладевают навыками решения проблем, осознанно и произвольно строят речевые высказывания в устной и письменной форме. | Проявляют уважительное отношение к одноклассникам, внимание к личности другого, адекватное межличностное восприятие. Вступают в диалог, участвуют в коллективном обсуждении проблем, учатся владеть монологической и диалогической формами речи. | Выделяют и осознают то, что уже освоено и что еще подлежит усвоению, осознают качество и уровень усвоения. В диалоге с учителем учатся вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех. |
- СТРУКТУРА УРОКА.
- 1.
- 2.
- 3.
- 4.
- 6.
- 7.
Организационный этап. Мотивация.
— Здравствуйте ребята! Давайте начнем наш сегодняшний урок с доброжелательности. Повернемся к друг другу, улыбнемся. И с хорошим настроением отправимся в очередной путь по дороге к знаниям.
— А сопутствующими словами нам сегодня будут слова древнего мыслителя Конфуция:
Три пути ведут к знанию:Путь размышления – это путь самый благородный,Путь подражания – это путь самый легкий,И путь опыта – это путь самый горький.
— Сегодня мы продолжим знакомство с самой популярной в школьном курсе геометрической фигурой. Это самая простая замкнутая прямолинейная фигура, свойства которой человек узнал еще в глубокой древности, так как она имела широкое применение в практической жизни. Вы догадались, что это за фигура?
Актуализация опорных знаний.
— По каким признакам треугольники бывают подобными?- Как связаны соответствующие стороны и углы подобных треугольников?- Что такое коэффициент подобия, чему он равен?- Какие прямые называются параллельными?
- — Назовите признаки параллельности прямых
- Выполнение заданий на экране.
«Открытие» нового знания. Создание проблемной ситуации.
- а) построить в тетради треугольник: первому варианту – тупоугольный; второму варианту – прямоугольный; третьему варианту – остроугольный;б) ввести обозначение этого треугольника;в) отметить середины двух любых его сторон и обозначить их;
- г) соединить полученные точки отрезками.
- Учитель объясняет ученикам, что полученный ими отрезок называют средней линией треугольника и задает вопросы :
- – Почему она так названа?
- — Используя принцип построения, попробуйте сформулировать определение средней линии.
- – Сколько средних линий можно построить в треугольнике?
— Ребята, сейчас поработаем в парах: на каждой парте лежит заготовка треугольника. Отметьте середины двух любых его сторон и проведите среднюю линию. Давайте посмотрим на расположение средней линии треугольника относительно третьей стороны.
— Какие результаты вы получили? Какой вывод можно сделать?
- А теперь измерьте среднюю линию треугольника и его основание и найдите их отношение.
- — А теперь попробуйте сами сформулировать свойство средней линии треугольника.
- — Откройте учебники на странице 141 и давайте проверим к правильному ли выводу мы пришли.
- А теперь оформим в тетради данное утверждение в виде теоремы .
- — Вы, наверное, уже привыкли, что геометрия — это наука, в которой необходимо все обосновывать и доказывать.
— Мы сейчас докажем теорему. Разобраться в логике доказательства вам помогут печатные заготовки, которые есть у каждого из вас, возьмите их.
— Итак, что нам дано? Что необходимо доказать?
- — Доказываем (опираясь на доску и печатные заготовки).
- — Давайте еще раз пройдемся по доказательству.
- Первичное усвоение нового знания.
- — Вот ребята мы прошли с вами по пути размышления и пора перейти к пути опыта.
- — Посмотрите на экран и давайте выполним задания по готовым чертежам.
- Первичное закрепление.
- Решение задачи №566
- Информация о домашнем задании.
- Формулировка теоремы, доказательство по опорному конспекту. ТПО №
- Рефлексия
- Подведем итоги сегодняшнего урока.
- — Полностью ли реализован составленный нами план?
- – Соответствовала ли наша работа целям урока?
- — Что вы ожидали от сегодняшнего урока?
- — Что вызвало трудности?
- — Были ли задания, которые ты делал с удовольствием?
- — Какие знания, полученные ранее, нужны были для изучения новой темы?
- — А как вы считаете, знания, полученные сегодня на уроке, будут вам необходимы на следующих уроках.
- — Как вы оцените свою работу сегодня на уроке?
- А теперь я оценю вашу работу на уроке.
- Ребята приветствуют друг друга.
- — Треугольник.
- Называют ответы.
- Выполняют задания на экране.
Строят в тетрадях треугольники и поводят средние линии. Отвечают на вопросы.
- Свойства.
- Отличительная особенность.
- Отвечают на вопросы.
- Формулируют свойство
- Заполняют заготовки под руководством учителя.
- Работа по готовым чертежам
- Решение задачи у доски и в тетради
- Записывают домашнее задание в дневники.
- Отвечают на вопросы
- — сформировать доброжелательный рабочий настрой, проверить готовность класса к уроку
- На этом этапе урока учителю необходимо сформировать осознание предела имеющихся знаний (моих знаний не хватает, чтобы ответить на вопрос).
- — актуализировать опорные знания о равнобедренном треугольнике, высотах, медианах и биссектрисах треугольника;
- — формировать осознание предела имеющихся знаний и потребность в изучении нового материала;
- — развивать умения анализировать информацию;
- — умение выстраивать освоение учебного материала как совместную деятельность;
- — умение общаться с учащимися и вести диалог.
- Необходимо целенаправленно организовать слушание, предлагая специальные задания.
Выслушиваются все варианты ответов учащихся. Важно выделить учеников, давших правильный ответ, поддержать того, кто не смог дать верный ответ.
- Учителю желательно проявить свои чувства (радость, удивление) по поводу того, что дети сумели найти ответы на предложенные вопросы.
- — закрепить свойство средней линии треугольника в ходе решения задач.
- — организовать целостное осмысление и обобщение полученной информации, проведение оценки и самооценки учениками работы на уроке.
- — обеспечить понимание цели,
- содержания и способов выполнения домашнего задания.
Источник: https://infourok.ru/srednyaya-liniya-treugolnika-312555.html
Средняя линия треугольника — это… Что такое Средняя линия треугольника?
- Средняя линия — фигур в планиметрии отрезок, соединяющий середины двух сторон этой фигуры. Понятие употребляется для следующих фигур: треугольник, четырехугольник, трапеция. Содержание 1 Средняя линия треугольника 1.1 Свойства … Википедия
- СРЕДНЯЯ ЛИНИЯ — (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… … Большая политехническая энциклопедия
- СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции) отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Большой Энциклопедический словарь
- средняя линия — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции). * * * СРЕДНЯЯ ЛИНИЯ СРЕДНЯЯ ЛИНИЯ треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Энциклопедический словарь
- СРЕДНЯЯ ЛИНИЯ — треугольника отрезок, соединяющий середины двух сторон треугольника. Третья сторона треугольника при этом наз. основанием треугольника. С. л. треугольника параллельна основанию и равна половине его длины. Во всяком треугольнике С. л. отсекает от… … Математическая энциклопедия
- СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Естествознание. Энциклопедический словарь
- Средняя линия — 1) С. л. треугольника, отрезок, соединяющий середины двух сторон треугольника (третью сторону называют основанием). С. л. треугольника параллельна основанию и равна его половине; площади частей треугольника, на которые делит его с. л.,… … Большая советская энциклопедия
- Площадь треугольника — Стандартные обозначения Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника … Википедия
- Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
- Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Источник: https://dic.academic.ru/dic.nsf/ruwiki/500112




