Задача 1. В цилиндре ДВС адиабатно сжимается воздух с начальными параметрами p1 = 0.1 МПа и T1 = 300 К. Степень сжатия воздуха e = 10. К сжатому воздуху в изохорном процессе подводится теплота q = 288 кДж/кг. Определить параметры воздуха в узловых точках и рассчитать работу сжатия.

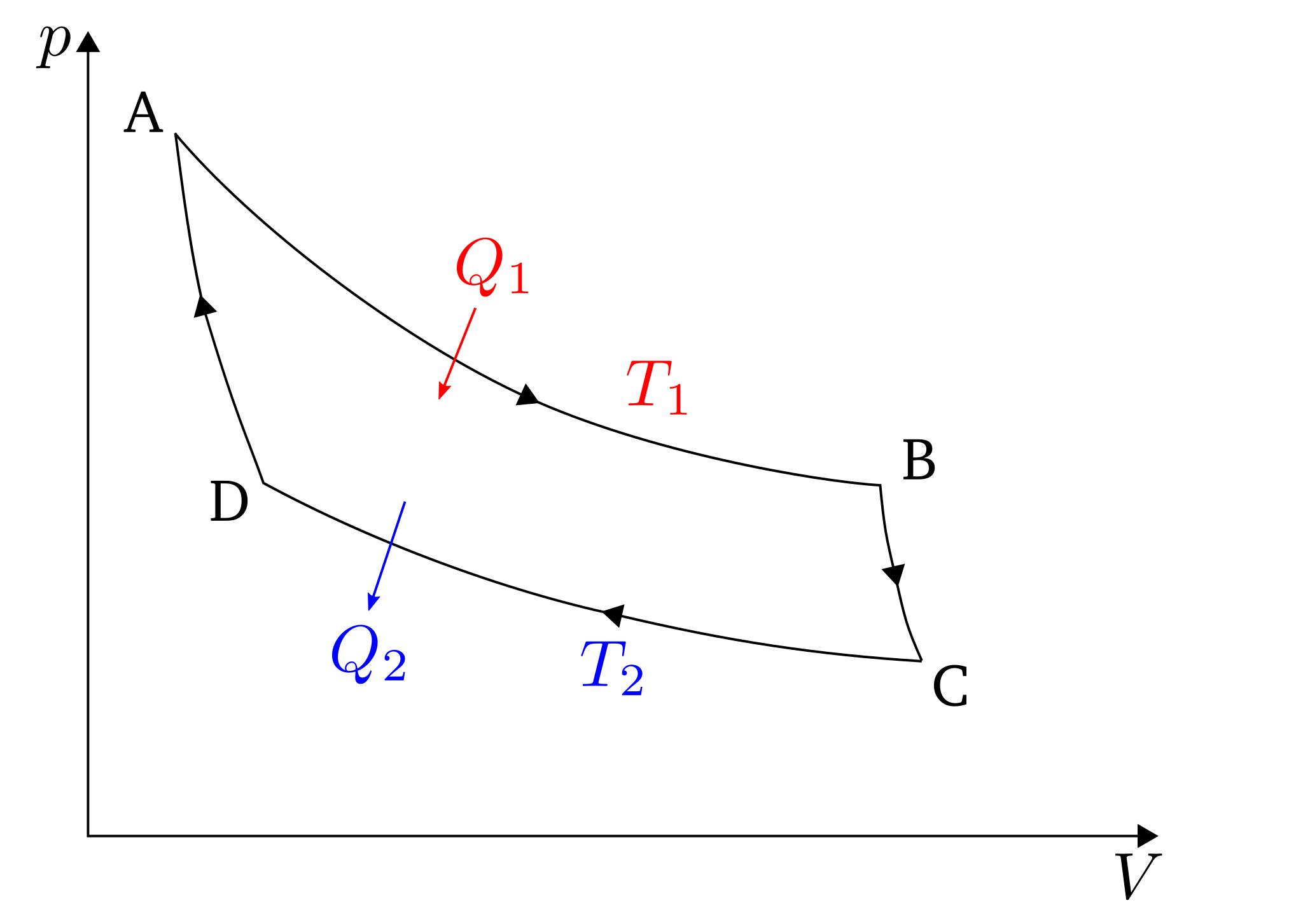
Изображаем адиабатный и изохорный процессы в диаграммах р-u и T-S. Процесс 1-2 адиабатного сжатия воздуха от V1 до V2 = V1/10 и процесс 2-3 изохорного подвода тепла. Из уравнения состояния определяем значение удельного объема в точке 1:
- p1u1 = RT1
- Откуда:
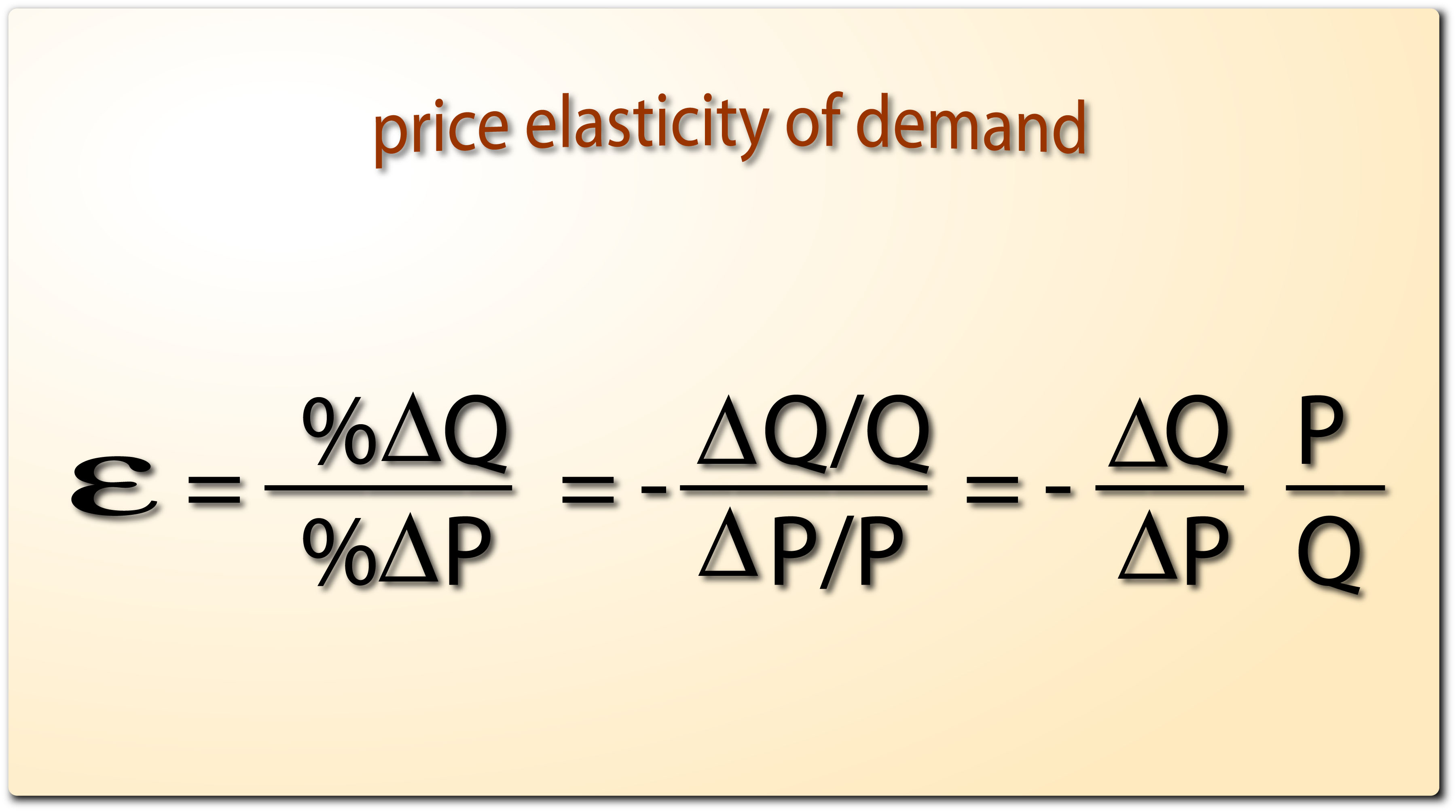
- Из уравнения соотношений удельных объемов и температур для адиабатного процесса определяем значение температуры в точке 2:

- Откуда:

- Определяем работу сжатия:
- Определяем параметры воздуха в узловых точках. Давление в точке 2 вычитается из уравнения соотношения удельных объемов и давлений для адиабатного процесса:
- Откуда:
- Тепло подведенное в изохорном процессе:
- q = cu(T3 – T2)
- Отсюда температура в точке 3:

- Из соотношений давлений и температур для изохорного процесса находим давление в точке 3:

Задача 2. Начальные параметры воздуха, адиабатно сжимаемого в компрессоре ГТУ.
р1=0,1 Мпа и Т1=29 К.. Степень повышения давления в компрессоре β = 5. Затем воздух подается в камеру сгорания, где при постоянном давлении к нему подводится теплота в количестве 242 кДж/кг. Определить параметры воздуха в узловых точках и работу сжатия компрессора.

Изобразим адиабатный и изобарный процессы в диаграммах p-u и T-S. Процесс 1-2 повышения давления воздуха от p1 = 0,1 МПа до p2 = 0,5 МПа, и процесс 2-3 изобарного (при p2 = const) подвода тепла.
- Определяем из уравнения состояния значение удельного объема в точке 1:

- Из уравнения соотношения давлений и температур для адиабатного процесса определяем значение температуры в точке 2:
- Определяем работу сжатия :
- Удельный объем в точке 2 находим из уравнения состояния:
- p2 x v2 = RT2
- Откуда:
- Процесс 2-3 изобарный, поэтому:
- P2 = P3 = 0,5 МПа
- В процессе 2-3 подведено тепло:
- q = Cp (T3 — T2)
- Отсюда:
- Удельный объем в точке 3:
Задача 3. Воздух, начальные параметры которого р1=0,1 МПа и Т1=300 К адиабатно сжимается в компрессоре турбонагнетателя ДВС до давления p2 = 0,28 МПа, затем при р=const воздух охлаждается в холодильнике до температуры t3=37С°. Определить работу сжатия компрессора и количество теплоты отводимой от 1 кг воздуха.
- Из уравнений адиабатного процесса определяем температуру Т2 в конце процесса сжатия компрессора.
- Откуда:
- Количество отводимой теплоты:
- Работа сжатия компрессора:
Источник: https://tehnar.net.ua/adiabatnyiy-protsess-primeryi-resheniya-zadach/
Теория горения и взрыва
Качественное отличие взрывного горения от дефлаграционного связано с особо благоприятными условиями для взаимодействия горючего и окислителя. При взрывном горении выделение теплоты происходит настолько быстро, что формируется ударная (взрывная) волна, движущаяся по объёму горящей смеси.
Процессы взрывного горения всегда связаны с протеканием цепных реакций. Такие химические реакции обычно ускоряются не за счет разветвления цепей, а за счет саморазогрева газовой смеси, что в дальнейшем может приводить к возникновению теплового взрыва.
Определяющую роль при взрывном горении играют источник инициирования реакции, теплопроводность вещества и диффузия активных центров, вызывающих протекание цепной реакции.
Механизм протекания цепной реакции, описанный академиком Н.Н. Семеновым, присущ многим реальным процессам. В 1924 году его ученик Ю.Б. Харитон фактически дал старт новому научному направлению, экспериментально показав существование разветвленных цепных химических реакций.
Измеряя интенсивность свечения фосфора при его окислении, он заметил, что даже при самых малых изменениях условий проведения опыта (концентрации реагентов, температуры, примесей и даже размера сосуда) реакция ускорялась скачкообразно.
Механизм цепных реакций в 1926 году описал его научный руководитель Н.Н. Семенов, через тридцать лет получивший за эти исследования Нобелевскую премию по химии. На основе работ Н.Н. Семенова были разработаны в дальнейшем теории цепного и теплового взрыва.
Они явились химическими аналогами того, что происходит в атомной и водородной бомбах.
Предложенная Н.Н. Семеновым теория сразу вошла в моду, так как дала объяснение причине чудовищного и загадочного взрыва, произошедшего в 1921 году на одном из немецких складов: на воздух взлетело сразу несколько тысяч тонн аммиачной селитры.
При этом для разрушения массива слежавшейся селитры применяли небольшие взрывы. Харитон Ю.Б. подсчитал, что в огромной массе материала, до того казавшегося инертным, время разлета сжатого вещества превысило время реакции.
В дальнейшем такой подход (принцип Харитона) пригодился и при создании сверхмощных отечественных авиабомб и боезарядов для артиллерии, включая системы «Катюши».
При анализе взрывных явлений многие ученые отмечали, что причинами ускорения скорости распространения пламени (интенсификации горения) могут быть различные газодинамические и теплофизические явления, например, подогрев смеси газов и воздуха, повышение давления и др. При таких определенных условиях взрывное горение далее может перейти в детонационное.
В процессах взрыва газовоздушных смесей развиваются ударные волны, на фронте которых достигаются высокие параметры: скорость распространения пламени, давление и температура.
Иногда они могут инициировать возникновение детонации. Реальная вероятность возникновения детонационного горения взрывоопасных сред на производстве весьма мала, т. к.
в большинстве случаев критических параметров достичь не удается.
Взрывное горение сопровождается ударной волной, которая представляет собой распространяющуюся волну скачка уплотнения газа.
Она создается при эффективной видимой скорости пламени, равной примерно 0,2. Здесь — число Маха, определяемое отношением фактической скорости перемещения газа к скорости звука в данной среде.
Для углеводородовоздушных смесей это соответствует видимой скорости движения пламени около 60 м/с.
Наиболее широкое применение взрывные явления нашли в военном деле, где для этого используются различные конденсированные взрывчатые вещества.
Эти вещества (неядерные) относятся к химическим взрывчатым веществам, так как энергия при их взрыве выделяется за счет протекания химических реакций горючего и окислителя, которые содержатся во взрывчатом веществе.
Большая часть используемых на практике взрывчатых веществ – твердые вещества. Вместе с тем широко применяются и могут образоваться в промышленности газообразные взрывоопасные смеси.
Источник: http://ido.tsuab.ru/mod/book/view.php?id=10764&chapterid=3106
ПОИСК
Принципиальная схема детандерного расширения представлена на рис. 41. Детандерное расширение характеризуется постоянством энтропии процесса. Газ засасывается компрессором К при давлении pi и температуре Ti и изотермически сжимается до давления р2 (линия 1—2).
Сжатый газ расширяется в детандере Д-Р до первоначального давления рь Теоретически расширение в детандере происходит при постоянной энтропии (линия 2—3) и газ должен охладиться при этом до температуры Тг. При этом работа, совершаемая 1 кг газа в детандере, равна /i2—h-л.
В действительности процесс в детандере отклоняется от адиабатического и расширение происходит по политропе (линия 2—< ).
Энтальпия газа после расширения будет при этом h i, и работа, затрачиваемая в детандере, составит /дет = /1г— з-Отношение действительной работы к теоретической называется коэффициентом полезного действия детандера [c.
124] При адиабатическом сжатии газа тепло извне не подводится и не отводится, поэтому вся работа, затрачиваемая на сжатие газа, идет на увеличение его энтальпии, т. е. температуры. Работа, затрачиваемая на адиабатическое сжатие газа, равна [c.107]
Затрата энергии на сжатие газа в адиабатическом процессе будет больше, чем в изотермическом. При политропическом процессе затрата работы на сжатие газа составит [c.107]
Охлаждение газов при их расширении в детандере. В данном случае расширение предварительно сжатого газа происходит в газовом двигателе, который одновременно совершает внешнюю работу последняя может быть использована для любых целей, например для перекачки жидкостей или нагнетания газов.
Расширение сжатого газа в детандере происходит без обмена теплом с окружающей средой, и совершаемая при этом газом работа производится за счет его внутренней энергии, в результате чего газ охлаждается.
Предельная температура охлаждения определяется по общему уравнению (IV, 1) для адиабатического расширения идеального газа. [c.652]
Соответственно для адиабатического процесса сжатия газа уравнение (7-29) выразится следующим образом [c.218]
Задача 111.23. Метан при 20° С подвергается многоступенчатому сжатию от 1,5 до 90 ат с промежуточным охлаждением до начальной температуры. Определить увеличение потребляемой мощности при нарушении работы промежуточных холодильников и охлаждении газа только до 40° С, Сжатие считать адиабатическим (показатель адиабаты A=l,31). [c.95]
Газ засасывается компрессором К при давлении р, и температуре Г, и изотермически сжимается до давления р2- Сжатый газ расширяется в детандере до первоначального давления р,.
Теоретически расширение в детандере происходит при постоянной энтропии, и газ должен охладиться при этом до температуры Гз- В действительности процесс в детандере несколько отклоняется от адиабатического.
[c.128]
Поскольку теплопроводность разреженного газа очень мала и теплообмен со стенками цилиндра практически отсутствует, сжатие газа в сухих вакуум-насосах происходит адиабатически. Как следует из уравнения (IV,8), удельная работа адиабатического сжатия 4д — = О при Р2/Р1 = 1, т. е. в начальный момент, когда = 1 ат, и при достижении [c.173]
Процесс адиабатического сжатия газа характеризуется полным отсутствием теплообмена между газом и окружающей средой. При адиабатическом сжатии газа dQ = О и из уравнения (IV,2) следует, что dS = 0. [c.154]
В компрессорах, работающих без охлаждения газа, происходит дополни гельный нагрев его в результате отсутствия отвода тепла, выделяемого при трении быстро движущихся деталей машины о газ, вследствие гидравлических сопротивлений и других причин.
Сжатие газа в таких машинах протекает по политропе, показатель которой пг Н> к. Поэтому мощность сжатия в неохлаждаемых компрессорах принято сравнивать с мощностью сжатия в условной машине, сжимающей газ по адиабате (изоэнтропно).
Эта машина называется изоэнтропной и является наиболее экономичной машиной из класса компрессоров, работающих без охлаждения газа. Отношение мощности сжатия изоэнтропной машины Л т.
ад к мощности N данного компрессора, работающего без охлаждения газа, называется изоэнтропным (адиабатическим) к. п. д.т)ад [c.156]
Теоретически процесс сжатия газа в компрессоре может быть адиабатическим или изотермическим. [c.217]
Как известно, площадь диаграммы выражает работу, совершаемую в процессе сжатия газа. Легко видеть, что эта работа будет наименьшей при изотермическом сжатии и наибольшей — при адиабатическом. При охлаждении газа в компрессоре через рубашку процесс сжатия приближается к изотермическому, причем соответственно снижается расход энергии на сжатие газа. [c.224]
Истинная мольная теплоемкость газообразных углеводородов с повышением температуры и молекулярного веса возрастает.
При одном и том Hie числе углеродных атомов в молекуле наибольшая теплоемкость соответствует углеводородам парафинового ряда. Отпо-Hienne pj v к является показателем адиабаты.
Им пользуются при вычислении истинной мольной теплоемкости при постоянном объеме, а также в расчетах адиабатического сжатия газов по формуле [c.64]
Адиабатическое расширение сжатого газа с производством внешней работы. Этот метод также используется для получения глубокого холода. В данном случае адиабатическое расширение рабочего газа производят в специальной расширительной машине — детандере.
Детандер — это поршневой (при методе Клода) или центробежный (при методе Капицы) двигатель, работающий за счет расширения сжатого рабочего газа. Мощность, развиваемая детандером, обычно используется для частичного покрытия потребности в энергии самой холодильной установки.
[c.475]
Идеальный цикл сжижения газа. Определим, пользуясь Т — «-диаграммой (рис. XVI1-2), минимальную затрату работы при идеальном обратимом процессе сжижения газа.
Начальное состояние газа характеризуется точкой / (Г), г,), а его состояние после сжижения — точкой 3.
1 1деяльпый процесс осуществляется путем изотермического сжатия газа (линия /—2) и его адиабатического, или нзоэнтропического, расширения (линия 2—3). [c.649]
Отношение изобарной теплоемкости к изохорно Ср1Су называется показателем адиабаты и используется пзи расчетах адиабатического сжатия газа (рис. 6). Чаш,е всего приходится иметь дело с политропическим сжатием или расширением. Для инженерных расчетов показатель политропы берется равным /г = 0,95 Ср/Су. [c.46]
При возбуждении ударной волны в химически реагирующем горючем газе под влиянием адиабатического сжатия смеси наряду с ударной волной возникает волна горения. Совокупность этих волн представляет собой детонационную волну.
В детонационной волне потери на трение и теплоотдачу при ее движении по трубе компенсируются энергией, выделяющейся в волне горения. Благодаря этому при распространении по трубе детонационной волны становится возможным стационарный режим, когда скорость детонации (О) остается постоянной.
Условие существования стационарного режима определяется правилом Чемпена — Жуге, согласно которому стабильность детонационной волны достигается, если скорость потока сжатого газа за фронтом детонационной волны равна или выше скорости звука в этом газе.
Правило Чемпена — Жуге позволяет найти на адиабате Гюгоньо точку с такими значениями Рг и Уг, которые обеспечивают стабильность детонационной волны и позволяют вычислить скорость детонации В [c.141]
Принимая сжатие газа в каждой ступени адиабатическим, по уравнению (40) получим [c.130]
Адиабатическое воспламенение возможно, например, при работе компрессоров. Поэтому очень важен отвод тепла, образующегося при сжатии газов. Адиабатическое воспламенение — одна из причин возникновения наиболее опасного детонационного горения. [c.204]
В газообразных системах причиной местного адиабатического сжатия газа может служить ударная волна, возникающая при резком открывании вентилей и прО [c.28]
Минимальная затрата работы будет при идеальном процессе сжижения газа, который можно представить осуществляемым путем изотермического сжатия и адиабатического расширения. Как видно из Т—5-диаграммы (рис. 482), в таком процессе газ сжимается изотермически при температуре Тх от точки А до точки В по прямой АВ.
После сжатия газ адиабатически расширяется по вертикали ВС, превращаясь в жидкость. Газ подвергается также охлаждению, причем при помощи охлаждающей воды от него отнимают не только тепло в количестве, необходимом для сжижения, но и тепло, выделившееся в результате изотермического сжатия [c.
706]
Линии сжатия и расширения — политропы с переменным показателем, что наглядно показано на диаграмме 5, Т (рис. 18.1, б). В начале сжатия (точка а) температура газа ниже температуры стенок цилиндра и поршня. Поэтому процесс сжатия происходит с подводом тепла при показателе политропы большем, чем показатель адиабаты.
При сжатии температура газа повышается, и направление теплообмена изменяется, как только температура газа превышает температуру стенок цилиндра и поршня. Газ начинает отдавать тепло, а показатель политропы изменяется от п > /г в начале сжатия до и < /г в конце сжатия.
При равенстве температур газа и окружающих стенок на мгновение теплообмен прекращается, и сжатие становится адиабатическим (п = к). [c.231]
Допустим, что состоя51ие сжатого газа перед детандером характеризуется температурой Т, = 205 К и давлением = 100 ат — точка 1. Процесс адиабатического расширения газа с отдачей пненшей работы осушествляется при S = onst.
Поэтому опустив из точки 1 вертикаль вниз до пересечения с изобарой, отвечающей заданному конечному давлению Рз = сип, найдем точку 4, характеризующую состояние газа в конце детандирования.
Этой точке соответствует температура Т4 = 82 К и, следовательно, понижение температуры газа ЛГ [c.653]
Первый член правой части этого уравнения будет иметь различные значения в зависимости от характера теплообмена с окружающей средой. Весьма характерным является адиабатический к. п. д., при котором в качестве эталона для сравнения принимается работа сжатия газа в идеальных условиях отсутствия теплообмена и потерь, [c.34]
Газ сжимается изотермически по линии / — 5 до необходимого давления Рз, и выделяющаяся при сжатии теплота отводится охлаждающей водой в холодильнике. Сжатый газ адиабатически расширяется по линии 3 — Ос совершением внешней работы, его температура понижается и в конце расширения (точка 0) це.ликом сжижается. [c.83]
Характерные особенности имеет так называемое адиабатическое воспламенение в результате адиабатического сжатия газов.
Если нагреть горючую смесь, находящуюся в сосуде с холодными стенками, путем адиабатического сжатия, т. е. достаточно быстро, то она может воспламениться.
Это произойдет в том случае, если вследствие начавшейся реакции тепла выделяется больше, чем отводится. [c.204]
Для третьей стадии цикла работа будет отрицательна, так как происходит сжатие газа и д = —nRT n VJV ,), где по условию Кд = ЗКь а объем должен быть получен согласно указанию о том, что после адиабатического сжатия газ должен вернуться в исходное состояние, следовательно, должно быть равенство [c.69]
Энергетическое разделение сжатого газа на охлажденный и нагретый потоки в адиабатических условиях осуществляют в вихревой трубе (ВТ) (1) при [c.9]
Процесс сжатия газа в турбокомпрессорах аналогичен сжатию газа в турбогазодувках. Как видно из рис.
IV-15, после сжатия в группе неохлаждаемых колес турбокомпрессора (линии АС, DE и FG) газ имеет температуру более высокую, чем температура в конце адиабатического сжатия (точки В).
Так же как и в турбогазодувках, увеличение температуры газа сверх адиабатической происходит вследствие дополнительного нагрева газа за счет тепла, выделяемого при трении его о лопатки и плоскости вращающихся рабочих колес. [c.170]
Сравнение выражений для ад. И /из. показывает, что при изотермическом сжатии газа расход энергии меньше, чем при адиабатическом процессе.
Поэтому стараются по возможности осуществлять процесс сжатия газа изотермически, для чего приходится отнимать от сжимаемого газа определенное количество тепла.
С этой целью цилиндры компрессоров снабжают либо наружными ребрами для воздушного охлаждения, либо специальными рубашками для водяного охлаждения. Однако [c.175]
Для процесса адиабатического сжатия в идеально изолированном цилиндре, учитывая, что dQ = 0, дифференциал работы процесса адиабатического сжатия газа в соответствии с зависимостями (111-120) и (111-22) равен [c.248]
Процессы сжатия газа в компрессоре изображаются на диаграмме Т—5 следующим образом. При адиабатическом сжатии q = 0, следовательно по формуле (7-31) AS = 0, т. е.
процесс идет без изменения энтропии (S = onst). Поэтому.
процесс изображается вертикальной линией 1—2, причем точка 1 характеризует состояние газа до сжатия и лежит на пересечении изобары р и изотермы Т] точка 2 отвечает [c.219]
Отличительной особенностью многоступенчатого теоретического цикла (рис. 23) от одноступенчатого является ступенчатое сжатие газа адиабатическое или политропическое сжатие в цилиндрах чередуется с изобарическим сжатием в промежуточных холодильниках. Процесс многоступенчатого сжатия в V, Р- и s, Г-диаграм-мах представлен на рис. 23. [c.58]
Дросселирование сжатого газа. Дросселирование, т. е. пропускание газа через узкую щель, приводит к его адиабатическо-лу расширению без отдачи внешней работы. При этом в случае [c.474]
Если время адиабатического сжатия газа нри прохождении звуковой волны заметно превышает время колебательной релаксации Ткол то молекулярную колебательную теплоемкость можно считать близкой к равновесной колебательной теплоемкости С ол- В тех же случаях, когда полупериод колебаний меньше вс личины Ткол (большие частоты), колебательная теплоемкость будет практически равна нулю, т. е. вся заключенная в данном элементе газа энергия будет иметь форму поступательной и вращательной энергии. [c.77]
Процессы сжатия газа. При изменяющихся давлении и объеме в зависимости от характера теплообмена с окружающей средой изменение состояния газа может происходить изотермически, адиабатически и политропически. [c.106]
Практический интерес представляют а) адиабатическое, или изоэнтропическое, расширение предварительно сжатых газов в расширительной машине (детандере) и б) изоэнталъпическое их расширение при пропускании через дросселирующий вентиль. [c.206]
Источник: https://www.chem21.info/info/94679/
12. Адиабатический процесс. Уравнение Пуассона для адиабатического процесса. Показатель адиабаты
Адиабатический,
процесс — термодинамический
процесс в
макроскопической системе, при котором
система не обменивается теплотой с
окружающим пространством. Адиабатические
процессы обратимы только
тогда, когда в каждый момент времени
система остаётся равновесной (например,
изменение состояния происходит достаточно
медленно) и изменения энтропии не
происходит.
Обратимый
адиабатический процесс для идеального
газа описывается
уравнением
Пуассона.
Линия, изображающая адиабатный процесс
на термодинамической диаграмме,
называется адиабатой
Пуассона.
Примером необратимого адиабатического
процесса может быть распространение ударной
волны в
газе. Такой процесс описывается ударной
адиабатой.
где —
изменениевнутренней
энергии тела, —работа,
совершаемая системой.
Изменения энтропии S системы
в обратимом адиабатическом процессе
вследствие передачи тепла через границы
системы не происходит:
Здесь —
температура системы,—
теплота, полученная системой. Благодаря
этому адиабатический процесс может
быть составной частью обратимого цикла.
Адиабата
Пуассона
Для идеальных
газов,
чью теплоёмкость можно считать постоянной,
в случае квазистатического
процесса адиабата
имеет простейший вид и определяется
уравнением
где —
егообъём,
png» width=»64″>—показатель
адиабаты, и
png» width=»24″>—теплоёмкости газа
соответственно при постоянном давлении
и постоянном объёме.
График
адиабаты (жирная линия) на диаграмме
для газа.
—
давление газа;—
объём.
С
учётом уравнения
состояния идеального газа уравнение
адиабаты может быть преобразовано к
виду
Поскольку всегда
больше 1, из последнего уравнения следует,
что при адиабатическом сжатии (то есть
при уменьшении
png» width=»14″>)
газ нагревается (возрастает),
а при расширении — охлаждается, что
всегда верно и для реальных газов.
Нагревание при сжатии больше для того
газа, у которого больше коэффициент.
При
адиабатическом процессе показатель
адиабаты
равен .
Для
нерелятивистского невырожденного
одноатомного идеального газа ,
для двухатомного
png» width=»64″>,
для трёхатомного
png» width=»64″>,
для газов, состоящих из более сложных
молекул, показатель адиабатыопределяется
числомстепеней
свободы (i)
конкретной молекулы, исходя из
соотношения .
Для
реальных газов показатель адиабаты
отличается от показателя адиабаты для
идеальных газов, особенно для низких
температур, когда большую роль начинает
играть межмолекулярное
взаимодействие.
Один из методов для экспериментального
определения показателя был предложен
в 1819 г. Клеманом и Дезормом.
Стеклянный
баллон вместимостью несколько литров
наполняется исследуемым газом при
давлении Затем
открывается кран, газ адиабатически
расширяется, и давление падает до
атмосферного —
png» width=»20″>.
Затем происходит егоизохорное нагревание
до температуры окружающей среды. Давление
повышается до .
В результате такого эксперимента k можно
вычислить как
png» width=»89″>
Источник: https://studfile.net/preview/6154627/page:8/




