Формула силы лоренца

Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца.

Это явление является одним из основополагающих в электротехнике и электронике, на ряду с законом Кулона, электромагнитной индукцией Фарадея и прочими. Она воздействует на заряды, которые двигаются в магнитном поле.

В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.

Определение

Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.

• 
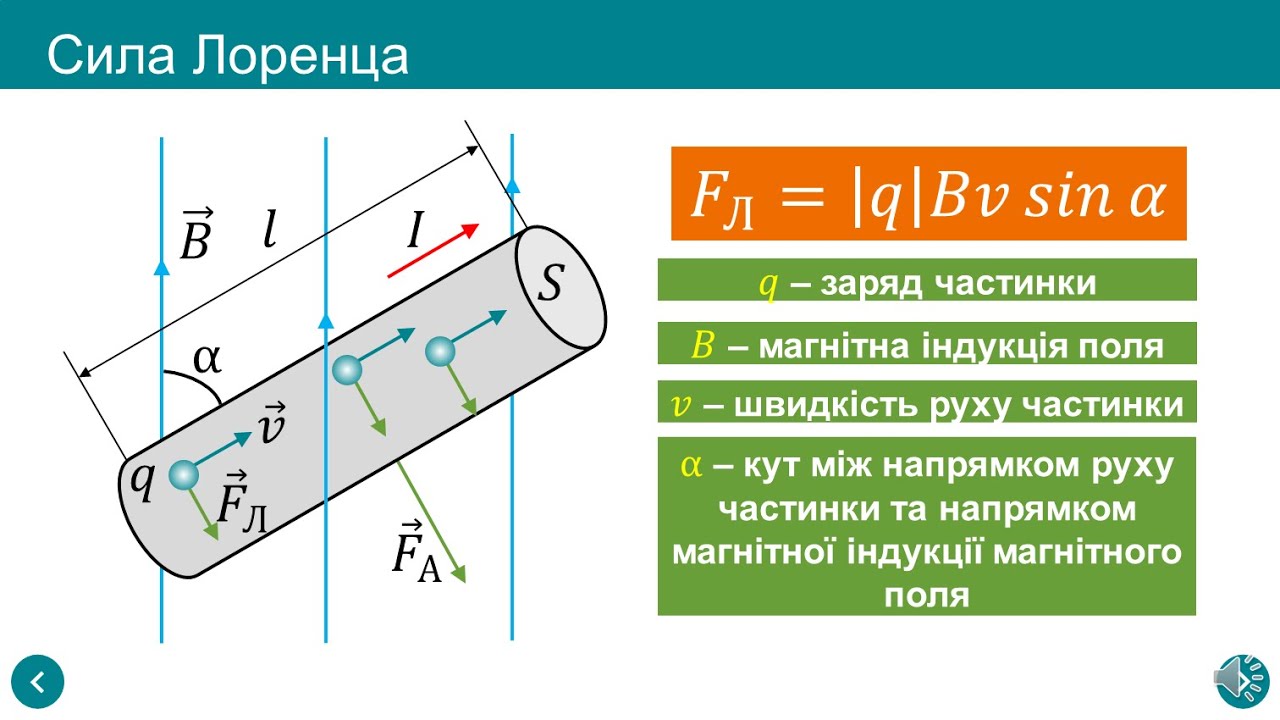
• Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:
• 
• Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:
• 

Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.

Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.

Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.

Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:

Как направлена сила Лоренца

Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки.

Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости.

Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды.

Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц.

Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.

Применение

Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.

Тем не менее, есть и другие случаи, где применяется это явление. Например:

• Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
• Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
• В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.

Заключение

Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:

1. Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
2. Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
3. Не влияет на скорость частицы.
4. Влияет на направление частицы.

Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.

Напоследок рекомендуем просмотреть полезные видео для закрепления изученного материала:

Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если возникли вопросы, задавайте их в х под статьей!

Материалы по теме:

Источник: https://samelectrik.ru/chto-takoe-sila-lorenca-kakovy-velichina-i-napravleniya-etoj-sily.html

Сила Лоренца: определение, направление, формула, применение

Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля.

Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так.

На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.

Определение и формула

Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.

Рис. 1. Выводы Лоренца

Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.

По закону Ампера:

Учитывая, что

(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:

Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:

Модуль F вычисляется по формуле:

Из формулы следует:

1. Сила Лоренца приобретает максимальное значение, если угол α прямой.
2. Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
3. Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).

Рис. 2. Заряженная частица между полюсами магнитов Рис. 3. Ориентация вектора в зависимости от полярности заряда

Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).

Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы.

Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле.

Эта составная направлена параллельно к электромагнитным линиям.

В чём измеряется?

Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0

Источник: https://www.asutpp.ru/sila-lorentsa.html

Сила Лоренца. Движение зарядов в магнитном поле

Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше.

Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие.

Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.

• Сила, действующая на проводник стоком (из закона Ампера), будет равна:
• 
• По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:
• Где: n0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:
• Подставив данное выражение в формулу Ампера, мы получим:
• 
• Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:
• Тогда выражение для силы Лоренца будет иметь вид:
• 
• Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:
• 

За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.

Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.

Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.

1. Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:
2. 
3. Где Е – напряженность электрического поля.
4. Рассмотрим небольшой пример:

Электрон, прошедший ускоряющую разность потенциалов 3,52∙103 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.

Решение:

Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.

В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца FЛ = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:

• Кинетическую энергию, которая будет равна mV2/2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим:
• Преобразовав эти соотношения и исключив из них скорость, получим формулу для определения удельного заряда электрона:
• Подставив исходные данные, выраженные в СИ, получим:
• 
• Проверяем размерность:
• 
• И кому интересно — видео о движении заряженных частиц:

Источник: https://elenergi.ru/sila-lorenca-dvizhenie-zaryadov-v-magnitnom-pole.html

Действие магнитного поля на движущийся заряд. Сила Лоренца — Класс!ная физика

«Физика — 11 класс»

Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током. Какова же сила, действующая на одну частицу?

1. Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества. Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля равна F = | I | BΔl sin α, а сила тока в проводнике равна I = qnvS где q — заряд частиц n — концентрация частиц (т.е. число зарядов в единице объема) v — скорость движения частиц S — поперечное сечение проводника. тогда получаем:

На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

• где α — угол между вектором скорости и вектором магнитной индукции.
• Сила Лоренца перпендикулярна векторам и .
• 2. Направление силы Лоренца
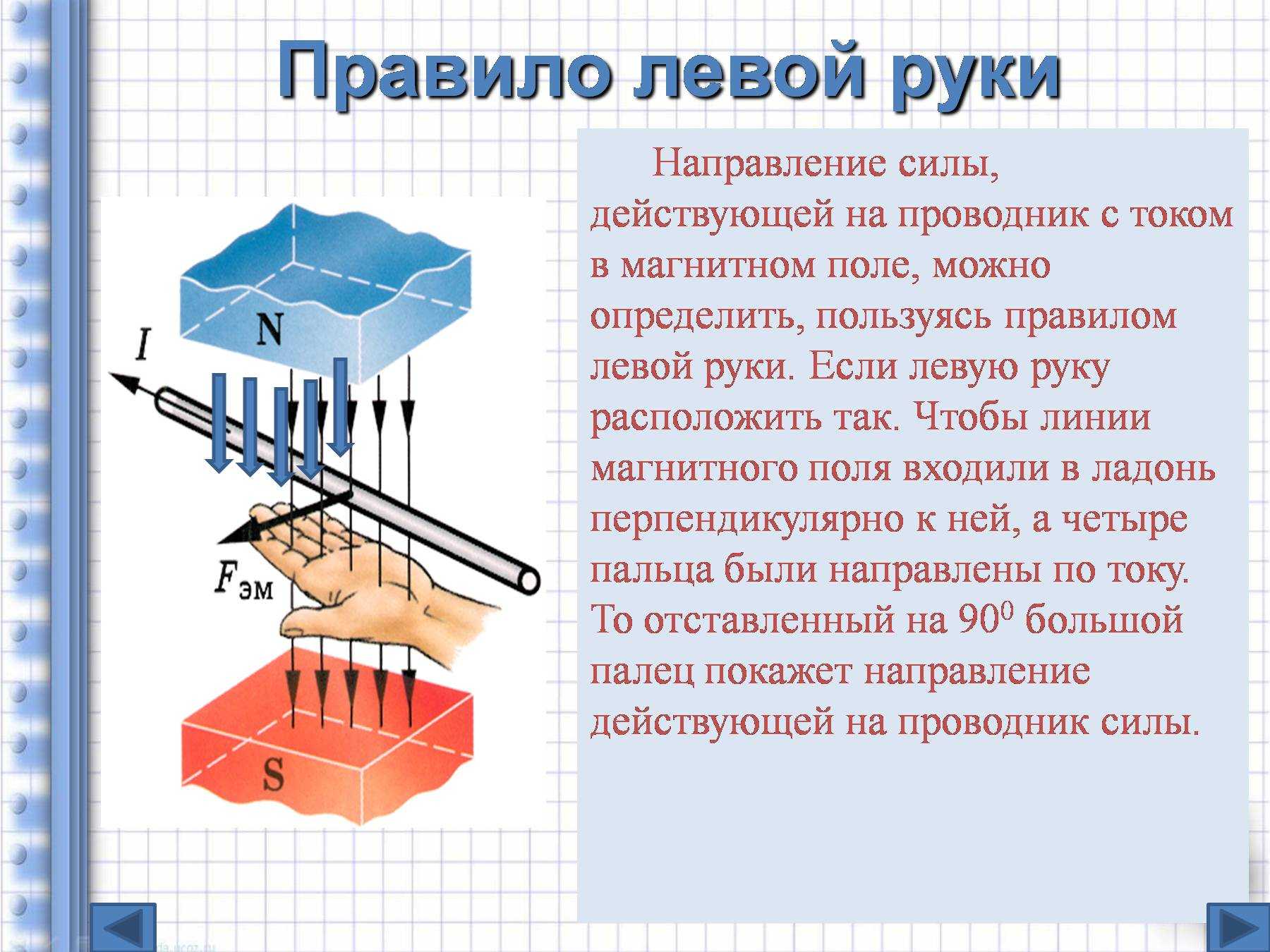
• Направление силы Лоренца определяется с помощью того же правила левой руки, что и направление силы Ампера:
• Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца Fл.

3. Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:

= эл + л где сила, с которой электрическое поле действует на заряд q, равна Fэл = q.

4. Cила Лоренца не совершает работы, т.к. она перпендикулярна вектору скорости частицы. Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.

1. Под действием силы Лоренца меняется лишь направление скорости частицы.
2. 5. Движение заряженной частицы в однородном магнитном поле

Есть однородное магнитное поле , направленное перпендикулярно к начальной скорости частицы .

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля. Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.

Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.

Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что

• В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.
• Согласно второму закону Ньютона

Тогда радиус окружности, по которой движется частица, равен:

Время, за которое частица делает полный оборот (период обращения), равно:

6. Использование действия магнитного поля на движущийся заряд.

Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.

На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Следующая страница «Магнитные свойства вещества» Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика

Магнитное поле и взаимодействие токов — Магнитная индукция. Линии магнитной индукции — Модуль вектора магнитной индукции. Сила Ампера — Электроизмерительные приборы. Громкоговоритель — Действие магнитного поля на движущийся заряд. Сила Лоренца — Магнитные свойства вещества — Примеры решения задач — Краткие итоги главы

Источник: http://class-fizika.ru/11_5.html

11 класс

• Физика
• Пройдите тест по явлению ЭМИ!
• Пройдите тест по природе света!

Электродинамика       

             Магнитное поле

                        Взаимодействие токов. Магнитное поле. Магнитная индукция. Вихревое поле

                        Сила Ампера. Электроизмерительные приборы. Громкоговоритель. Сила Лоренца

                        Электромагнитная индукция. Открытие ЭМИ. Магнитный поток

                        Самоиндукция. Индуктивность. Энергия магнитного поля

1.                         Магнитные свойства вещества
2.                          Уравнения Максвелла*
3.              Механические колебания
4.                         Свободные и вынужденные колебания. Условия возникновения колебаний
5.                         Динамика колебательного движения. Энергия колебательного движения

                        Сложение гармонических колебаний. Резонанс. Автоколебания

•              Электромагнитные колебания
•                         Свободные и вынужденные электромагнитные колебания. Колебательный контур
•                         Переменный электрический ток. Активное, ёмкостное, индуктивное сопротивление в цепи переменного тока
•                         Электрический резонанс. Мощность в цепи с активным сопротивлением

                        Генерирование электрической энергии. Трансформаторы. Производство, передача и использование электрической энергии

             Механические волны

                        Механические волны.  Длина волны. Скорость волны. Свойства волн

                        Звуковые волны. Звук. Эффект Допплера

             Электромагнитные волны

                        Электромагнитные волны. Экспериментальное обнаружение и свойства электромагнитных волн

                        Распространение радиоволн. Радиолокация. Телевидение. Развитие средств связи

1. Оптика           
2.              Геометрическая оптика
3.                         Развитие взглядов на природу света
4.                         Основные понятия геометрической оптики. Фотометрия

                        Принцип Гюйгенса и Ферма. Закон отражения. Закон преломления света. Полное отражение

•                          Плоское зеркало. Сферическое зеркало
•                                                                     Задачи на сферическое зеркало
•              Линза 
•                         Линза. Формула тонкой линзы
•                         Построение изображений, даваемой линзой
•                         Оптические приборы
•              Волновая оптика
•                         Скорость света
•                         Дисперсия света. Интерференция света
•                         Дифракция света. Дифракционная решётка
•                         Поляризация света
• Основы теории относительности  
•                         Законы электродинамики и принцип относительности
•                         Постулаты теории относительности. Релятивисткой закон сложения скоростей
•                         Зависимость массы тела от скорости его движения. Связь между массой и энергией
• Основы квантовой физики
•              Излучения и спектры
•                         Виды излучений. Источники света
•                         Спектры и спектральный анализ
•                         Инфракрасное, ультрафиолетовое и рентгеновское излучение
•                         Шкала электромагнитных излучений
•              Световые кванты
•                         Физические истоки квантовой теории
•                         Теория фотоэффекта. Применение фотоэффекта

                        Фотоны. Давление света. Гипотеза де Бройля

1.              Атомная физика
2.                         Опыт Резерфорда. Ядерная модель атома
3.                         Квантовые постулаты Бора. Модель атома водорода по Бору
4.                         Атом водорода в квантовой механике
5.                         Вынужденное излучение света. Лазеры
6.                         Открытие радиоактивности. Альфа-, Бета-, гамма- излучения
7.                          Методы наблюдения и регистрации радиоактивных излучений
8.                         Радиоактивные превращения

                        Закон радиоактивного распада. Период полураспада. Изотопы

             Ядерная физика

                        Открытие нейтрона. Состав ядра атома

                        Ядерные силы. Энергия связи атомных ядер. Ядерные спектры

                        Ядерные реакции. Энергетический выход ядерных реакций

                        Деление ядер урана. Цепные ядерные реакции. Ядерный реактор

•                         Термоядерные реакции. Применение ядерной энергии
•                         Получение радиоактивных изотопов и их применение. Биологическое действие радиоактивных излучений
•              Физика элементарных частиц
•                         Стандартная модель элементарных частиц
•                         Открытие позитрона. Античастицы
•              Современная физическая картина мира
•                         Современная физическая картина мира

1. Строение Вселенной
2.              Строение Вселенной
3.                         Солнечная система
4.                         Звёзды и источники их энергии. Современные представления о происхождении и эволюции Солнца и звёзд
5.                         Наша галактика и другие галактики
6.                         Пространственные масштабы наблюдаемой Вселенной
7.                         Применимость законов физики для объяснения природы космических объектов
8.                         «Красное смещение» в спектрах галактик
9.                         Современные взгляды на строение и эволюцию Вселенной
10.                         Наблюдение солнечных пятен, звёздных скоплений, туманностей и галактик
11. Медиаматериалы
12. Магнитное поле
13. Дисперсия света
14. Виды излучений и спектры
15. Загадки спектра
16. Инфракрасное и ультрафиолетовое излучение

Источник: http://light-fizika.ru/index.php/11-klass?layout=edit&id=127

Сила Лоренца, определение, формула, физический смысл

Силой Лоренца называют силу, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:

F = q(E+vB),

где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы. 

Сила Лоренца очень похожа по своему принципу на силу Ампера, разница заключается в том, что последняя действует на весь проводник, который в целом электрически нейтральный, а сила Лоренца описывает влияние электромагнитного поля лишь на единичный движущийся заряд.

В природе сила Лоренца позволяет защищать Землю от воздействия космической радиации. Под её воздействием падающие на планету заряженные частицы отклоняются от прямой траектории благодаря присутствию магнитного поля Земли, вызывая полярные сияния.

В технике сила Лоренца используется очень часто: во всех двигателях и генераторах именно она приводит во вращение ротор под действием электромагнитного поля статора.

Таким образом, в любых электромоторах и электроприводах основным видом силы является Лоренцева. Кроме того, она применяется в ускорителях заряженных частиц, а также в электронных пушках, которые раньше устанавливались в ламповых телевизорах. В кинескопе испускаемые пушкой электроны отклоняются под влиянием электромагнитного поля, что происходит при участии Лоренцевой силы.

Кроме того, эта сила используется в масс-спектрометрии и масс-электрографии для приборов, способных сортировать заряженные частицы в зависимости от их удельного заряда (отношение заряда к массе частицы).

Это позволяет с высокой точностью определять массу частиц. Также находит применение в других КИП, например, в бесконтактном способе измерения расхода электропроводящих жидких сред (расходомеры).

Это очень актуально, если жидкая среда обладает очень высокой температурой (расплав металлов, стекла и др.).

Источник: https://pue8.ru/elektrotekhnik/408-sila-lorentsa-opredelenie-formula.html

Сила Лоренца: определение, формулы, правило левой руки

В статье расскажем про магнитную силу Лоренца, как она действует на проводник, рассмотрим правило левой руки для силы Лоренца и момент силы действующий на контур с током.

Сила Лоренца — это сила, которая действует на заряженную частицу, падающую с определенной скоростью в магнитное поле. Величина этой силы зависит от величины магнитной индукции магнитного поля B, электрического заряда частицы q и скорости v, с которой частица падает в поле.

То, как магнитное поле B ведет себя по отношению к нагрузке полностью отличается от того, как это наблюдается для электрического поля Е.

 Прежде всего, поле B не реагирует на нагрузку.

 Однако когда нагрузка перемещается в поле B, появляется сила, которая выражается формулой, которую можно рассматривать как определение поля B:

Таким образом, видно, что поле B выступает в качестве силы, перпендикулярной к направлению вектора скорости V нагрузок и направление вектора B. Это можно проиллюстрировать на диаграмме:

На диаграмме q положительный заряд!

Единицы поля B могут быть получены из уравнения Лоренца. Таким образом, в системе СИ единица B равна 1 тесла (1T). В системе CGS полевой единицей является Гаусс (1G). 1T = 104G

Движение заряда в поле B показано на анимации

Для сравнения показана анимация движения как положительного, так и отрицательного заряда.

Когда поле B охватывает большую площадь, заряд q, движущийся перпендикулярно направлению вектора B, стабилизирует свое движение по круговой траектории. Однако, когда вектор v имеет компонент, параллельный вектору B, тогда путь заряда будет спиралью, как показано на анимации

Сила Лоренца на проводник с током

Сила, действующая на проводник с током, является результатом силы Лоренца, действующей на движущиеся носители заряда, электроны или ионы. Если в разделе направляющей длиной l, как на чертеже

полный заряд Q движется, тогда сила F, действующая на этот сегмент, равна

Частное Q / t является значением протекающего тока I и, следовательно, сила, действующая на участок с током, выражается формулой

Только электроны движутся в металле под действием разности потенциалов; ионы металлов остаются неподвижными в кристаллической решетке. В растворах электролитов анионы и катионы подвижны.

Правило левой руки сила Лоренца

Правило левой руки сила Лоренца — определяющее направление и возврат вектора магнитной (электродинамической) энергии.

Если левая рука расположена так, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (чтобы они проникали внутрь руки), а все пальцы — кроме большого пальца — указывают направление протекания положительного тока (движущаяся молекула), отклоненный большой палец указывает направление электродинамической силы, действующей на положительный электрический заряд, помещенный в это поле (для отрицательного заряда, сила будет противоположная).

Второй способ определения направления электромагнитной силы заключается в расположении большого, указательного и среднего пальцев под прямым углом. При таком расположении указательный палец показывает направление линий магнитного поля, направление среднего пальца — направление движения тока, а также направление большого пальца силы. 

Момент силы, действующий на контур с током в магнитном поле

Момент силы, действующей на контур с током в магнитном поле (например, на проволочную катушку в обмотке электродвигателя), также определяется силой Лоренца. Если петля (отмеченная на схеме красным цветом) может вращаться вокруг оси, перпендикулярной полю B, и проводит ток I, то появляются две неуравновешенные силы F, действующие в стороны от рамы, параллельной оси вращения.

Момент этих сил М

Определим вектор магнитного момента контура

Теперь мы можем сохранить крутящий момент в виде

Эти силы, действующие на элементы петли перпендикулярно оси вращения, направлены и взаимно компенсируются.

Источник: https://meanders.ru/sila-lorenca.shtml

Методическая разработка по физике (9 класс) по теме: Сила Ампера. Сила Лоренца.Правила левой руки. | Социальная сеть работников образования

Мы уже знаем, что магнитное поле образуется вокруг постоянных (природных) магнитов, проводников, по которым течет ток и вокруг движущихся заряженных частиц.

Чтобы отличить это поле от внешнего магнитного поля будем обозначать В0 – вектор магнитной индукции собственного поля и В- вектор магнитной индукции внешнего магнитного поля.

Что будет происходить с магнитом, помещенным во внешнее магнитное поле? Магнит и магнитное поле будут взаимодействовать.

Сила, с которой магнитное поле действует на проводник с током, помещенным в это поле,  называется  силой Ампера.

• Величина силы находится по формуле:
• Fа = I*l*B*sinα  (1)
• Где I- сила тока, А
•         l- длина проводника, м
•         В – вектор магнитной индукции внешнего магнитного поля, Тл.
•         α – угол между вектором магнитной индукции и силой тока.
• Проанализируем эту формулу: сила Ампера прямо пропорциональна току, длине проводника, вектору магнитной индукции внешнего магнитного поля.
• Как влияет угол α на силу Ампера?

Если угол α равен нулю, то магнитное поле не будет действовать на проводник. Если угол будет равен 900, то сила Ампера будет максимальной.

1. Из формулы №1 находят величину вектора магнитной индукции.
2. В= Fа/ I*l* sinα
3. Направление силы Ампера определяется правилом левой руки.
4. Надо расположить левую руку так, чтобы вектор В колол ладонь, 4 пальца показывали направление силы тока, тогда, отогнутый на 900 большой палец покажет направление силы Ампера.
5. Сила, с которой внешнее магнитное поле действует на движущуюся заряженную частицу, попавшую в это магнитное поле, называется силой Лоренца.
6. Fл = q*V*B*sinα  (2)
7.         q — заряд частицы, Кл
8.         V – скорость частицы, м/с
9.         В – вектор магнитной индукции внешнего магнитного поля, Тл.
10.         α – угол между вектором магнитной индукции и скоростью частицы.

Проанализируем эту формулу: сила Лоренца прямо пропорциональна заряду частицы, скорости движения частицы, вектору магнитной индукции внешнего магнитного поля.

Поле не будет действовать на частицу, если та влетела в поле под углом 00, и примет свое максимальное значение, если угол будет равен 900.

Кроме того, при угле 900 сила Лоренца заставит частицу двигаться по окружности и сила Лоренца будет являться центростремительной силой.

• Fл = maц
• Fл = q*V*B
• aц = V2/r       , отсюда mV/r = qB
• Эта формула позволяет найти массу частицы, ее скорость, радиус окружности, по которой она будет двигаться в магнитном поле, заряд частицы, вектор магнитной индукции внешнего поля.
• Для определения направления силы Лоренца используется правило левой руки:

Надо расположить левую руку так, чтобы вектор В колол ладонь, 4 пальца показывали направление скорости частицы, тогда, отогнутый на 900 большой палец покажет направление силы Лоренца. Это правило используют для определения направления положительно заряженной частицы, если частица заряжена отрицательно, то силу перенаправляют в другую сторону.

Сила Лоренца может:

• тормозить частицу,
• разгонять ее,
• двигать по спирали,
• двигать по окружности.

Источник: https://nsportal.ru/shkola/fizika/library/2014/06/09/sila-ampera-sila-lorentsapravila-levoy-ruki

5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях

• Сила,
  действующая на электрический заряд Q,
  движущийся
  в магнитном поле со скоростью v,
  называется силой Лоренца и выражается
  формулой
• (114.1)
• где В — индукция
  магнитного поля, в котором заряд движется.

Направление
силы Лоренца определяется с помощью
правила левой руки: если ладонь левой
руки расположить так, чтобы в нее входил
вектор В, а четыре вытянутых пальца
направить вдоль вектора v
(для Q
> 0направления
I
и v
совпадают, для Q
< 0—
противоположны), то отогнутый большой
палец покажет направление силы,
действующей на положительный
заряд. На
рис. 169 показана взаимная ориентация
векторов v,
В (поле направлено к нам, на рисунке
показано точками) и F
для положительного заряда. На отрицательный
заряд сила действует в противоположном
направлении. Модуль силы Лоренца (см.
(114.1)) равен

где

— угол между v
и В.

Выражение
для силы Лоренца (114.1) позволяет найти
ряд закономерностей движения заряженных
частиц в магнитном поле. Направление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака заряда
Qчастицы.
На этом основано определение знака
заряда частиц, движущихся в магнитных
полях.

Если
заряженная частица движется в магнитном
поле со скоростью v,
перпендикулярной вектору В, то сила
Лоренца F
= Q[vB]
постоянна по модулю и нормальна к
траектории частицы.

Согласно второму
закону Ньютона, эта сила создает
центростремительное ускорение.

Отсюда
следует, что частица будет двигаться
по окружности, радиус rкоторой
определяется из условия QvB
= mv2/r,откуда

(115.1)

Период
вращения частицы, т.
е. время Т,
за
которое она совершает один полный
оборот,

Подставив
сюда выражение (115.1), получим

(115.2)

т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду
(Q/m)
частицы, и магнитной индукцией поля, но
не зависит от ее скорости (при v≪c).
На
этом основано действие циклических
ускорителей заряженных частиц (см. §
116).

Если
скорость v
заряженной частицы направлена под углом

к вектору В (рис.

170), то ее движение можно
представить в виде суперпозиции: 1)
равномерного прямолинейного движения
вдоль поля со скоростью v1
= vcos;
2) равномерного движения со скоростью
v=
vsin
по окружности в плоскости, перпендикулярной
полю.

Радиус окружности определяется
формулой (115.1) (в данном случае надо
заменить vна
v=
vsin).
В результате сложения обоих движений
возникает движение по спирали, ось
которой параллельна магнитному полю
(рис. 170).

Рис.
170

Шаг
винтовой линии

Подставив в
последнее выражение (115.2), получим

Направление, в
котором закручивается спираль, зависит
от знака заряда частицы.

Если
скорость т заряженной частицы составляет
угол а с направлением вектора В
неоднородного
магнитного
поля, индукция которого возрастает в
направлении движения частицы, то г и А
уменьшаются с ростом В.
На
этом основана фокусировка заряженных
частиц в магнитном поле.

Источник: https://studfile.net/preview/6447629/page:3/