Умножение матрицы на вектор, формула и примеры

netlib.narod.ru

В этом разделе мы сосредоточимся на математике матриц. Их использование в трехмерной компьютерной графике будет рассмотрено в следующем разделе.

Матрицей m × n называется прямоугольный массив чисел, состоящий из m строк и n столбцов. Количество строк и столбцов определяет размер матрицы.

Отдельный элемент матрицы идентифицируется путем указания его строки и столбца в состоящем из двух элементов спсике индексов; первый индекс определяет строку, а второй — столбец.

Ниже в качестве примера приведены матрицы M размером 3 × 3, В размером 2 × 4 и С размером 3 × 2:

В большинстве случаев для обозначения матриц мы будем использовать заглавные полужирные буквы. Иногда матрицы состоят из единственной строки или единственного столбца. Чтобы отличать такие матрицы, мы дадим им специальные имена: вектор-строка (row vector) и вектор-столбец (column vector). Вот примеры таких векторов:

Для элементов вектора-строки и вектора-столбца необходим только один индекс. Иногда для идентификации элемента строки или столбца в качестве индекса мы будем использовать буквы.

Равенство, умножение матрицы на скаляр и сложение матриц

Для пояснения рассматриваемых терминов в данном разделе будут использованые следующие четыре матрицы:

• Две матрицы считаются равными, если они имеют одинаковую размерность и их соответствующие элементы равны. Например, A = C, поскольку матрицы A и C имеют одинаковую размерность и их соответствующие элементы равны. Мы говорим, что A ≠ B и A ≠ D поскольку у этих матриц либо разная размерность, либо не равны соответствующие элементы.
• Мы можем умножить матрицу на скаляр для чего нам необходимо умножить каждый элемент матрицы на данный скаляр. Например, умножив D на скаляр k получим: Если k = 2, получим:
• Можно сложить две матрицы, но только в том случае, если у них одинаковая размерность. Сумма вычисляется путем сложения соответствующих элементов матриц. Например:
• Аналогично сложению можно выполнять вычитание двух матриц, имеющих одинаковую размерность. Вычитание матриц иллюстрирует следующий пример:

Умножение

Умножение матриц это наиболее важная операция, которая постоянно используется в трехмерной компьютерной графике. Именно умножение матриц позволяет осуществлять преобразование векторов и комбинировать несколько преобразований в одно. Преобразования будут рассмотрены в следующем разделе.

Чтобы получить произведение матриц AB необходимо чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы A и B, с размерностью 2 × 3 и 3 × 3 соответственно:

Как видите, произведение AB определено поскольку количество столбцов матрицы A равно количеству строк матрицы B.

Обратите внимание, что произведение BA, получаемое в результате перестановки множителей, не определено, потому что количество столбцов матрицы B не равно количеству строк матрицы A.

Это говорит о том, что в обшем случае операция умножения матриц не коммутативна (то есть AB ≠ BA). Мы говорим «в общем случае не коммутативна» по той причине, что существует ряд частных случаев в которых операция умножения матриц ведет себя как коммутативная.

После того, как мы узнали в каких случаях произведение матриц определено, можно дать определение операции умножения матриц: если A — это матрица m × n, а B — матрица n × p, то их произведением будет матрица C, размером m × p, в которой элемент cij находится как скалярное произведение i-го вектора-строки матрицы A и j-го вектора-столбца матрицы B:

В этой формуле ai обозначает i-ый вектор-строку в матрице A, а bj — j-ый вектор-столбец матрицы B.

Давайте для примера вычислим произведение:

Произведение определено, поскольку количество столбцов матрицы A равно количеству строк матрицы B. Кроме того, обратите внимание, что размер полученной в результате матрицы — 2 × 2. Согласно формуле (4) получаем:

В качестве упражнения проверьте, что в данном случае AB ≠ BA.

И еще один, более общий, пример:

Единичная матрица

Существует особая матрица, называемая единичной матрицей (identity matrix). Это квадратная матрица все элементы которой равны нулю, за исключением тех, что расположены на главной диагонали — эти элементы равны единице. Ниже приведены примеры единичных матриц размером 2 × 2, 3 × 3 и 4 × 4:

Единичная матрица действует как мультипликативное тождество:

Следовательно, операция умножения на единичную матрицу не изменяет исходную матрицу. Более того, умножение на единичную матрицу это один из случаев, когда операция умножения матриц является коммутативной. Вы можете думать о единичной матрице как о числе 1 для матриц.

ПРИМЕР

Проверьте, что в результате умножения матрицы М = на единичную матрицу размером 2 × 2 получается матрица М.

Инвертирование матриц

В математике матриц нет аналога операции деления, но зато есть мультипликативная операция инвертирования. Приведенный ниже список обобщает важные особенности инвертирования:

• Инвертировать можно только квадратные матрицы, так что когда мы говорим об инвертировании матрицы, подразумевается, что мы имеем дело с квадратной матрицей.
• В результате инвертирования матрицы M размером n × n получается матрица размером n × n, которую мы будем обозначать M-1.
• Не всякую квадратную матрицу можно инвертировать.
• Если перемножить исходную и инвертированную матрицы, получится единичная матрица: MM-1 = M-1M = I. Обратите внимание, что в случае перемножения исходной и инвертированной матриц операция умножения матриц коммутативна.

Инверсия матриц применяется для нахождения искомой матрицы в уравнениях. Для примера возьмем выражение p' = pR и предположим, что нам известны p' и R, а требуется найти p. Сначала вычислим R-1 (подразумевается, что эта матрица существует). Получив R-1 можно вычислить p по следующему алгоритму:

Описание способа вычисления инвертированной матрицы выходит за рамки этой книги, но вы можете его найти в любом учебнике линейной алгебры. В разделе «Базовые преобразования» мы получим инверсию нескольких матриц, с которыми будем работать. В раздеде «Матрицы в библиотеке D3DX» мы познакомимся с функцией библиотеки D3DX, которая может инвертировать матрицу за нас.

Завершая раздел об инвертировании матриц представим вам одно полезное свойство, касающееся инвертирования произведения: (AB)-1 = B-1A-1. Здесь подразумеваеся, что матрицы A и B могут быть инвертированы и что обе они — квадратные матрицы одинакового размера.

Транспонирование матриц

Транспонирование матрицы осуществляется путем перестановки ее строк и столбцов. Следовательно, результатом транспонирования матрицы m × n будет матрица n × m. Результат транспонирования матрицы M мы будем обозначать MT.

ПРИМЕР

Транспонируйте следующие две матрицы: Напомним, что транспонирование матрицы осуществляется путем перестановки ее строк и столбцов. Следовательно:

Матрицы в библиотеке D3DX

Программируя приложения Direct3D мы чаще всего будем использовать матрицы 4 × 4 и векторы-строки 1 × 4. Обратите внимание, что использование матриц двух указанных размеров подразумевает, что определены результаты следующих операций умножения матриц:

• Умножение вектора-строки на матрицу. То есть, если v — это вектор-строка 1 × 4, а T — это матрица 4 × 4, произведение vT определено и представляет собой вектор-строку 1 × 4.
• Умножение матрицы на матрицу. То есть, если T — это матрица 4 × 4 и R — это матрица 4 × 4, произведения TR и RT определены и оба являются матрицами 4 × 4. Обратите внимание, что произведение TR не обязательно равно RT, поскольку операция умножения матриц не коммутативна.

Для представления вектора-строки 1 × 4 в библиотеке D3DX, мы будем использовать классы векторов D3DXVECTOR3 и D3DXVECTOR4. Конечно, в классе D3DXVECTOR3 только три компоненты, а не четыре. Однако обычно подразумевается что четвертая компонента равна нулю или единице (более подробно это будет обсуждаться в следующем разделе).

Для представления матриц 4 × 4 в библиотеке D3DX, мы используем класс D3DXMATRIX, определение которого выглядит следующим образом:

typedef struct D3DXMATRIX : public D3DMATRIX
{
public:
D3DXMATRIX() {};
D3DXMATRIX(CONST FLOAT*);
D3DXMATRIX(CONST D3DMATRIX&);
D3DXMATRIX(FLOAT _11, FLOAT _12, FLOAT _13, FLOAT _14,
FLOAT _21, FLOAT _22, FLOAT _23, FLOAT _24,
FLOAT _31, FLOAT _32, FLOAT _33, FLOAT _34,
FLOAT _41, FLOAT _42, FLOAT _43, FLOAT _44);

// получение элемента
FLOAT& operator () (UINT Row, UINT Col);
FLOAT operator () (UINT Row, UINT Col) const;

// приведение типа
operator FLOAT* ();
operator CONST FLOAT* () const;

// операторы присваивания
D3DXMATRIX& operator *= (CONST D3DXMATRIX&);
D3DXMATRIX& operator += (CONST D3DXMATRIX&);
D3DXMATRIX& operator -= (CONST D3DXMATRIX&);
D3DXMATRIX& operator *= (FLOAT);
D3DXMATRIX& operator /= (FLOAT);

// унарные операторы
D3DXMATRIX operator + () const;
D3DXMATRIX operator — () const;

// бинарные операторы
D3DXMATRIX operator * (CONST D3DXMATRIX&) const;
D3DXMATRIX operator + (CONST D3DXMATRIX&) const;
D3DXMATRIX operator — (CONST D3DXMATRIX&) const;
D3DXMATRIX operator * (FLOAT) const;
D3DXMATRIX operator / (FLOAT) const;

friend D3DXMATRIX operator * (FLOAT, CONST D3DXMATRIX&);

BOOL operator == (CONST D3DXMATRIX&) const;
BOOL operator != (CONST D3DXMATRIX&) const;
} D3DXMATRIX, *LPD3DXMATRIX;

Класс D3DXMATRIX наследует элементы данных от простой структуры D3DMATRIX, определенной следующим образом:

typedef struct _D3DMATRIX {
union {
struct {
float _11, _12, _13, _14;
float _21, _22, _23, _24;
float _31, _32, _33, _34;
float _41, _42, _43, _44;
};
float m[4][4];
};
} D3DMATRIX;

D3DXMATRIX A(Е); // инициализация A
D3DXMATRIX B(Е); // инициализация B
D3DXMATRIX C = A * B; // C = AB

Другим важным оператором класса D3DXMATRIX являются скобки, позволяющие легко получить доступ к отдельным элементам матрицы. Обратите внимание, что при использовании скобок нумерация элементов матрицы начинается с нуля, подобно нумерации элементов массива в языке С. Например, чтобы обратиться к верхнему левому элементу матрицы, следует написать:

D3DXMATRIX M;
M(0, 0) = 5.0f; // Присвоить первому элементу матрицы значение 5.0f.

Кроме того, библиотека D3DX предоставляет набор полезных функций, позволяющих инициализировать единичную матрицу D3DXMATRIX, транспонировать матрицу D3DXMATRIX и инвертировать матрицу D3DXMATRIX:

D3DXMATRIX *D3DXMatrixIdentity(
D3DXMATRIX *pout // Матрица, инициализируемая как единичная
);

D3DXMATRIX M;
D3DXMatrixIdentity(&M); // M = единичная матрица

D3DXMATRIX *D3DXMatrixTranspose(
D3DXMATRIX *pOut, // Результат транспонирования матрицы
CONST D3DXMATRIX *pM // Транспонируемая матрица
);

D3DXMATRIX A(…); // инициализация A
D3DXMATRIX B;
D3DXMatrixTranspose(&B, &A); // B = транспонированная(A)

D3DXMATRIX *D3DXMatrixInverse(
D3DXMATRIX *pOut, // возвращает результат инвертирования pM
FLOAT *pDeterminant, // детерминант, если необходим, иначе 0
CONST D3DXMATRIX *pM // инвертируемая матрица
);

Функция инвертирования возвращает NULL, если переданная ей матрица не может быть инвертирована. Кроме того, в этой книге мы игнорируем второй параметр и всегда передаем в нем 0.

D3DXMATRIX A(…); // инициализация A
D3DXMATRIX B;
D3DXMatrixInverse(&B, 0, &A); // B = инвертированная(A)

netlib.narod.ru

Сайт управляется системой uCoz

Источник: http://netlib.narod.ru/library/book0032/part1_02.htm

1_Вычисления в Excel. Учебное пособие Набережные Челны 2003 г

Подборка по базе: Тесты по общей хирургии (полный вариант), 2003.doc, Миома тела матки методическое пособие.doc, Ананьев В.П., Потапов А.Д. Инженерная геология Пособие.djvu, Электроника и электротехника. Наглядное пособие.

pdf, Методическое пособие по организации самостоятельной работы студе, Учебное пособие для студентов высших технических учебных заведен, вышкомонтажные работы пособие.pdf, Учебное пособие (к диплому).pdf, Учебное пособие Ценообразование АО.doc, Методическое пособие Организация проверок эксплуатации лифтов.

pd Векторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец).

• сложение — два вектора а и b с одинаковым числом компо­нент образуют новый вектор с: сi = ai + bi ;
• умножение на число — каждая компонента вектора умножает­ся на число, т.е. b = λа означает bi = λаi

здесь i — номер компоненты вектора.

Упражнение 6.1.1. Сложить два вектора:

1. Ввести в первую строку вектор Х — (А1:Е1)
2. Ввести во вторую строку вектор Y — (А2:Е2)
3. Найти сумму векторов –

• выделить блок ячеек для результата в третьей строке (А3:Е3);
• ввести в строке формул =А1:Е1+А2:Е2
• нажать Ctrl+Shift+Enter.

Иллюстрация к примеру — рис. 14.А В С D E23Рис. 14. Иллюстрация к упражнению 6.1.1.

Задача 6.1.1. Умножить вектор на число.

Упражнение 6.1.2.

Умножение вектор-столбца на вектор-строку.

Решение.

1-й способ: за­писать в ячейку В2 формулу =$А2*В$1 и скопировать ее в ос­тальные ячейки диапазона B2:D5.

2 -й способ (более экономный): выделить блок B2:D5. За­пишем в него формулу массива {=А2:А5*B1:D1}.

Анализ решения. Табличный массив {2;-3;4} — вектор-строка, а блок А2:А5 — вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).

Примечание. Если ввести формулу {=B1:D1* А2:А5}, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомно­жителе должно равняться числу строк во втором сомножителе).

Упражнение 6.1.3. Вычислить скалярное произведение двух векторов.

1. Установить курсор в ячейку, где нужен результат.
2. Щёлкнуть кнопку автосуммы — .
3. Выделить массив Х (А5:А12).
4. Нажать знак умножить —*.
5. Выделить массив Y (B5:B12).
6. Нажать Ctrl + Shift + Enter.

Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12). Простейшие операции, которые можно проделывать с мат­рицами: сложение (вычитание), умножение на число, перемно­жение, транспонирование, вычисление обратной матрицы.

Упражнение 6.2.1. Сложение матриц.

Задание. Сло­жить матрицы М и N, где

Решение.

M= и N=

1-й способ:

• Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2.
• В блок А4:С5 ввести табличную формулу {= А1:С2 + E1:G2}.

Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.

2-й способ:

Использование имен делает процедуру ввода табличной формулы намного проще:

• Задать диапазонам А1:С2 и E1:G2 имена М и N.
• В блок E4:G5 ввести табличную формулу { = М + N }.

Результат, естественно, тот же: M+N =

Упражнение 6.2.2. Вычислить линейную комбинацию матриц 2*М — N (матрицы М.и N из упражнения 6.2.1.).

Решение. В блок А7:С8 ввести табличную формулу {= 2*М — N }.

Результат: 2*M — N =

Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложе­нии матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сло­жение.

• Для матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»:
• МОПРЕД — вычисление определителя матрицы;
• МОБР — вычисление обратной матрицы;
• МУМНОЖ — перемножение матриц;
• ТРАНСП — транспонирование.

Примечание. Первая из этих функций возвращает число, поэтому вводит­ся как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.

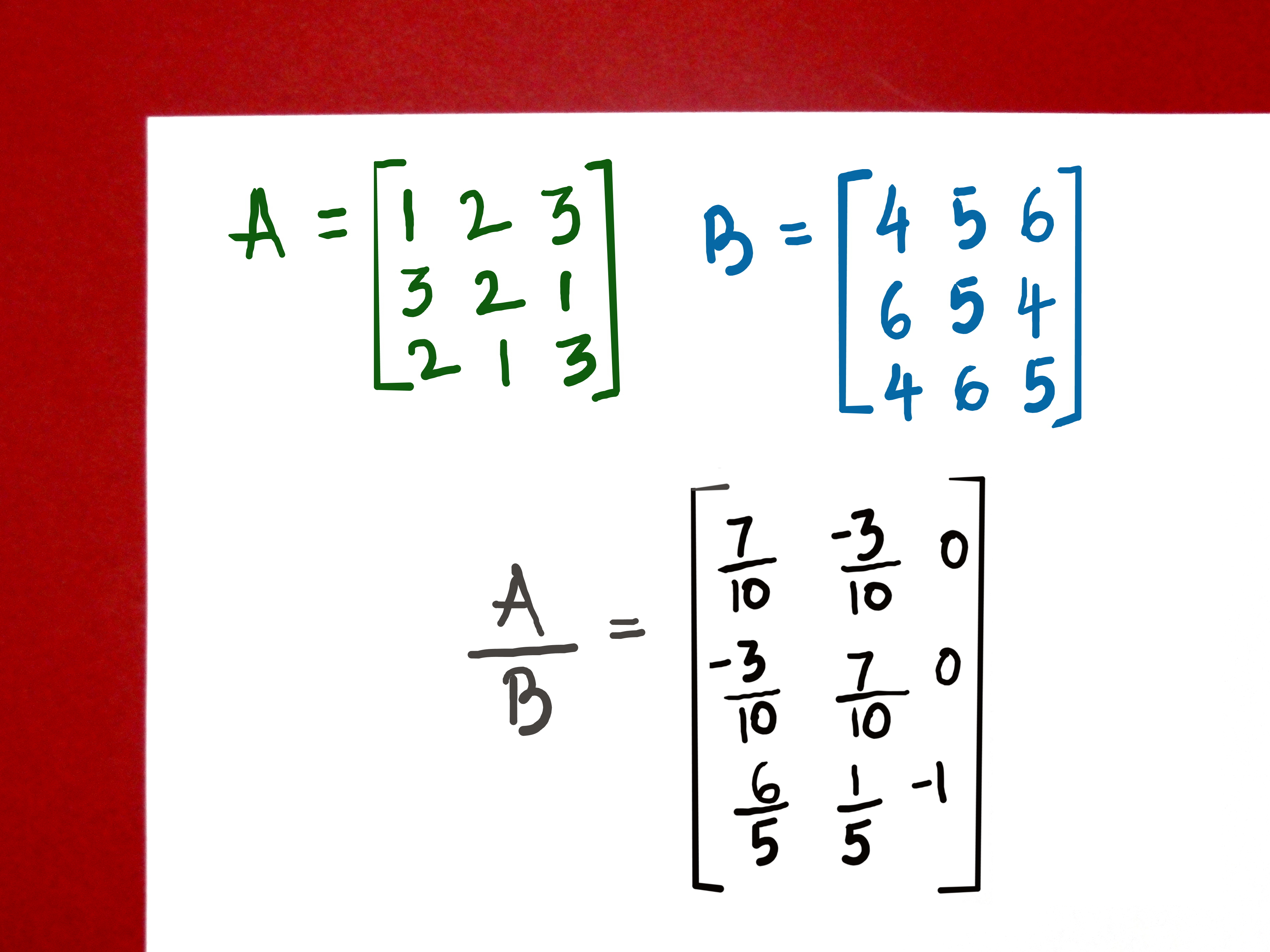
Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:

А =

Решение. Разместить исходную матрицу в блоке А1 :СЗ.

1. В ячейке Е2 поместить формулу для вычисления определи­теля = МОПРЕД (А1:СЗ).
2. В блок А5:С7 ввести формулу для вычисления обратной матрицы:

Примечания:

Источник: https://topuch.ru/uchebnoe-posobie-naberejnie-chelni-2003-g/index10.html

Как умножить вектор на матрицу

В теории матриц вектором называется матрица, имеющая только один столбец или только одну строку. Умножение такого вектора на другую матрицу происходит по общим правилам, однако имеет и свои особенности. По определению произведения матриц умножение возможно только в том случае, если количество столбцов первого множителя равно количеству строк второго. Следовательно, вектор-строку удастся умножить только на матрицу, в которой столько же строк, сколько элементов в вектор-строке. Аналогично, вектор-столбец можно умножить только на матрицу, в которой столько же столбцов, сколько элементов в вектор-столбце. Умножение матриц некоммутативно, то есть если A и B — матрицы, то A*B ≠ B*A. Более того, существование произведения A*B вовсе не гарантирует существования произведения B*A. Например, если матрица A имеет размеры 3*4, а матрица B — 4*5, то произведение A*B — матрица размером 3*5, а B*A не определено. Пусть задан: вектор-строка A = [a1, a2, a3 … an] и матрица B размерности n*m, элементы которой равны:[b11, b12, b13, … b1m;b21, b22, b23, … b2m;…

bn1, bn2, bn3, … bnm].

Тогда произведение A*B будет вектор-строкой размерности 1*m, причем каждый элемент ее равен:Cj = ∑ai*bij (i = 1 … n, j = 1 … m).

Иными словами, для нахождения i-того элемента произведения нужно умножить каждый элемент вектора-строки на соответствующий ему по порядку элемент i-того столбца матрицы и просуммировать эти произведения.

Аналогично, если задана матрица A размерности m*n и вектор-столбец B размерности n*1, то их произведение будет вектором-столбцом размерности m*1, i-тый элемент которого равен сумме произведений элементов вектора-столбца B на соответствующие им элементы i-той строки матрицы A. Если A — вектор-строка размерности 1*n, а B — вектор-столбец размерности n*1, то произведение A*B является числом, равным сумме произведений соответствующих элементов этих векторов:c = ∑ai*bi (i = 1 … n).

Это число называется скалярным, или внутренним, произведением.

Результат умножения B*A в этом случае является квадратной матрицей размерности n*n. Ее элементы равняются:Cij = ai*bj (i = 1 … n, j = 1 … n).

Такая матрица называется внешним произведением векторов.

• Войти на сайт
• или

Источник: https://www.kakprosto.ru/kak-81801-kak-umnozhit-vektor-na-matricu

Умножение матрицы на вектор — Энциклопедия по экономике

Умножение матрицы на вектор

При умножении матрицы на вектор-столбец мы умножаем все элементы первого столбца матрицы на первый элемент вектора, все элементы второго столбца матрицы на второй элемент вектора, и так далее.

Если бы вектор был вектор-строка, мы бы умножили все элементы первой строки матрицы на первый элемент вектора, все элементы второй строки матрицы на второй элемент вектора, и так далее.

Так как речь идет о векторе-столбце и последние четыре элемента нули, нам надо умножить первый столбец обратной матрицы на Е (ожидаемая прибыль портфеля) и второй столбец обратной матрицы на S (сумма весов). Мы получим следующий набор уравнений, в которые можно подставить значения Е и S и получить оптимальные веса.
 [c.201] Блочный алгоритм умножения матрицы на вектор.
 [c.

157]

На рис. 1.52 построены графики зависимости ускорения S от времени т передачи единицы информации по каналам связи в ВС при р = 8. Вполне естественно, что с ростом т ускорение стремится к 1, так как в общем времени выполнения алгоритма возрастает доля обменов по сравнению со временем вычислений. Вместе с тем для разных методов ускорение падает по-разному.

Наилучший результат, опять же, наблюдается для метода умножения матрицы на вектор. Наиболее чувствительны к этому параметру оказались методы L[/-разложения и декомпозиции области решения трех-диагональных систем. Величина ускорения S при т — 0 обусловлена только балансировкой вычислительной нагрузки процессоров, так как соответствует ситуации, когда время на выполнение обменов стремится к 0.
 [c.158]

Умножение матрицы на вектор
 [c.56]

Операция умножения матриц часто используется в матричной алгебре и ее приложениях для преобразования и выделения необходимых элементов, строк или столбцов матрицы. Это достигается умножением матрицы на специально подобранную матрицу или вектор.
 [c.387]

Таким образом, чтобы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу его нужно рассматривать как вектор-строку. .  [c.56]

Умножение матрицы А на вектор Y Y = AY.  [c.161]

X ТА] — это обратная к матрице, получающейся от умножения транспонированной из X матрицы, на матрицу X. Эта обратная матрица снова умножается на транспонированную из X, а произведение умножается на вектор Y.
 [c.310]

Здесь мы умножим матрицу С на вектор, чтобы получить новый вектор. Такой же вектор мы получим при умножении 0,000271 на первоначальный вектор. Таким образом, мы видим, что вектор в левой части — это собственный вектор, и скаляр 0,000271 — это собственное значение.
 [c.499]

Вектор-столбец кредитовых оборотов получаем умножением матрицы кредитовых оборотов, т. е. транспонированной матрицы, на оператор выделения итогового столбца  [c.122]

Само число не имеет позиции, оно является скалярной величиной, но при умножении на матрицу (или вектор) число занимает в ней определенную позицию и становится его элементом, как, например, при умножении на матрицу и вектор специального вида  [c.385]

Таким образом, при умножении слева на единичную вектор-строку получаем вектор-строку, состоящую из итогов столбцов матрицы А.
 [c.389]

Коэффициенты полных затрат связаны с конечным продуктом, т. е. с той частью продукции, которая используется на непроизводственное потребление, накопление и другие конечные расходы общества.

Если матрицу (таблицу) коэффициентов полных затрат умножить на вектор конечного продукта, то получим объем в ало-вых выпусков каждой отрасли. Умножение выполняется согласно математическим правилам.

Подробнее этот вопрос рассматривается в 32.5.
 [c.501]

В настоящее время разработан ряд методов исчисления обратных матриц и, следовательно, получения коэффициентов полных затрат. Среди них можно выделить два основных способа обращения матриц, основанные на итерационных методах (методах последовательного приближения) и на использовании метода прямого обращения матриц.

При итерационном методе многократно повторяются однотипные вычисления, постепенно приближающиеся к искомому результату. При втором способе расчеты сводятся к решению системы уравнений и нахождению коэффициентов полных затрат путем инверсии (обращения) матрицы коэффициентов прямых затрат.

Так, матрица коэффициентов полных затрат, умноженная на вектор конечной продукции, дает объем производства продукции по каждой отрасли. Расчет осуществляется по следующей формуле  [c.507]

Аналогично при умножении матрицы А на вектор-строку (слева) Ь А мы получаем вектор-строку, являющийся линейной комбинацией строк матрицы А с коэффициентами .
 [c.492]

Вычитание из каждой строки матрицы L ее элемента, стоящего на главной диагонали, дает матрицу риска Z°. Сформировав 10-мерный вектор Р априорных вероятностей, пропорциональных длинам интервалов разбиения, получаем вектор ожидаемого риска R° — Z° х Р. Его составляющие 24.38, 20.62, 18.47, 23.20, 36.16, 58.10, 89.21, 129.

23, 177.63, 233.41. Минимальная составляющая г° — 18.47 указывает на целесообразность выбора s , связанного с третьим интервалом, т.е. 5 —1 штукам. Ожидаемые затраты могут быть получены умножением вектор-столбца матрицы затрат, соответствующего s — s , на вектор-строку вероятностей Р и в данном случае составляют 148.47 руб.
 [c.

299]

После перестановки и умножения на матрицу, обратную матрице дисперсии и ковариации, оптимальный вектор портфеля описывается через
 [c.197]

Xit то это равно умножению вектора на скалярную величину Я г, т. е. СХ. = Я X.. Симметричность матрицы С означает, что существует N таких векторов (при условии, что С — это не невырожденная матрица, т. е. обладает обратной матрицей) и что они ортогональны.
 [c.303]

Мы можем доказать, что полученные векторы являются собственными векторами, потому что собственные векторы — это векторы, которые при умножении на матрицу С равны произведению вектора на скалярную величину. Например
 [c.499]

Первый вариант нами был только что рассмотрен. В его условиях итоговые столбцы и строки получаются умножением на единичный вектор того же размера, соответственно, справа или слева от матрицы  [c.398]

Из матрицы сводных проводок S путем ее умножения на специальный вектор-столбец ет + 1, у которого последний m + 1 — элемент равен нулю, а все остальные равны нулю, выделяем вектор-столбец дебетовых оборотов  [c.402]

Из транспонированной матрицы сводных проводок S путем ее умножения на специальный вектор-столбец em +, выделяем вектор-столбец кредитовых оборотов  [c.402]

Здесь (А А) 1 — матрица, обратная к (АТА), то есть такая, которая при умножении на матрицу (АТЛ) дает единичную матрицу. Таким образом, мы получили формулу расчета вектора коэффициентов регрессии в векторно-матричной записи.
 [c.311]

Поставленную задачу можно решить, если использовать умножение матрицы на специальный вектор, называемый еще оператором выделения, в данном случае это оператор выделения итоговоРЬ столбца ешм. Вектор e f -это вектор-столбец, во всех позициях которого находятся нули, кроме последней m + 1, в которой находится 1 (подробности см. в Математическом приложении в конце настоящей книги).
 [c.121]

Если мы предполагаем, что доли ценных бумаг в портфеле равны, то дисперсия портфеля будет определяться умножением матрицы С на горизонтальный вектор весов 1 х N и затем доумножением полученной матрицы на вертикальный вектор весов (N х 1). Таким образом, будем иметь  [c.300]

Од и 1 ко для чюбои матрицы существует набор основны векторов таких, что произведение ма рнцы на вектор из такою набора равносиль но умножению этого вектора ш определенное ч не го
 [c.25]

Источник: https://economy-ru.info/info/197684/