Подготовка к ЕГЭ по математике
Эксперимент
Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами.
- Теория
- Конспект урока
- На предыдущих уроках мы обсуждали показательную функцию, решение показательных уравнений и неравенств.
- Когда мы обсуждали решение показательных уравнений, то нам всегда удавалось представить обе части в виде степеней с одинаковыми основаниями.
Но вполне логично, что может возникнуть ситуация, когда это сделать не удастся. Например, решить уже рассмотренными методами уравнение не получится, так как 5 мы пока не умеем представлять в виде степени с основанием 2.
С другой стороны, мы обсуждали тот факт, что показательная функция принимает любое положительное значение. Поэтому, в какой-то точке значение функции должно равняться 5.
Фактически, мы столкнулись с ситуацией, похожей на извлечение корня – мы точно знали, что есть число, квадрат которого равен 2, но не могли записать его доступными нам методами. В том случае мы поступили следующим образом: ввели новое понятие «корень» и операцию извлечение корня, которая была обратна возведению в степень.
Возвращаясь к нашей проблеме, нам придётся поступить аналогично. Обозначим степень, в которую надо возвести 2, чтобы получить 5, как – логарифм пяти по основанию 2.
То есть, определение логарифма следующее: для ![]() . То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().
. То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().
- Рассмотрим простейшие примеры вычисления логарифмов:
- 1) , так как .
- 2) , так как .
- 3) , так как .
- 4), так как .
- Существует два специальных вида логарифмов: десятичный и натуральный.
Десятичный логарифм – это логарифм с основанием 10. Он обозначается следующим образом: .
Натуральный логарифм – это логарифм с основанием (напомним, что ). Он обозначается следующим образом: .
Исходя из определения логарифма ![]() , легко получить следующее свойство, которое называется основным логарифмическим тождеством. Для этого достаточно подставить вторую формулу в первую. В результате получаем: .
, легко получить следующее свойство, которое называется основным логарифмическим тождеством. Для этого достаточно подставить вторую формулу в первую. В результате получаем: .
Это выражение называется основным логарифмическим тождеством.
Давайте сформулируем ещё несколько основных свойств логарифмов (![]() ).
).
1) (т.к. ),
2) ![]()
![]()
![]()
![]()
5) Формула перехода к новому основанию: ![]()
![]()
![]()
7) (т.к. )
- На этом уроке мы с вами сформулировали определение логарифма, основное логарифмическое тождество и свойства логарифма.
- В практической части урока мы научимся вычислять различные логарифмы, а также преобразовывать выражения, содержащие логарифмы.
- Полезные ссылки:
- 1) Алгебра 11 класс: «Понятие логарифма»
- 2) Алгебра 11 класс: «Понятие логарифма. Простейшие задачи»
- 3) Алгебра 11 класс: «Свойства логарифмов. Логарифм произведения и частного»
- 4) Алгебра 11 класс: «Свойства логарифмов. Логарифм степени»
- 5) Алгебра 11 класс: «Свойства логарифмов. Решение более трудных задач»
- 6) Алгебра 11 класс: «Переход к новому основанию логарифма»
- 7) Алгебра 11 класс: «Переход к новому основанию логарифма. Решение задач»
Источник: https://interneturok.ru/lesson/algebra/11-klass/bzadachi-iz-egeb/urok-3-logarifm-svoystva-logarifmov-vyrazheniya-s-logarifmami-teoriya
Пособие для обучающихся "Формулы и свойства логарифмов"
- Государственное образовательное учреждение
- среднего профессионального образования
- Тульской области
- «Алексинский машиностроительный техникум»
- Формулы и свойства
-
 логарифмов
логарифмов - Разработан
- преподавателем
- математики
Христофоровой М.Ю.
- Определение
- Логарифмом числа b по основанию α (loqαb) называется такое число c, что b = αc, то есть записи loqαb = c и b = αc равносильны.
- Логарифм числа b по основанию α определяется как показатель степени, в которую надо возвести число α, чтобы получить число b.
- Логарифм в переводе с греческого буквально означает «число, изменяющее отношение».
- Обозначение логарифма: loqαb
- Произносится: «логарифм b по основанию α».
- Логарифм имеет смысл, если α >0, α ≠1, b >0.
- Правило о знаке логарифма:
- — если основание α логарифма и число b расположены на числовой оси по одну сторону от 1, то loqαb положителен.
- — если основание αлогарифма и числоb расположены на числовой оси по разные стороны от 1, то loqαb отрицателен.
- Логарифм существует только у положительных чисел.
- Вычисление логарифма называется логарифмированием.
- Числа α , b чаще всего вещественные, но существует также теория комплексных логарифмов
- Специальные обозначения:
-
Натуральный логарифм ln α — логарифм по основанию e, где e — число Эйлера.
-
Десятичный логарифм lq α — логарифм по основанию 10.
- Производная логарифмической функции равна:
-

- Интеграл от логарифма вычисляется интегрированием по частям:
-

- Свойства логарифмов:
- 1° — основное логарифмическое тождество.
- 2°

- 3°

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю, т.к. из любого действительного числа можно получить 1 только возведя его в нулевую степень.
- 4°
 — логарифм произведения.
— логарифм произведения. - Логарифм произведения равен сумме логарифмов сомножителей.
- 5°
 — логарифм частного.
— логарифм частного. - Логарифм частного (дроби) равен разности логарифмов сомножителей.
- 6°
 — логарифм степени.
— логарифм степени. - Логарифм степени равен произведению показателя степени на логарифм ее основания.
- 7°

- 8°
- 9° — переход к новому основанию.
- Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:
- Это тождество сразу получается, если в логарифме слева заменить основание на по вышеприведённой формуле замены основания. Следствия:
- Ещё одно полезное тождество:
- Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию .
- Она определена при .
- Область значений: .
- Эта кривая часто называется логарифмикой.
- Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.
- Функция является строго возрастающей при и строго убывающей при .
График любой логарифмической функции проходит через точку . Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.
Логарифм является монотонной функцией, поэтому экстремумов не имеет.
Ось ординат () является левой вертикальной асимптотой
Из определения следует, что логарифмическая зависимость есть обратная функция для показательной функции , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок).
- Как и показательная, логарифмическая функция относится к категории трансцендентных функций.
Источник: https://infourok.ru/posobie-dlya-obuchayuschihsya-formuli-i-svoystva-logarifmov-557939.html
Свойства логарифмов
- Вопросы занятия:
- · рассмотреть свойства логарифмов;
- · подробно рассмотреть примеры, в которых необходимо преобразовать выражения с логарифмами.
- Материал урока
- Прежде чем приступить к изучению новой темы, давайте повторим определение логарифма, основное логарифмическое тождество:
![]()
![]()
Эти знания нам пригодятся на сегодняшнем уроке.
Сегодня мы рассмотрим основные свойства операции логарифмирования. Заметим, что все свойства мы будем формулировать только для положительных значений переменных, содержащихся под знаком логарифма.
- Итак, первое свойство формулируется следующей теоремой:
- Теорема 1.
- Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, то есть справедлива следующая формула:
![]()
Давайте докажем эту теорему.
Введём следующие обозначения.
Нам надо доказать, что выполняется равенство:
Применим определение логарифма.
По свойству произведения степеней с одинаковыми основаниями получим:
![]()
Поскольку степени двух положительных чисел равны и основания степеней равны и отличны от единицы, то равны и показатели степеней. Значит:
![]()
Что и требовалось доказать.
Рассмотрим пример.

- Сформулируем следующее свойство логарифмов.
- Теорема 2.
- Если а, b, c – положительные числа, причём a ≠ 1, то справедливо равенство:

Другими словами, логарифм частного равен разности логарифмов делимого и делителя.
Или: логарифм дроби равен разности логарифмов числителя и знаменателя.
Эта теорема доказывается аналогично предыдущей. Поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
- Рассмотрим пример.
- Сформулируем следующее свойство.
- Теорема 3.
- Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
- Другими словами, логарифм степени равен произведению показателя степени на логарифм основания степени.
- Эта теорема доказывается аналогично предыдущим, поэтому вы можете доказать её самостоятельно, воспользовавшись свойствами степеней.
- Рассмотрим пример.
- Сформулируем следующее свойство.
- Свойство.
- Если а и b – положительные числа, причём, a ≠ 1, то для любого числа r справедливо равенство:
- Другими словами: логарифм, основанием которого является степень числа а равен произведению единицы делённой на показатель степени и логарифма числа b по основанию а.
- Эта теорема доказывается аналогично предыдущим, поэтому доказывать её мы не будем.
- Рассмотрим пример.
- Рассмотрим ещё один пример.
То есть нам удалось логарифм достаточно громоздкого выражения представить в виде суммы и разности логарифмов простых выражений. Такое преобразование называют логарифмированием.
Иногда приходиться решать обратную задачу: находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое действие называется потенцированием.
При этом используют следующее утверждение:
- Теорема 4.
- Равенство:
- справедливо тогда и только тогда, когда
- Это утверждение следует из монотонности логарифмической функции.
- Рассмотрим пример.
Ещё раз обратите внимание, что все свойства логарифмов мы получили при условии, что переменные принимают положительные значения. А как быть, если про знак переменной ничего неизвестно?
- Например, можно ли записать:
- Нет, нельзя, поскольку:
- Правильнее будет записать так:
- Мы должны помнить и о том, что:
- только в том случае, когда b > 0 и с > 0. Если мы в этом не уверены, но знаем, что произведение bc > 0, то, поскольку в этом случае выполняется равенство:
- то следует использовать формулу:
- Рассмотрим ещё несколько примеров.
- Пример.
- Пример.
- Пример.
- Пример.
- Итак, повторим основные свойства логарифмов:
Источник: https://videouroki.net/video/12-svoistva-logharifmov.html
Логарифм — свойства, формулы, график

Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Содержание
Определение логарифма ⇓Графики логарифма ⇓Свойства логарифма ⇓ Область определения, множество значений, возрастание, убывание ⇓ Частные значения ⇓ Основные формулы логарифмов ⇓ Основное свойство логарифмов и его следствия ⇓ Формула замены основания ⇓ Доказательство основных формул логарифмов ⇓Обратная функция ⇓Производная логарифма ⇓Интеграл ⇓Выражения через комплексные числа ⇓Разложение в степенной ряд ⇓
См. также:
Показательная функция, ее график, свойства, формулы Натуральный логарифм, функция ln x
Логарифм с основанием a – это функция y(x) = loga x, обратная к показательной функции с основанием a: x(y) = a y.
В дальнейшем будем считать, что основание логарифма a положительное, не равное единице число: .
Десятичный логарифм – это логарифм по основанию числа 10: lg x ≡ log10 x. Натуральный логарифм – это логарифм по основанию числа e: ln x ≡ loge x.
2,718281828459045…; .
Графики логарифма
 Графики логарифма y = loga x при различных значениях основания a.
Графики логарифма y = loga x при различных значениях основания a.
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
Свойства логарифма
См. также «Определение и доказательство свойств логарифма».
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 < x < + ∞ | 0 < x < + ∞ |
| Область значений | – ∞ < y < + ∞ | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | – ∞ | |
| – ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так: Логарифм по основанию e называется натуральным логарифмом:
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Логарифмирование – это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование – это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование.
При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
- Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
- Рассмотрим свойство показательной функции . Тогда
- .
- :
Применим свойство показательной функции .
Докажем формулу замены основания. ; . Полагая c = b, имеем:
Обратная функция
- Обратной для логарифма по основанию a является показательная функция с показателем степени a.
- Если , то
- Если , то
Производная логарифма
Производная логарифма от модуля x: . Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e. ; .
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям: . Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z: . Выразим комплексное число z через модуль r и аргумент φ: . Тогда, используя свойства логарифма, имеем:
.
Или Однако, аргумент φ определен не однозначно. Если положить , где n — целое, то будет одним и тем же числом при различных n.
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература: И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Источник: https://1cov-edu.ru/mat_analiz/funktsii/logarifm/
Изучение логарифмов в старшей школе
При решении показательных уравнений удается представить обе части уравнения в виде степеней с одинаковыми основаниями и рациональными показателями. Так, например, при решении уравнения мы заменяем степенью и из равенства степеней с одинаковыми основаниями делаем вывод о равенстве показателей: х = −5/6. Однако, чтобы решить, казалось бы, более простое уравнение 2х = 3, стандартных знаний оказывается недостаточно. Дело в том, что число 3 нельзя представить в виде степени с основанием 2 и рациональным показателем.
Действительно, если бы равенство , где m и n — натуральные числа, было верным, то, возведя его в степень n, мы должны были бы получить верное равенство 2m = 3n. Но последнее равенство неверно, так как левая его часть является четным числом, а правая — нечетным. Значит, не может быть верным и равенство .

С другой стороны, график непрерывной функции y = 2xпересекается с прямой y = 3, и, значит, уравнение 2x = 3 имеет корень. Таким образом, перед нами стоят два вопроса: «Как записать этот корень?» и «Как его вычислить?».
- Показатель степени, в которую нужно возвести число a (a > 0, a ≠ 1), чтобы получить число b, называется логарифмом b по основанию a и обозначается logab.
- Теперь мы можем записать корень уравнения 2х = 3:
- х = loga3
Равенства ax = b и x = logab, в которых число a положительно и не равно единице, число b положительно, а число x может быть любым, выражают одно и то же соотношение между числами a, b и x. Подставив в первое равенство выражение x из второго, получим основное логарифмическое тождество.
Понятие логарифма в методическом пособии
Задание
Решите уравнение: а) 2x = 64; б) ; в) ; г) 4x = 0; д) 7x = −12.
После проверки ученикам предлагается ответить на вопрос, какое из заданий показалось им наиболее трудным. Вероятный ответ: 2 (в), так как в нем нужно было приводить дробь к степени числа 5.
Затем школьникам предлагается высказать мнение о сравнительной с заданием 2 (в) трудности уравнения 2x = 3.
На первый взгляд кажется, что это уравнение проще, однако представить 3 в виде степени числа 2 школьникам не удается.
Дальше изучение нового материала проводится в соответствии с учебником. При этом в зависимости от уровня класса рассматривается или не рассматривается дополнительный материал о невозможности представления 3 в виде 2r , где r = m/n.
После этого диалог с классом можно строить примерно так:
— Как вы думаете, имеет ли уравнение 2x = 3 корень? Ответ обоснуйте. [Если построить график функции у = 2x и провести прямую у = 3, то они пересекутся в одной точке, значит, уравнение имеет один корень.] — Что можно сказать о корне уравнения ax = b, где а > 0 и а ≠ 1? При всех ли значениях b оно имеет корни?
Затем вводится определение логарифма числа b по основанию а и записывается основное логарифмическое тождество .
При этом выписывание равенства происходит синхронно с повторным чтением определения теперь уже в обратном, по сравнению с учебником, порядке.
Теперь можно записать корень уравнения 2х = 3: х = loga3 и предложить школьникам серию самостоятельных работ.
Логарифмическая функция
Выразим x из равенства y = logax, получим x = ay. Последнее равенство задает функцию x = ay, график которой симметричен графику показательной функции y = ax относительно прямой y = x.
Показательная функция x = ay является монотонной, и, значит, разные значения y соответствуют разным значениям x, но это говорит о том, что y = logax, в свою очередь, является функцией x.
Показательная функция y = ax и логарифмическая функция y = logax являются взаимно обратными. Сравнивая их графики, можно отметить некоторые основные свойства логарифмической функции.
Свойства функции y = logax, a > 0, a ≠ 11:
- Функция y = logax определена и непрерывна на множестве положительных чисел.
- Область значений функции y = logax — множество действительных чисел.
- При 0 < a < 1 функция y = logax является убывающей; при a > 1 функция y = logax является возрастающей.
- График функции y = logax проходит через точку (1; 0).
- Ось ординат — вертикальная асимптота графика функции y = loga.
Решение логарифмических уравнений и неравенств на основе свойств логарифмической функции
Освобождаясь от внешнего логарифма, имеющего основание 3, мы ссылаемся на возрастание соответствующей логарифмической функции, то есть на то, что большему значению логарифма соответствует большее значение выражения, стоящего под его знаком.
Однако следует иметь в виду, что если функцию y = log3 log0,5(2x + 1) считать логарифмической, то ее аргумент не переменная x, а все выражение log0,5(2x + 1).
Если же все-таки рассматривать x как аргумент функции y = log3 log0,5(2x + 1), то эта функция окажется убывающей, так как при увеличении значения x увеличивается значение выражения 2x + 1, уменьшается значение выражения log0,5(2x + 1) и, соответственно, уменьшается значение самой функции.
Свойства логарифмов
Связь двух форм записи соотношения между числами a, b и x (речь о ax = b и x = logab) позволяет получить свойства логарифмов, основываясь на известных свойствах степеней.
Рассмотрим, например, произведение степеней с одинаковым основанием: axay. Пусть a x = b и a y = c.
Перейдем к логарифмической форме: x = logab и y = logac, тогда bc = a logab × a logac = a logab +logac.
От показательной формы равенства bc = a logab +logac перейдем к логарифмической форме:
- loga(bc) = logab + logac
- Заметим, что в левой части формулы числа a и b могут быть отрицательными. Тогда формула будет выглядеть так:
- loga(bc) = loga|b| + loga|c|
- Аналогично можно получить еще два свойства для логарифмов частного и степени.
- логарифм произведения loga (bc) = loga |b| + loga |c|
- логарифм частного
- логарифм степени logabp = p loga|b|
Последнее свойство дает возможность вывести важную формулу, с помощью которой можно выразить логарифм с одним основанием через логарифм с другим основанием.
Пусть logab = x. Перейдем к показательной форме ax = b. Прологарифмируем это равенство по основанию c, т.е.
найдем логарифмы с основанием c обеих частей этого равенства: logcax = logcb.
Применяя к левой части свойство логарифма степени, получим x logca = logcb или , откуда .
- Формула перехода от одного основания логарифма к другому
- Полезно запомнить частный случай формулы перехода, когда одно из оснований является степенью другого:
- Рассмотренные свойства и формула перехода «работают», конечно, только когда все входящие в них выражения имеют смысл.
Логарифмы на ЕГЭ
Логарифмы встречаются на ЕГЭ: как во второй части (обычно, это задание 15), так и, реже, в первой части. Задания из аттестации — одно из средств мотивации детей на уроках. Зная, что упражнение на доске аналогично заданию ЕГЭ, ученик будет внимательнее следить за его решением.
Разберем несколько таких заданий.
Из первой части (определение логарифма на ЕГЭ профильного уровня)
Решите уравнение log3(x+1)2 + log3|x+1| = 6 . Если корней несколько, укажите наименьший из них.
Решение. Решаем квадратное относительно log3|x+1| уравнение. Его корни 2 и −3.
log3|x+1| = 2, |x+1| = 9, x = −10 — это наименьший из корней.
Ответ: −10.
Из второй части (логарифмическое неравенство на ЕГЭ профильного уровня)
Решите неравенство .
Решение. ОДЗ: x > 0, x ≠ 1. Перейдем к логарифмам по основанию 10:
- ;
- ;
- Умножим числитель и знаменатель на 2, чтобы уйти от радикала:
- ;
- Нули числителя: 2/3, 3, с учетом положительности x, нуль заменяется на 1.
- Ответ:
Алгебра в таблицах. 7-11 классы. Справочное пособие
Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики и примеры решения типовых задач. В конце книги помещен предметный указатель. Пособие будет полезно учащимся 7-11 классов, абитуриентам, студентам, учителям и родителям.
Купить
Из второй части (логарифмическое уравнение с параметром на ЕГЭ профильного уровня)
- Найдите все значения a, для которых при любом положительном значении b уравнение имеет хотя бы одно решение, меньше 1/3.
- Решение. Найдем ОДЗ:
- Стандартно приводим логарифмы к одному основанию
- ,
- .
- Получили квадратное уравнение относительно .
- Оно должно иметь корень при
- Обозначим, что и рассмотрим квадратичную функцию y = t2 — bt — 2a.
Ветви ее графика направлены вверх, а вершина, поскольку b > 0, расположена в левой координатной полуплоскости.
Первая ветвь параболы пересекает ось абсцисс правее t = 0, значит при t = 0 y < 0. Получаем −2a < 0 a > 0.
Ответ: a > 0.
Учебник «Алгебра и начала математического анализа. Углубленный уровень. 10 класс» схож по структуре с учебником базового уровня, однако предполагает больше часов на изучение сложных задач.
Эти и другие издания линейки вы можете апробировать прямо сейчас, воспользовавшись акцией «5 учебников бесплатно». Методическое пособие представлено в свободном доступе.
Приглашаем познакомиться с другими вебинарами экспертов и порекомендовать нам интересующую вас тему для последующих трансляций.
#ADVERTISING_INSERT#
Источник: https://rosuchebnik.ru/material/izuchenie-logarifmov-v-starshey-shkole-article/
math4school.ru
Формулы перехода от десятичного к натуральному логарифму и наоборот
Определение логарифма
- Логарифмом положительного числа b по основанию а (a > 0, a ≠ 1) называется такой показатель степени c, в которую нужно возвести число а, чтобы получить число b.
- Записывают: с = loga b, что означает a c = b.
- Из определения логарифма следует справедливость равенства:
- a loga b = b, (а > 0, b > 0, a ≠ 1),
- называемого основным логарифмическим тождеством.
- В записи loga b число а – основание логарифма, b – логарифмируемое число.
- Из определения логарифмов вытекают следующие важные равенства:
- loga 1 = 0,
- loga а = 1.
- Первое следует из того, что a 0 = 1, а второе – из того, что a 1 = а. Вообще имеет место равенство
- loga a r = r.
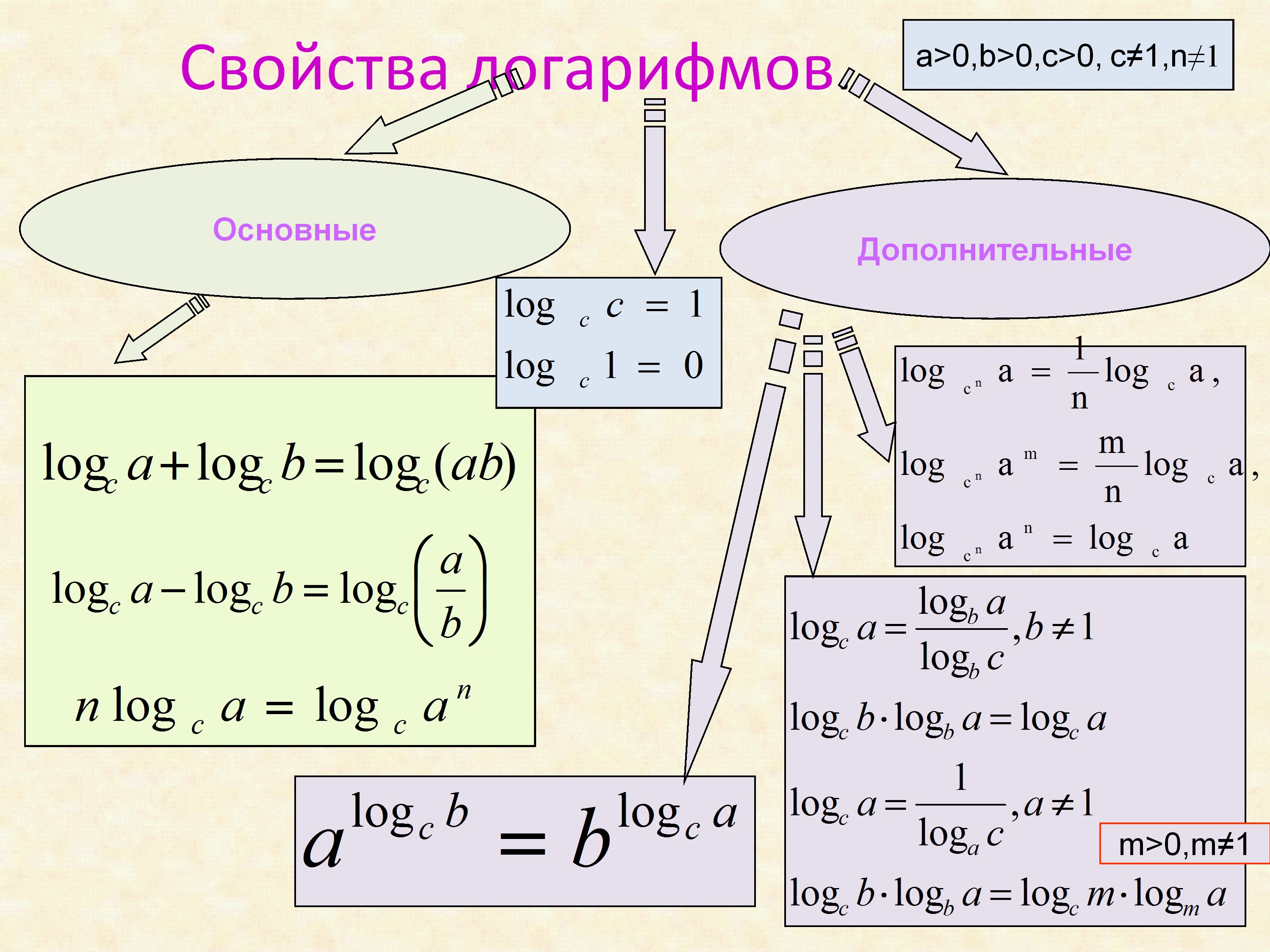
Свойства логарифмов
- Для положительных действительных чисел a (a ≠ 1), b, c справедливы следующие соотношения:
- loga (b · c) = loga b + loga c
- loga (b ⁄ c) = loga b – loga c
- loga b p = p · loga b
- loga q b = 1/q · loga b
- loga q b p = p/q · loga b
- loga pr b ps = loga r b s
- loga b = logc b ⁄ logc a (c ≠ 1)
- loga b = 1 ⁄ logb a (b ≠ 1)
- loga b · logb c = loga c
- c loga b = b loga c
- Замечание 1. Если а > 0, a ≠ 1, числа b и c отличны от 0 и имеют одинаковые знаки, то
- loga (b · c) = loga |b| + loga |c|
- loga (b ⁄ c) = loga |b| – loga |c| .
- Замечание 2. Если p и q – чётные числа, а > 0, a ≠ 1 и b ≠ 0, то
- loga b p = p · loga |b|
- loga pr b ps = loga r |b s|
- loga q b p = p/q · loga |b| .
- Для любых положительных, отличных от 1 чисел a и b верно:
- loga b > 0 тогда и только тогда, когда a > 1 и b > 1 или 0 < a < 1 и 0 < b < 1;
- loga b < 0 тогда и только тогда, когда a > 0 и 0 < b < 1 или 0 < a < 1 и b > 1.
Десятичный логарифм
- Десятичным логарифмом называется логарифм, основание которого равно 10.
- Обозначаются символом lg:
- log10 b = lg b.
Десятичные логарифмы до изобретения в 70-х годах прошлого века компактных электронных калькуляторов широко применялись для вычислений.
Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня.
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже – с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми.
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log, Log, Log10, причём следует иметь в виду, что первые два варианта могут относиться и к натуральному логарифму.
Таблица десятичных логарифмов целых чисел от 0 до 99
| Десятки | Единицы | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| – | 0,30103 | 0,47712 | 0,60206 | 0,69897 | 0,77815 | 0,84510 | 0,90309 | 0,95424 | ||
| 1 | 1 | 1,04139 | 1,07918 | 1,11394 | 1,14613 | 1,17609 | 1,20412 | 1,23045 | 1,25527 | 1,27875 |
| 2 | 1,30103 | 1,32222 | 1,34242 | 1,36173 | 1,38021 | 1,39794 | 1,41497 | 1,43136 | 1,44716 | 1,46240 |
| 3 | 1,47712 | 1,49136 | 1,50515 | 1,51851 | 1,53148 | 1,54407 | 1,55630 | 1,56820 | 1,57978 | 1,59106 |
| 4 | 1,60206 | 1,61278 | 1,62325 | 1,63347 | 1,64345 | 1,65321 | 1,66276 | 1,67210 | 1,68124 | 1,69020 |
| 5 | 1,69897 | 1,70757 | 1,71600 | 1,72428 | 1,73239 | 1,74036 | 1,74819 | 1,75587 | 1,76343 | 1,77085 |
| 6 | 1,77815 | 1,78533 | 1,79239 | 1,79934 | 1,80618 | 1,81291 | 1,81954 | 1,82607 | 1,83251 | 1,83885 |
| 7 | 1,84510 | 1,85126 | 1,85733 | 1,86332 | 1,86923 | 1,87506 | 1,88081 | 1,88649 | 1,89209 | 1,89763 |
| 8 | 1,90309 | 1,90849 | 1,91381 | 1,91908 | 1,92428 | 1,92942 | 1,93450 | 1,93952 | 1,94448 | 1,94939 |
| 9 | 1,95424 | 1,95904 | 1,96379 | 1,96848 | 1,97313 | 1,97772 | 1,98227 | 1,98677 | 1,99123 | 1,99564 |
Натуральный логарифм
- Натуральным логарифмом называется логарифм, основание которого равно числу е, математической константе, являющейся иррациональным числом, к которому стремится последовательность
- аn = (1 + 1/n)n при n → +∞.
- Иногда число e называют числом Эйлера или числом Непера. Значение числа е с первыми пятнадцатью цифрами после запятой следующее:
е = 2,718281828459045… .
- Натуральный логарифм обозначаются символом ln:
- loge b = ln b.
- Натуральные логарифмы являются самыми удобными при проведении различного рода операций, связанных с анализом функций.
Таблица натуральных логарифмов целых чисел от 0 до 99
| Десятки | Единицы | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| – | 0,69315 | 1,09861 | 1,38629 | 1,60944 | 1,79176 | 1,94591 | 2,07944 | 2,19722 | ||
| 1 | 2,30259 | 2,39790 | 2,48491 | 2,56495 | 2,63906 | 2,70805 | 2,77259 | 2,83321 | 2,89037 | 2,94444 |
| 2 | 2,99573 | 3,04452 | 3,09104 | 3,13549 | 3,17805 | 3,21888 | 3,25810 | 3,29584 | 3,33220 | 3,36730 |
| 3 | 3,40120 | 3,43399 | 3,46574 | 3,49651 | 3,52636 | 3,55535 | 3,58352 | 3,61092 | 3,63759 | 3,66356 |
| 4 | 3,68888 | 3,71357 | 3,73767 | 3,76120 | 3,78419 | 3,80666 | 3,82864 | 3,85015 | 3,87120 | 3,89182 |
| 5 | 3,91202 | 3,93183 | 3,95124 | 3,97029 | 3,98898 | 4,00733 | 4,02535 | 4,04305 | 4,06044 | 4,07754 |
| 6 | 4,09434 | 4,11087 | 4,12713 | 4,14313 | 4,15888 | 4,17439 | 4,18965 | 4,20469 | 4,21951 | 4,23411 |
| 7 | 4,24850 | 4,26268 | 4,27667 | 4,29046 | 4,30407 | 4,31749 | 4,33073 | 4,34381 | 4,35671 | 4,36945 |
| 8 | 4,38203 | 4,39445 | 4,40672 | 4,41884 | 4,43082 | 4,44265 | 4,45435 | 4,46591 | 4,47734 | 4,48864 |
| 9 | 4,49981 | 4,51086 | 4,52179 | 4,5326 | 4,54329 | 4,55388 | 4,56435 | 4,57471 | 4,58497 | 4,59512 |
Формулы перехода от десятичного к натуральному логарифму и наоборот
Так как lg е = 1 / ln 10 ≈ 0,4343, то lg b ≈ 0,4343 · ln b;
так как ln 10 = 1 / lg e ≈ 2,3026, то ln b ≈ 2,3026 · lg b.
Источник: http://math4school.ru/logarifm.html




