Формулы периметра параллелограмма

Общие сведения о фигуре

Параллелограмм — это четырехугольник на плоскости, у которого присутствует равенство противоположных сторон, причем они лежат на параллельных прямых.

Ромб, прямоугольник и квадрат — его частные случаи. Из него состоят более сложные объемные фигуры. Например, параллелепипед и куб.

Высота параллелограмма — отрезок, который является перпендикуляром, проведенным к нижней стороне геометрической фигуры.

Всего можно провести четыре высоты. Две из них можно провести из вершин углов, которые лежат в параллелограмме и являются тупыми. Другие две высоты проводятся из острых углов (находятся вне фигуры). Углы делятся на шесть типов: острые, прямые, тупые, развернутые, выпуклые и полные.

Первый тип, градусная размерность которого меньше 90, является острым. Если значение равно 90, то он является прямым, и соответствует второму типу.

В случае, когда выполняется условие 90 < a < 180, то угол считается тупым. При равенстве a = 180 — развернутый. При неравенстве 180 < a < 360 — выпуклый (смежный с ним угол является острым).

Полным называется угол, градусная мера которого соответствует 360.

Для решения задач и выполнения расчетов необходимо знать следующие аспекты: свойства и признаки параллелограмма, а также уметь находить его углы, стороны, диагонали, периметр и площадь. Кроме того, следует знать не только основные соотношения фигуры, которая вписана в окружность, но и в случае, когда окружность находится внутри нее.

Информация о признаках

Признаки позволяют выяснить принадлежность фигуры к параллелограмму. Например, существует произвольный четырехугольник, и нужно выяснить, является ли он параллелограммом. Необходимо отметить, что при условии совпадения хотя бы одного из признаков, этот четырехугольник является им. Проверку следует производить, руководствуясь следующими утверждениями:

• Параллельность и равенство двух любых сторон.
• Равенство противолежащих сторон.
• Углы, которые являются противолежащими, равны.
• Точка пересечения диагоналей (центр симметрии) делит их на два равных отрезка.
• При выполнении равенства (d — диагонали): (d1)^2 + (d2)^2 = a 2 + b 2 + c 2 + d 2 .

Последний признак можно записать для упрощения расчетов следующим образом: sqr (d1) + sqr (d2) = 2 * (a 2 + b 2 ). Равенство можно упростить, поскольку противоположные стороны равны.

Основные свойства

Для решения задач и проектирования деталей необходимо знать основные свойства параллелограмма. Некоторые из них были получены при доказательстве и следствиях из теорем. К ним относятся следующие:

• Ромб, квадрат и прямоугольник — параллелограммы.
• Противоположные стороны одинаково равны и параллельны.
• Противолежащие углы равны.
• Суммарное значение градусной меры всех внутренних углов параллелограмма составляет 360.
• Сумма углов, прилегающих к одной из вершин, составляет 180 градусов.
• Диагональ делит фигуру на два треугольника, которые равны между собой по всем признакам.
• Две диагонали (одна — большая, а другая — меньшая) делят параллелограмм на две пары треугольников, которые равны между собой.
• Диагонали фигуры пересекаются, а точка пересечения делит их пополам (через нее можно провести среднюю линию, которая параллельна сторонам).
• Точка пересечения двух диагоналей является симметрией фигуры.
• Биссектрисы соседних углов пересекаются под углом в 90 градусов, а противоположных являются параллельными.
• sqr (d1) + sqr (d2) = 2 * ((a)^2 + (b)^2).

Однако для выполнения расчетов признаков и свойств параллелограмма недостаточно. В некоторых случаях требуется вычислить периметр и площадь фигуры. Соотношения используются не только в учебных заведениях, но и в научных исследованиях. Простым примером является нахождение площади поперечного сечения проводника. Это может понадобиться для дальнейшего вычисления электрического сопротивления.

Определение периметра

Периметром (P) любой фигуры является сумма длин всех ее сторон. Следовательно, для параллелограмма найти это значение является несложным. Базовая формула периметра параллелограмма имеет следующий вид: P = a + b + c + d = 2 * (a + b). Кроме того, существуют и другие соотношения для нахождения этой величины:

1. Если известны одна из сторон и две диагонали.
2. Нахождение периметра через сторону, высоту и синус угла.

В первом случае соотношение для стороны «a» записывается следующим образом: P = 2 * a + sqrt [2 * (d1 * d1 + d2 * d2 — 2 * a^(2))]. Для «b» запись изменяется таким образом: P = 2*b + sqrt [2 * (d1^(2) + d2^(2) — 2 * b^(2))].

Во втором случае, когда известна сторона «а», угол BAD и высота Ha, периметр записывается формулой вида: P = 2 * [a + Ha / sin (BAD)]. Для стороны «b», угла BAD и высоты Hb равенство принимает следующий вид: P = 2 * [b + Hb / sin (BAD)]. Если проанализировать последние два соотношения, то величины «Hb / sin (BAD)» и «Hа / sin (BAD)» являются стороной «b» и «a» соответственно.

Вычисление площади

Площадь параллелограмма (S) — это пространство, которое ограничено его сторонами, и равно произведению одной из сторон на высоту, проведенную к одноименному основанию. Базовая формула нахождения значения S является следующей: S = a * Ha = b * Hb. Кроме того, существует два способа нахождения ее значения, когда известны следующие величины:

1. По сторонам и углу.
2. Две диагонали и синус углов f или g между ними.

Можно записать соотношение следующим образом: S = a * b * sin (BAD) = a * b * sin (ABC). В последнем случае математическая запись площади имеет следующий вид: S = 0,5 * d1 * d2 * sin (f) = 0,5 * d1 * d2 * sin (g).

Кроме того, существует формула Герона, которая позволяет вычислить площадь параллелограмма. Для этого необходимо вычислить полупериметр (p) треугольника со сторонами a, b и d: p = P / 2 = (a + b + d).

Формула имеет вид: S = sqrt[p * (p — a) * (p — b) * (p — d)].

Соотношения сторон и диагоналей

В некоторых задачах необходимо определить неизвестные длины сторон или диагонали. Можно попытаться вывести соотношения, однако эта процедура занимает некоторое время. Следовательно, проще воспользоваться уже готовыми формулами. Стороны параллелограмма можно определить четырьмя основными выражениями. При этом следует знать следующие величины:

1. Диагонали и угол.
2. Другую сторону и диагонали.
3. Высоту и значение синуса угла в градусах.
4. Площадь и высоту.

В первом случае для вычисления длины стороны «а», следует воспользоваться следующей формулой: a = [sqrt (d1 *d1 + d2 * d2 — 2 * d1 * d2 * cos (f))] / 2 = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (g))] / 2. Значение стороны «b» вычисляется немного иначе: b = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (f))] / 2 = [sqrt (sqr (d1) + sqr (d2) — 2 * d1 * d2 * cos (g))] / 2.

При известных значениях диагоналей и одной из сторон, соотношение имеет более простой вид, чем в первом случае: a = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * b 2 ))] / 2 и b = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * a 2 ))] / 2.

Диагональ параллелограмма — отрезок, который соединяет его противоположные внутренние углы. Фигура имеет две диагонали, одна из которых длинная (d1), а другая является короткой (d2). Их можно найти, используя 4 соотношения. Это возможно в том случае, когда известны следующие данные:

• Стороны и косинус угла ABC.
• Cos (BAD) и стороны.
• Одну известную диагональ и стороны.
• Площадь, диагональ и угол между d1 и d2.

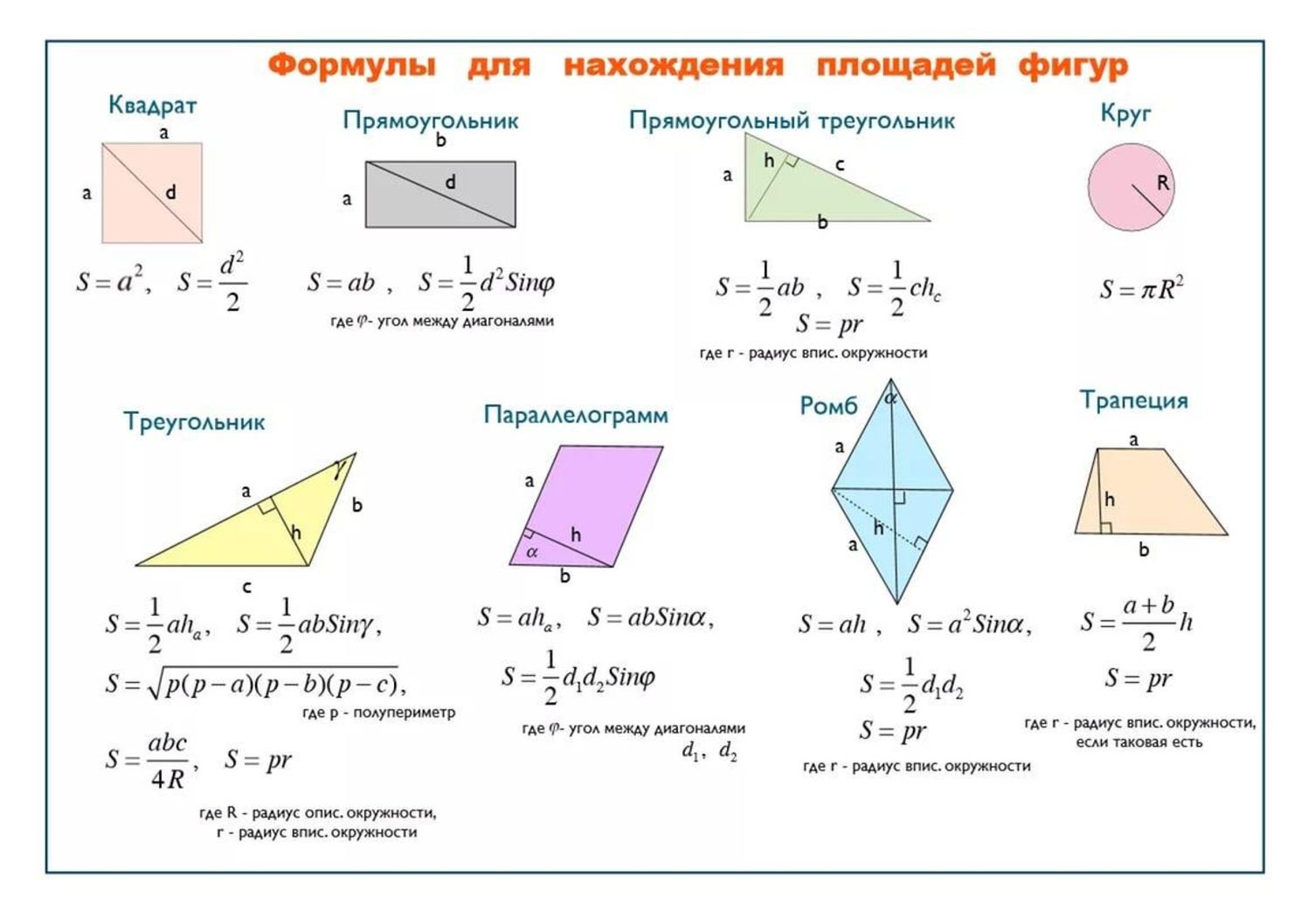
В первом случае можно воспользоваться следующими формулами (теорема косинусов): d1 = sqrt[a 2 + b 2 — 2 * a * b * cos (ABC)] и d2 = sqrt[a 2 + b 2 + 2 * a * b * cos (ABC)]. Во втором: d1 = sqrt[a 2 + b 2 + 2 * a * b * cos (BAD)] и d2 = sqrt[a 2 + b 2 — 2 * a * b * cos (BAD)].

Когда известны две стороны и одна из диагоналей, то можно воспользоваться третьим случаем: d1 = sqrt[2 * a 2 + 2 * b 2 — (d2)^2] и d2 = sqrt[2 * a 2 + 2 * b 2 — (d1)^2]. В последнем случае равенства для нахождения диагоналей имеют такой вид: d1 = 2 * S / [(d2) * sin (f)] = 2 * S / [(d2) * sin (g)] и d2 = 2 * S / [(d1) * sin (f)] = 2 * S / [(d1) * sin (g)].

Параллелограмм и окружность

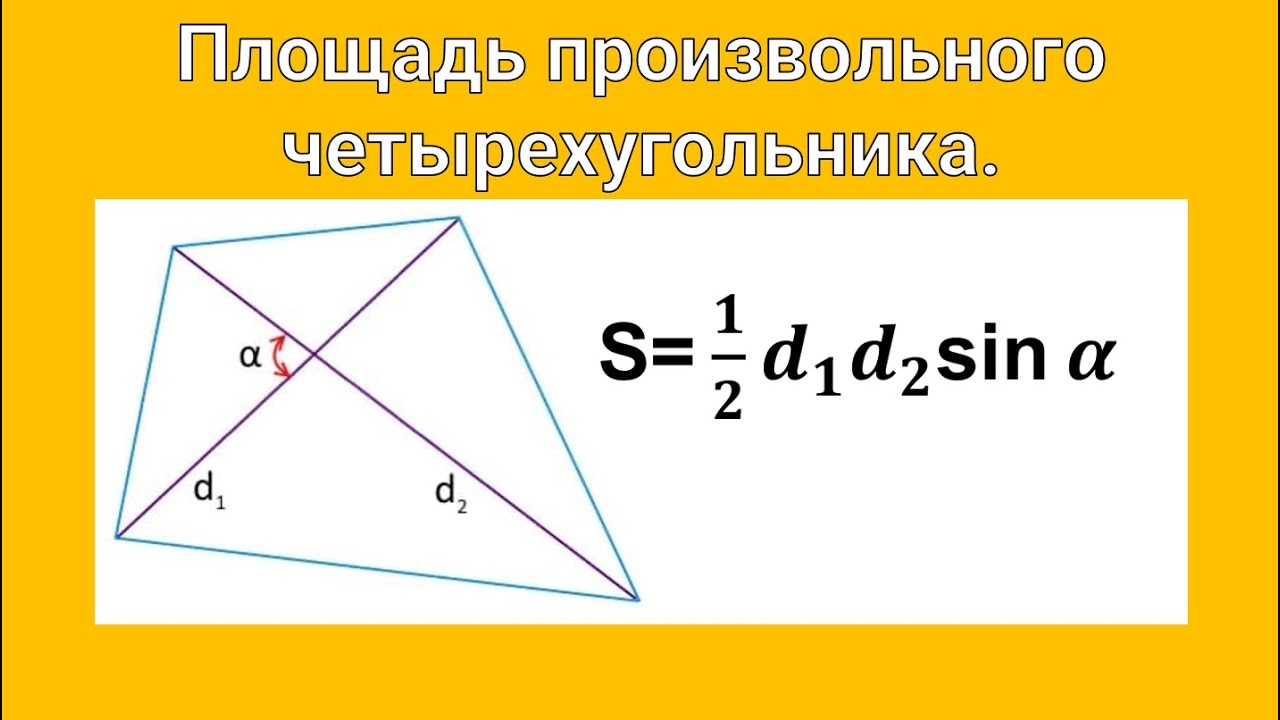
Существуют определенный тип задач, в которых речь идет о параллелограмме и окружности. Всего бывает два варианта: вписанная и описанная окружности. Следует отметить, что не всегда это возможно. Существуют определенные условия, при которых возможны такие операции. Кроме того, следует обратить особое внимание на дополнительные свойства, которые появляются при комбинации данных фигур. Можно не только чередовать комбинации, но и использовать одновременно.

Для решения сложного типа задач и выполнения расчетов, в некоторых случаях рекомендуется применять вписанные и описанные окружности. Например, при проектировании деталей, необходимо полностью подогнать ее размеры, поскольку они должны быть правильной формы. При помощи окружности (вписанной или описанной) можно выявить ряд дефектов, которые могут привести к некорректной работе механизма.

Круг и прямоугольник

Главное условие: любой четырехугольник можно вписать в окружность, когда сумма его двух противоположных углов составляет 180 градусов. У параллелограмма есть одно свойство: сумма углов, которые прилегают к любой из вершин, составляет 180 градусов. Кроме того, сумма всех его углов составляет 360, а, следовательно, сумму противоположных углов составляет 360 — 180 = 180 (градусов).

Однако при попытке описать около него окружность ничего не выйдет, поскольку есть одно свойство: противоположные углы у него равны. Ими могут быть тупые и острые. Сумма градусной меры тупых углов будет больше 180, а острых — меньше.

Когда противоположные углы будут равны 90, то значит их сумма составит 180. В этом случае нужно рассматривать частный случай — прямоугольник.

Появляется очень важное свойство: диагонали прямоугольника пересекаются и точкой пересечения (центром окружности) делятся пополам, а также являются диаметрами окружности.

Для нахождения радиуса окружности, следует воспользоваться следующим соотношением (при условии, что известны стороны прямоугольника): R = [sqrt (a 2 + b 2 )] / 2 = d / 2. Величина «d» является диаметром.

Ромб и квадрат

В параллелограмм также можно вписать окружность. Однако для этого необходимо выполнение определенного условия. Оно заключается в следующем: суммы противолежащих сторон параллелограмма должны быть равны. Нужно отметить, что это выполняется только для ромба и квадрата.

Ромбом называется параллелограмм, стороны которого равны, а углы не равны 90 градусов. Квадрат — геометрическая фигура, у которой все стороны и углы равны. Из последнего определения можно найти значение градусной меры одного угла: 360 / 4 = 90.

Последняя фигура является частным случаем ромба. Радиус окружности находится с помощью формулы: r = S / p = 0,5 * H. В этом соотношении переменные S, p и H — площадь, полупериметр и высота соответственно.

Для нахождения S можно воспользоваться такими соотношениями:

• Известны длина стороны (а) и высота (H): S = a * H.
• Через диагонали d1 и d2: S = d1 * d2 / 2.

Полупериметром фигуры называется половина от значения ее периметра. Соотношение записывается таким образом: p = P / 2 = 4 * a.

Таким образом, знать основные свойства и признаки параллелограмма необходимо, поскольку от этого может зависеть не только качество сдачи экзаменов, решения задач, но и проектирование различных деталей.

Источник: https://nauka.club/matematika/parallelogramm-ego-svoystva.html

площа па

Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.

Свойства параллелограмма

Противоположные стороны параллелограмма как и противоположные углы равны между собой: AB=CD, BC=AD,

• Диагонали параллелограмма в точке пересечения делятся на две равные части:
• АО=OC, OB=OD.
• Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.
• 
• Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.

Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:

AC^2+BD^2=2*(AB^2+BC^2).

Основные признаки параллелограммов:

1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом. 2. Четырехугольник с равными противоположными сторонами является параллелограммом. 3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом. 4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.

5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом

Биссектрисы параллелограмма

Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.

Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).

Высота параллелограмма

Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.

Формула площади параллелограмма

1. Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
2. Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
3. На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.

Периметр параллелограмма

Формула для вычисления периметру параллелограмма имеет вид то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.

Посмотреть материалы:

Источник: https://yukhym.com/ru/geometriya/perimetr-ploshchad-parallelogramma.html

Формулы параллелограмма

Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.

1. Противоположные стороны параллельны и равны.
2. Противоположные углы равны
3. Точка пересечения диагоналей делит их пополам.
4. Сумма углов четырехугольника прилегающих к любой стороне равна 180°
5. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
6. Сумма углов параллелограмма равна 360°
7. Каждая диагональ делит параллелограмма на два равных треугольника
8. Биссектрисы противоположных углов параллелограмма всегда параллельны
9. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)

Длины сторон через диагонали и угол между ними

$$ AB = {1 over 2} * sqrt{AC^2 + BD^2 — 2 * AC * BD * cos(α)} $$ $$ AB = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(β)} $$ $$ BC = {1 over 2} * sqrt{AC^2 + BD^2 — 2 * AC * BD * cos(β)} $$ $$ BC = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(α)} $$

Длина стороны через диагонали и известную сторону

$$ AB = sqrt{AC^2 + BD^2 — 2 * BC^2 over 2} $$ $$ BC = sqrt{AC^2 + BD^2 — 2 * AB^2 over 2} $$

Длины сторон через высоты и угол между сторонами

$$ AB = {BH_{AD} over sin(α)} = {BH_{AD} over sin(β)} $$ $$ BC = {BH_{DC} over sin(α)} = {BH_{DC} over sin(β)} $$

Длина диагонали через стороны и углы между ними

$$ AC = sqrt{AB^2 + BC^2 — 2 * AB * BC * cos(β)} $$ $$ AC = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(α)} $$ $$ BD = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(β)} $$ $$ BD = sqrt{AB^2 + BC^2 — 2 * AB * BC * cos(α)} $$

Длина диагонали через стороны и известную диагональ

$$ AC = sqrt{2 * AB^2 + 2 * BC^2 — BD^2} $$ $$ BD = sqrt{2 * AB^2 + 2 * BC^2 — AC^2} $$

Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями

$$ AC = {2 * S over BD * sin(α)} = {2 * S over BD * sin(β)} $$ $$ BD = {2 * S over AC * sin(α)} = {2 * S over AC * sin(β)} $$

• Косинус острого угла
• Косинус тупого угла
• Синус острого и тупого угла через площадь и стороны параллелограмма

$$ cos(α) = {AB^2 + BC^2 — BD^2 over 2 * AB * BC} $$ $$ cos(β) = {AB^2 + BC^2 — AC^2 over 2 * AB * BC} $$ $$ sin(α) = sin(β) = {S over AB * BC} $$

1. Косинус острого угла через стороны и диагонали
2. Косинус тупого угла через стороны и диагонали
3. Синус острого и тупого угла через площадь и диагонали

$$ cos(α) = {AC^2 + BD^2 — 4 * AB^2 over 2 * AC * BD} $$ $$ cos(α) = {BC^2 — AB^2 over AC * BD} $$ $$ cos(β) = {AC^2 + BD^2 — 4 * BC^2 over 2 * AC * BD} $$ $$ cos(β) = {AB^2 — BC^2 over AC * BD} $$ $$ sin(α) = sin(β) = {2 * S over AC * BD} $$

$$ BH_{AD} = AB * sin(α) = AB * sin(β) $$ $$ BH_{DC} = BC * sin(α) = BC * sin(β) $$

$$ AA_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 — 2 * cos(β)} $$ $$ AA_1 = 2 * AB * cos({α over 2}) $$ $$ DD_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 — 2 * cos(β)} $$ $$ DD_1 = 2 * AB * cos({α over 2}) $$

Источник: http://calc-online24.ru/formula/parallelogram

Периметр параллелограмма

Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.

Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.

• 
  У параллелограмма есть несколько основных признаков.

Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)

— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм. — Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.

— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.

— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.

1. Периметр параллелограмма находится по формуле

Р = 2 (а+b)

• что означает что периметр равняется двойной сумме сторон.
• Биссектриса параллелограмма

Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то: Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.

Так же они могут совпадать и быть параллельны друг другу.
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.

Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.

S = a * ha = b * hb

Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.

S = a * b * sin(?) = a * b * sin(?)

Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.

Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www.imperia.ru/client/temp_staff/) и узнайте подробнее.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источник: https://reshit.ru/perimetr-parallelogramma

Формула площади и периметра параллелограмма

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны. Частными вариантами параллелограмма являются ромб, прямоугольник и квадрат.

Любой параллелограмм характеризуется сторонами a и b и высотой h (см. рисунок). Также при решении задач может понадобиться угол α между сторонами параллелограмма. Именно эти характеристики используются в формулах параллелограмма при вычислении площади и периметра.

Формула периметра параллелограмма

Периметр P параллелограмма можно получить, зная его стороны:

Формулы площади параллелограмма

• Площадь параллелограмма S можно вычислить, зная его сторону и высоту h, проведенную к этой стороне:
• Также площадь параллелограмма S можно вычислить, зная его стороны и угол α между ними:
• Поделитесь статьей с одноклассниками «ПАРАЛЛЕЛОГРАММ формулы площади и периметра».

Параллелограмм – это четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Формула площади параллелограмма:

Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

1. S – площадь параллелограмма
2. a – длина основания
3. h – длина высоты

Формула периметра параллелограмма:

Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).

• P – периметр параллелограмма
• a – длина 1-ой стороны параллелограмма
• b – длина 2-ой стороны параллелограмма

Параллелограмм – это четырехугольник, противоположные стороны которого параллельны и не образуют прямой угол. Диагонали в точке пересечения делятся пополам, но они не равны и не перпендикулярны.

Высоты – это перпендикулярные расстояния между двумя противоположными сторонами, их длина определяется с помощью функции синуса прямоугольных треугольников, которые они совместно со сторонами параллелограмма образуют.

  Функция кнопки insert 7 букв сканворд

Формулы

• P – периметр
• S – площадь
• a,b – стороны

• d1,2 – диагонали
• h a – высота на сторону a
• h b – высота на сторону b

При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.

Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.

• Мария Сухоруких
• Распечатать

Источник: https://4apple.org/formula-ploshhadi-i-perimetra-parallelogramma/

Формула периметра параллелограмма

Параллелограмм это четырехугольник, у которого противоположные стороны попарно параллельны.

По свойству параллелограмма его противоположные стороны равны. Поэтому для нахождения периметра параллелограмма ABCD со сторонами AB = CD = a и AC = BD = b будет справедлива формула:

• Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.
• [ P_{ riangle ABCD} = a+b+a+b = 2cdot a+2cdot b=2cdot left (a+b
  ight) ]
• [ LARGE P_{ riangle ABCD} = 2cdot left (a+b
  ight) ]
• где: P — периметр параллелограмма a — длина малой стороны параллелограмма b — длина большой стороны параллелограмма

Формулы периметраРасчёт Площадь Математика Тригонометрия Формулы Теория

Найти периметр параллелограмма ABCD со сторонами a = 7.62 см и b = 9.33 см.

Для нахождения периметра параллелограмма воспользуемся формулой ( P_{ riangle ABCD} = 2cdot left (a+b
ight) )

Подставляя данные задачи в эту формулу, получим:

( P_{ riangle ABCD} = 2cdot left (7.62 + 9.33
ight) = 2 cdot 16.95 = 33.9 ) см

( P_{ riangle ABCD} = 33.9 ) см

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

• Формула периметра треугольникаПериметр треугольника равен сумме длин его сторон
• Формула периметра равнобедренного треугольникаПериметр равнобедренного треугольника равен сумме длин его сторон
• Формула периметра равностороннего треугольникаПериметр равностороннего треугольника равен тройной сумме длины его стороны
• Периметр круга радиуса r равен удвоенному произведению радиуса r на число пи (~3.1415)
• Формула периметра трапецииПериметр трапеции равен сумме длин всех четырех сторон
• Формула периметра прямоугольникаПериметр прямоугольника — это сумма длины и ширины, умноженная на «2».
• Формула периметра квадратаПериметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны)
• Периметр ромба равен сумме длин всех его сторон, или длинна стороны умноженная на 4

• Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
• Согласно нормам Всемирной Организацией Здравоохранения (ВОЗ)
• 1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
• 1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
• Сколько в ампере ватт, как перевести амперы в ватты и киловаттыМощность – это скорость расходования энергии, выраженная в отношении энергии ко времени: 1 Вт = 1 Дж/1 с. Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.

Источник: https://calcsbox.com/post/formula-perimetra-parallelogramma.html

Калькулятор периметра параллелограмма через диагонали

Параллелограмм — четырехугольник, стороны которого являются попарно параллельными отрезками. Параллелограмм представляет собой фигуру, частными случаями которой являются ромб, прямоугольник и квадрат — четырехугольники, знакомые нам с самого детства.

Геометрия параллелограмма

Четырехугольник считается параллелограммом, если соблюдается хотя бы одно из нижеперечисленных условий:

• противоположные стороны параллельны друг другу;
• противоположные стороны равны друг другу;
• пересекающиеся диагонали в точке пересечения делятся пополам.

Параллелограмм и его частные случаи — наиболее встречающаяся в реальной жизни фигура.

В трехмерном пространстве параллелограмм превращается в четырехугольную призму, форму которой имеет большинство рукотворных объектов: кирпичи, системные блоки компьютеров, стены, книги или коробки.

Параллелограмм также можно увидеть прямо на улице. Прямоугольные или косоугольные окна — это параллелограммы. Кроме того, прямо под ногами вы можете увидеть один из наиболее банальных воплощений ромба в реальности — тротуарную плитку. Столь широкое распространение данной фигуры в повседневной жизни делает вопрос определения площади и периметра параллелограмма актуальной задачей.

Периметр параллелограмма

Периметр представляет собой количественную оценку общей длины сторон любой фигуры. Параллелограмм имеет четыре стороны, которые попарно равны и параллельны друг другу. Исходя из этого, периметр геометрической фигуры выражается простой формулой:

P = 2 (a + b)

Путем подстановок мы можем найти стороны геометрической фигуры при помощи диагоналей и одной из ее высот. Наш онлайн-калькулятор позволяет определить периметр параллелограмма, зная три переменных: две диагонали и высоту четырехугольника.

Естественно, что вы можете воспользоваться и самой простой формулой для подсчета периметра, однако программный код калькулятора требует введения 3 переменных, поэтому для его корректной работы помимо длин сторон введите значение высоты, равное ha = b или hb = a.

К примеру, если a = 3, b = 4, то укажите, что hb = 3 или ha = 4. Такая подстановка превратит параллелограмм в квадрат, однако при известных сторонах периметр не зависит от величины углов геометрической фигуры, что позволит нам корректно рассчитать требуемый параметр.

Рассмотрим пару примеров.

Примеры из жизни

Пример №1

Давайте определим периметр четырехугольника, зная, что его диагонали равны 3 и 5 см, а высота фигуры составляет 2 см. Свойства четырехугольника подсказывают нам, что высота численно не может быть больше длин диагоналей, поэтому параметр h всегда меньше и d1, и d2. Введем эти данные в форму калькулятора и получим мгновенный ответ:

P = 11,45 см

Зная эти переменные, мы можем определить периметр любого параллелограмма.

Пример №2

Определить периметр абстрактного параллелограмма можно и по стандартной, самой простой формуле. Если стороны четырехугольника равны a = 3 и b = 4, то нам понадобится ввести эти данные в калькулятор, а также указать, что ha = 4. Мы получим ответ в виде:

P = 14,

что полностью соответствует расчетам по классической формуле P = 2 (a + b).

Заключение

Параллелограмм и его частные случаи занимают в деятельности человека важное место.

В реальной жизни вам понадобится определять периметры и площади прямоугольников, квадратов, ромбов или параллелограммов, которые являются гранями соответствующих призм или полноценными фигурами на плоскости.

Используйте наши калькуляторы для выполнения расчетов при решении повседневных, школьных или профессиональных задач.

Источник: https://BBF.ru/calculators/131/

Как найти периметр параллелограмма

В школьной программе, по геометрии, можно часто встретить задания, в которых необходимо найти периметр параллелограмма. Для его нахождения нужно использовать всего лишь одну простую формулу.

1

Что такое параллелограмм?

• Параллелограмм – в переводе с греческого означает параллельный.
• По своей структуре параллелограмм – это четырехугольник, стороны которого параллельны друг другу. Две его боковые стороны ложатся наискось. Каждая из сторон равна друг другу, т. е, равны противоположные углы. Но каждая из прилегающих сторон может отличаться размером.
• В основном четырехугольник обозначается большими заглавными буквами ABCD.
• Еще одной особенностью параллелограмма, является тот факт, что он может являться квадратом, прямоугольником или ромбом.
• Чтобы вычислить является ли четырехугольник параллелограммом, необходимо использовать правила нахождения параллелограмма. Одним из таких  правил является тот факт, когда его диагонали пересекаются и точкой пересечения делятся пополам.
• Считается, что общая сумма углов, которые лежат параллельно, должна равняться 180 °С, т.е. A + B + C + D = 180 °С. Чтобы вычислить, нужно использовать правило параллельных прямых.

2

Что такое площадь параллелограмма?

• Площадью параллелограмма называется геометрическая фигура, у которой есть основание, высота, а также боковые стороны равны между собой.
• Для того, чтобы приступить к вычислению площади параллелограмма необходимо знать его высоту, а также измерить боковые стороны.
• Существуют специальные теоремы и доказательства, при помощи которых легко вычислить площадь параллелограмма.

3

Как найти периметр параллелограмма?

• Чтобы найти общую численную характеристику параллелограмма необходимо использовать формулу. Такая формула может изменяться, зависимости от заданных значений.
• Чтобы найти периметр необходимо воспользоваться основной формулой: P = 2 * (a + b), где а – верхняя сторона, b – боковая сторона.
• Например, одна из боковых сторон параллелограмма  – а равна 4 см, а сторона b, которая перпендикулярно ей  – 6 см. Вычисли периметр, используя формулу: a = 6 см, b  = 4 см. P = 2 * (6+4) = 10 * 2 = 20 см.
• Значит, периметр данного параллелограмма будет равен 20 см.
• Значение периметра может измеряться при помощи единицы измерения длины.
• Периметр параллелограмма всегда равен удвоенной сумме двух его сторон.

Кроме периметра, также при помощи формул можно найти любое значение данной геометрической фигуры: высоту, площадь, площадь по вписанной окружности и другие необходимые параметры.

Источник: https://sovetclub.ru/kak-najti-perimetr-parallelogramma