Подборка по базе: 3 курс_Тесты по теме АБСЦЕССЫ БО.odt, Шкаленкова К.В. курсовая.docx, Зилинский, курсовая работа.docx, Тема 4.1 (ОМ — 5 курс, рус).docx, Менеджмент в туризме тесты 4 курс.docx, 1 Курс.docx, Планы семинарских ГР право часть 2. Для 3 курса.
doc, История Болезни Урология 4 курс.docx, Занятие №12 Эклампсия Пр. 2 курс.docx, легкая атлетика 2 курс.doc.
- МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
- КОЛЕБАНИЯ И ВОЛНЫ
- Краткий курс лекций.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА»А.А.
Олешкевич
| Кафедраинформационных технологий,математики и физики. |
Москва 2014
УДК 531.13(07)ФГБОУ ВПО МГАВМ и Б Олешкевич А. А. Колебания и волны..
Утверждены методической комиссией ветеринарно-биологического факультета в качестве краткого курса лекций по физике для самостоятельного изучения темы и выполнения контрольных работ студентами всех факультетов очного, заочного и очно-заочного (вечернего) отделений МГАВМ и Б. Протокол № 6 от 19 марта 2014 года.
Москва — 2014Издательство «Капитал-принт», 2014.Изд. лиц. ЛР№02159
Подписано в печать 1 апреля 2014 года
Бумага «Айсберг». Формат А5. Гарнитура «Таймс»
Печать ризографическая. Усл.п.л. 1,6. Тираж 500 экземпляров.
ВВЕДЕНИЕ
Колебания и волны являются неотъемлемой частью жизни людей и большинства животных. Именно волны находятся в основе сердечных процессов, благодаря которым человек существует. Кровь циркулирует по телу, подгоняемая сокращениями сердца. А мышечные сокращение – это колебательные движения.
Когда одна область начинает колебаться между разными состояниями, она неизбежно затрагивает соседнюю область – возникает движение. Биение сердца происходит благодаря низковольтному разряду электрического тока, который постоянно проходит через клети.
Еще одним ярким примером волн в организме является перистальтическая волна, которая подхватывает пищу во время глотания и направляет через пищевод в желудок. Эта же самая волна мышечных сокращений двигает пищу из желудка дальше в тонкий кишечник, где питательные вещества всасываются.Работа мозга также не обходится без участия волн.
Но это не волновые сокращения мышц, а крошечные, длящиеся всего долю секунды электрохимические реакции – импульсация нейронов. Любые звуки являются акустическими волнами. Нам доступна лишь малая часть всех акустических волн – большая часть не воспринимается нашим ухом.Также волны могут нести в себе информационную составляющую.
Микроволновое излучение уже поведало много интересного о происхождении и составе Вселенной, а также позволило человечеству греть еду в «микроволновке», говорить по сотовому телефону, выходить с ноутбуков в Интернет, устанавливать беспроводные соединения с помощью Bluetooth, дало возможность GPS-навигации и осуществление связи Земли со спутниками в целом.
Помимо полезных и необходимых для нормальной жизнедеятельности волн встречаются волны губительные. Взрывная волна сильно влияет на деятельность мозга даже при отсутствии видимых внешних повреждений. Цунами уносят сотни тысяч жизней и смывают прибрежные районы, оставляя за собой полную разруху.
Исходя из всего перечисленного выше, можно сделать вывод, что знание закономерностей, природы, свойств колебаний и волн дает возможность улучшать качества жизни, выходить на новые технологические уровни, своевременно заботиться о здоровье человека и животных, предотвращать или предсказывать природные катаклизмы. На что и нацелено данное методическое пособие.
Раздел 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательным движением (колебаниями) называют всякий процесс, который обладает свойством повторяемости во времени. Периодическим называется движение, при котором физические величины, характеризующие колебательную систему, через равные промежутки времени принимают одни и те же значения.
При колебательном движение тело (материальная точка) перемещается вблизи устойчивого положения равновесия, отклоняясь то в одну, то в другую сторону. При этом через любую точку траектории, за исключением крайних, тело проходит как в прямом, так и в обратном направлении.
Следовательно, отличительным признаком колебательного движения является его возвратность. Например, механическим колебательным движением является: движение тела, подвешенного на нити (маятник), колебания тела, подвешенного на пружине (пружинный маятник), колебания струн, вибрации фундаментов зданий.
Таким образом, отличительными признаками колебательного движения являются: 1) повторяемость движения; 2) возвратность движения (движение как в прямом, так и в обратном направлении).
Для существования механических колебаний необходимо:
Наиболее важными величинами, характеризующими механические колебания, являются:
- число колебаний за некоторый промежуток времени t. Обозначается буквой N;
- координата материальной точки или ее смещение (отклонение) — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени. Обозначается буквой x, измеряется в метрах (м);
- амплитуда — максимальное смещение тела или системы тел из положения равновесия. Обозначается буквой A или xmax, измеряется в метрах (м);
- период — время совершения одного полного колебания. Обозначается буквой T, измеряется в секундах (с);
- частота — число полных колебаний в единицу времени. Обозначается буквой ν, измеряется в герцах (Гц);
- циклическая частота, число полных колебаний системы в течение 2π секунд. Обозначается буквой ω, измеряется в радиан в секунду (рад/с);
- фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Обозначается буквой φ, измеряется в радианах (рад);
- начальная фаза — аргумент периодической функции, определяющий значение физической величины в начальный момент времени (t = 0). Обозначается буквой φ0, измеряется в радианах (рад).
Эти величины связаны между собой следующими соотношениями:
![]()
![]()
Тема 1. Гармонические колебания.
Гармонические колебания — это колебания, при которых координата (смещение) тела изменяется со временем по закону косинуса или синуса и описывается формулами:
![]()
Зависимость координаты от времени x(t) называется кинематическим законом гармонического колебания (законом движения). Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).
Пусть тело совершает колебания по гармонические закону (φ0 = 0). На рисунке 1 представлен график зависимости координаты x от времени t.
Выясним, как изменяется проекция скорости колеблющейся точки со временем. Для этого найдем производную по времени от закона движения:![]()
где ![]() — амплитуда проекции скорости на ось x. Эта формула показывает, что при гармонических колебаниях проекция скорости тела на ось x изменяется тоже по гармоническому закону с той же частотой, с другой амплитудой и опережает по фазе смешение на π/2 (рис. 2).
— амплитуда проекции скорости на ось x. Эта формула показывает, что при гармонических колебаниях проекция скорости тела на ось x изменяется тоже по гармоническому закону с той же частотой, с другой амплитудой и опережает по фазе смешение на π/2 (рис. 2).
Для выяснения зависимости ускорения ax(t) найдем производную по времени от проекции скорости:
![]()
![]() (1)
(1)
где ![]() — амплитуда проекции ускорения на ось x.
— амплитуда проекции ускорения на ось x.
При гармонических колебаниях проекция ускорения опережает смещение по фазе на π (рис.3).
Аналогично можно построить графики зависимостей x(t), υx(t) и ax(t), если (φ0 = 0).
- Учитывая, что из уравнения (1) для ускорения можно записать
т.е. при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, ускорение направлено в сторону, противоположную смещению.
Данное соотношение можно переписать в виде
Последнее равенство называют уравнением гармонических колебаний.
Физическую систему, в которой могут существовать гармонические колебания, называют гармоническим осциллятором, а уравнение гармонических колебаний — уравнением гармонического осциллятора.
Тема 2. Затухающие колебания
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются.
Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией.
Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.
График затухающих колебаний (меняется по экспоненте):
Тема 3. Вынужденные колебания. Резонанс
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
- Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
- Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:
Резонанс — (фр. resonance, от лат.
resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.График зависимости вынужденных колебаний от частоты.
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника.
Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках). Резонансные явления могут вызвать необратимые разрушения в различных механических системах.
Резонансный контур лежит в основе принципа действия мобильного телефона, ноутбука с адаптером беспроводной сети, автомобильного радиоприемника или даже такого устройства, как радионяня.
Тема 4. Сложные колебания
Всякое сложное колебание состоит из ряда простых синусоидальных колебаний — основного и высших гармоник. Форма сложного колебания может быть самой различной, в зависимости от того, сколько гармоник входит в его состав, какие у них частоты, амплитуды и начальные фазы. Примером сложных колебаний служит электрокардиограмма и электроэнцефалограмма.
Электрокардиограмма в 12 стандартных отведениях у мужчины 26 лет, без патологии.
Раздел 2. УПРУГИЕ ВОЛНЫ.
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.
Механизм возникновения волн. На рисунке показано движение частиц при распространении в среде поперечной волны. Номерами 1, 2 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии 1/4 T, т.е. расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами.
В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигнет крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2.
По прошествии еще четверти периода частица 1 будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица 2 достигнет крайнего верхнего положения, а частица 3 начнет смещаться вверх из положения равновесия.
В момент времени, равный T, частица 1 закончит полный цикл колебания, и будет находиться в таком же состоянии движения, как и в начальный момент времени. Волна к моменту времени T достигнет частицы 5.
На рисунке показаны колебания частиц, положения, равновесия которых лежат на оси x. В действительности колеблются не только частицы, расположенные вдоль оси x, а совокупность частиц в некотором объёме.
Распространяясь от источника колебаний, волновой процесс охватывает всё новые и новые части пространства.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом).
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом.
Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы.
Соответственно волна в этих случаях называется плоской или сферической.
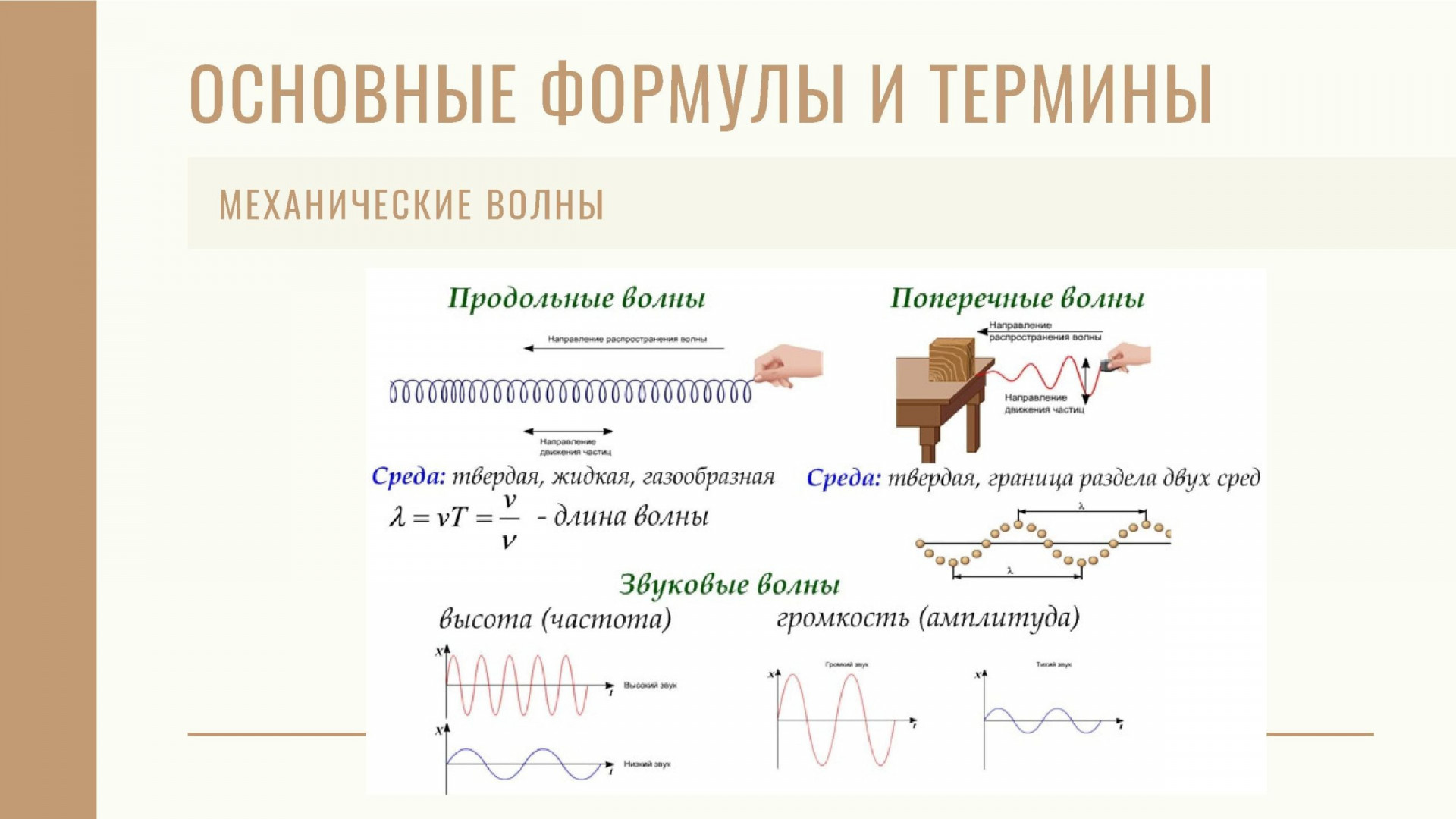
Расстояние λ, на которое распространяется волна за время, равное периоду колебания частиц среды, называется длиной волны. Очевидно, что: λ=vT ,
где v— скорость волны, T— период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющихся с разностью фаз, равной 2π. Заменив T через 1/ν, где v — частота колебаний, получим связь между длиной волны, частотой колебаний и скоростью распространения волны: λν=v.
Продольная волна – это волна, в которой частицы среды колеблются вдоль направления распространения волны. Поперечная— это волна, в которой частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.
Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна).
Отраженная от него волна наложится на падающую волну.
Источник: https://topuch.ru/kolebaniya-i-volni-kratkij-kurs-lekcij/index.html
Механические колебания и волны

Лекция № 2
Механические колебания и волны. Акустика.

План лекции:
- Колебания и их виды. Уравнение колебаний.
- Периодические механические процессы в организме.
- Механические волны. Уравнение волны.
- Звук. Субъективные и объективные характеристики звука.
- Физические основы звуковых методов исследования в клинике.

Колебательным движением называется такое, при котором значения физических величин, характеризующих это движение, повторяются во времени.

Виды колебаний:
- Если величины, характеризующие колебания, повторяются через равные промежутки времени, то колебание называется периодическим .
- Гармонические колебания – это движение, в котором ускорение направленно к положению равновесия и пропорционально отклонению тела от этого положения.

Гармонические колебания
- свободные (затухающие и незатухающие)
- вынужденные
- автоколебания

Свободными колебаниями называют такие колебания, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии.

Свободные колебания

Движение маятника при небольших амплитудах колебания является гармоническим при следующих условиях:
- Наличие положения равновесия
- Наличие силы, направленной к положению равновесия и пропорциональной отклонению тела от этого положения
- Наличие инерции колеблющегося тела

Основной величиной, характеризующей колебание, является смещение, т.е. расстояние колеблющегося тела от положения равновесия в любой заданный момент времени. Важнейшим признаком простого колебания является изменение смещения во времени по закону синуса или косинуса.

Уравнение незатухающих колебаний
- А – амплитуда
- ω – круговая частота колебаний
- φ – начальная фаза
- ω t + φ – фаза колебаний
Затухающие колебания
- В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется, и колебание становится затухающим.
Уравнение затухающих колебаний
- А – амплитуда
- ω – круговая частота собственных колебаний
- φ – начальная фаза
- ω t + φ – фаза колебаний
- β – коэффициент затухания
Сложение гармонических колебаний
- Материальная точка может одновременно участвовать в нескольких колебаниях. Чтобы найти траекторию результирующего движения, следует сложить смещения всех колебаний. При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу.
Вид фигуры Лиссажу зависит как от соотношения амплитуды А 1 и А 2 , так и от отношения частот ω 1 / ω 2 и разности начальных фаз φ 1 — φ 2 слагаемых колебаний.
Совокупность гармонических колебаний, на которые разложено сложное колебание, называется гармоническим спектром сложного колебания.
Сложное колебание и его гармонический спектр
- Ж. Фурье показал, что периодическая функция любой сложности может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции.
Такое разложение периодической функции на гармонические составляющие и следовательно, разложение различных периодических процессов на гармонические колебания называется гармоническим анализом.
Вынужденными колебаниями называются колебания тела, вызванные и поддерживаемые внешней силой (вынуждающей), периодически изменяющейся по величине и направлению.
- Амплитуда вынужденного колебания прямо пропорциональна амплитуде вынуждающей силы и имеет сложную зависимость от коэффициента затухания среды и круговых частот собственного и вынужденного колебаний.
Увеличение амплитуды колебаний тела при совпадении его собственной частоты с частотой внешней периодической силы называется резонансом .
Резонанс – достижение максимальной амплитуды вынужденных колебаний для заданных ω и β
- Если ω и β системы заданы, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называется резонансной.
Незатухающие колебания, существующие в какой-либо системе с затуханием при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы – автоколебательными.
Периодические механические процессы в организме (автоколебания)
- Дыхательные движения грудной клетки
- Сокращение и расслабление мышцы сердца
- Пульсовое колебание стенок артерий
Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.
Механические волны делятся на 2 вида:
- Упругие волны, возникающие благодаря связям, существующим между частицами среды
- Волны на поверхности жидкости
Уравнение механической волны
Где:
- φ = ω ( t-x/v ) – фаза волны
Звук.
- Колебания частиц в упругих средах, распространяющиеся в форме продольных волн, частота которых лежит в пределах, воспринимаемых человеческим ухом, в среднем от 16 до 20000 Гц, называются звуковыми колебаниями или просто звуком .
Виды звука:
- Тон – звук, являющийся периодическим процессом.
- Шум – звук, отличающийся сложной неповторяющейся временной зависимостью.
- Звуковой удар – это кратковременное звуковое воздействие: хлопок, взрыв.
Объективные характеристики звука
- Частота
- Амплитуда колебаний
- Форма колебаний
- Гармонический спектр
- Интенсивность звука
- Звуковое давление
Субъективные характеристики звука
- Высота – определяется высотой основного тона
- Тембр – определяется спектральным составом
- Громкость – характеризует уровень слухового ощущения
Звуковые методы исследования в клинике
- Аудиометрия
- Фонокардиография
Физические основы звуковых методов исследования в клинике
- Аудиометрия – метод измерения остроты слуха (абсолютных порогов слухового ощущения) на разных частотах при помощи аудиометра.
Абсолютный порог слухового ощущения – минимальная интенсивность звука, вызывающая слуховые ощущения.
I =10 -12 Вт/м 2
Физические основы звуковых методов исследования в клинике
- Фонокардиография – графический метод регистрации тонов и шумов сердца с их последующей диагностической интерпретацией.
- Запись фонокардиограммы производится при помощи фонокардиографа.
Физические основы звуковых методов исследования в клинике
- Аускультация – звуковой метод диагностики, основанный на выслушивании различных звуков при помощи фонедоскопа.
- Фонедоскоп состоит из полой капсулы, с передающей звук мембраной, прикладываемой к телу пациента, от нее идут резиновые трубки к уху врача.
Физические основы звуковых методов исследования в клинике
- Перкуссия – метод исследования внутренних органов посредством постукивания по поверхности тела и анализа возникающих при этом звуков. Простукивание производится с помощью специального молоточка с резиновой головкой и пластинки из упругого материала, называемой плессиметром, которую при ударе накладывают на поверхность тела. Пользуются просто простукиванием кончиком согнутого среднего пальца право руки по 2 фаланге среднего пальца левой руки, наложенного на тело больного.
Источник: https://videouroki.net/razrabotki/miekhanichieskiie-koliebaniia-i-volny.html
Механические колебания и волны – FIZI4KA
ЕГЭ 2018 по физике ›

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин. Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения. Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно! Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
![]()
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний Скорость гармонических колебаний есть первая производная координаты по времени:
![]()
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний Ускорение гармонических колебаний есть первая производная скорости по времени:

где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
- Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
- Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
- Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
- При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно. В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно! Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия. Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени. Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний. Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно! Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания. Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени. Обозначение – (
u ), единицы времени – с-1 или Гц (Герц).
- 1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
- Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд. Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими. Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
- Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
- Период колебаний математического маятника:
- Частота колебаний математического маятника:
- Циклическая частота колебаний математического маятника:
- Максимальное значение скорости колебаний математического маятника:
- Максимальное значение ускорения колебаний математического маятника:
- Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
- Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
- Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
- Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
- где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
- Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
- Период колебаний пружинного маятника:
- Частота колебаний пружинного маятника:
- Циклическая частота колебаний пружинного маятника:
- Максимальное значение скорости колебаний пружинного маятника:
- Максимальное значение ускорения колебаний пружинного маятника:
- Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
- Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно! Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
- Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
- Условие резонанса:
- ( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением.
Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях. Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах. Обозначение – ( lambda ), единицы измерения – м.
- Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
- Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук ((
u ) < 16 Гц); - звуковой диапазон (16 Гц < ( u ) < 20 000 Гц);
- ультразвук ((
u ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
- в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.
- Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны. Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Источник: https://fizi4ka.ru/egje-2018-po-fizike/mehanicheskie-kolebanija-i-volny-2.html
Механические колебания и волны — Механика — Теоретический материал для подготовки к ЕГЭ
Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина х изменяется по закону синуса или косинуса, т.е.:
![]()
Величина А, равная наибольшему абсолютному значению колеблющейся физической величины х, называется амплитудой колебаний. Выражение ![]() определяет значение х в данный момент времени и называется фазой колебаний. Периодом Т называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебанийназывают число полных колебаний, совершенных за единицу времени:
определяет значение х в данный момент времени и называется фазой колебаний. Периодом Т называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебанийназывают число полных колебаний, совершенных за единицу времени:
Частота измеряется в с-1. Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому ее концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле:

где l — длина маятника.
Период колебаний груза на пружине определяется по формуле:

где k — жесткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между ее частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
- Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
- где v — скорость распространения волны.
- Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/с.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
Источник: https://compendium.su/physics/ege/7.html
Конспект урока "Механические колебания и волны"
- Механические колебания и волны
- Урок обобщения в 9 классе
- Цели урока:
- обобщить, закрепить знания учащихся по данной теме, совершенствовать навыки решения качественных и расчетных задач;
- научить видеть проявления изученных закономерностей в окружающем мире, способствовать расширению кругозора учащихся;
- формировать навыки коллективной работы в сочетании с самостоятельностью учащихся.
- Эпиграф: «Рожденный пустыней,
- Колеблется звук,
- Колеблется синий
- На нитке паук.
- Колеблется воздух,
- Прозрачен и чист,
- В сияющих звездах
- Колеблется лист».
- Н. Заболоцкий
- Ход урока:
-
Мотивация познавательной деятельности.
- Академик Папалекси сказал: «Не будет преувеличением сказать, что среди процессов, как в свободно протекающих в природе, так и используемых в технике, колебания, понимаемые в широком смысле этого слова, занимают во многих отношениях выдающееся и часто первенствующее место».
- И наш урок сегодня посвящен повторению темы «Колебания и волны».
- Для повторения основных понятий разгадаем кроссворд «Поднимись по ступенькам»
-
Метод определения расстояния до различных предметов и обнаружение их месторасположения с помощью звуковых волн.
-
Колебания с частотой более 20000Герц.
-
Колебания, частота которых меньше 16 Герц.
-
Модуль наибольшего смещения тела от положения равновесия.
-
Явление резкого возрастания амплитуды колебаний.
-
Число колебаний за 1с.
-
Время, за которое совершается одно полное колебание.
-
Процесс распространения колебаний в среде с течением времени.
-
Прибор для измерения времени.
-
Естественный приемник звука.
А) Решение качественных задач
Зачитываю правильные и неправильные утверждения, а учащиеся либо подтверждают их, либо опровергают.
-
Верите ли вы, что самолет может развалиться в воздухе? (Да)
-
На Луне произошел сильный взрыв. Будет ли он слышен на Земле? (Нет)
-
Верите ли вы, что комар машет крыльями быстрее, чем шмель? (Да)
-
Из арабской сказки «Рассказ о Хасибе и царице змей» : Хасиб Карим – Аддин ушел от них и сел один в той пещере. И стал он ударять по земле топором. И услышал он из – под топора, по звуку, что земля пустая, и поняв, что под землей пусто, принялся копать и через некоторое время увидел круглую плиту, в которой было кольцо…»
Какие еще примеры метода выстукивания вы знаете? (контроль вагонных колес, стеклянной и фарфоровой посуды в магазине, при осмотре пациентов в поликлинике).
-
Из американской сказки «Гора – будильник»: однажды я жил у реки, а напротив была гора. Она была так далеко, что если крикнуть, то эхо возвращается лишь через 16 часов. Я живо смекнул, что к чему. Бывало, когда ложусь спать, кричу погромче «Пора вставать!» А через 6 часов под утро, эхо как крикнет над ухом «Пора вставать!» Ну я и вставал. Можно ли верить рассказчику? (Нет).
Б) Решение рассчетных задач.
Для решения рассчетных задач необходимо знать формулы. Следующее задание «Допиши формулу». (Раздаю учащимся карточки с формулами, в которых недостает обозначения какой – либо величины, задача учащихся правильно вставить недостающую букву. Например Т=1/*; λ=*/ν; ν=*/Т).
Применение знаний в конкретных ситуациях. Индивидуальная работа. Раздаю карточки с дифференцированными заданиями. Учащиеся самостоятельно выбирают уровень сложности и выполняют задания. (Один из вариантов).
Уровень «3»
-
Пружинный маятник совершил 16 колебаний за 4с. Определите период и частоту колебаний.
-
Определите длину звуковой волны при частоте 200Гц, если скорость распространения волны 340м/с.
Уровень «4»
-
Пружинный маятник совершает колебания за 2с. Масса груза 200г. Определите жесткость пружины.
-
В каких упругих средах могут возникать поперечные волны?
Уровень «5»
-
Длина волны в воздухе 17см при скорости 340м/с. Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02м.
-
Математический маятник длиной 1м совершает колебания с частотой 0,5Гц. Чему равно ускорение свободного падения в месте наблюдения?
В) Работа в группах. Экспериментальное задание.
1 группа. Определить экспериментальным путем зависит ли период нитяного маятника от его длины?
(Указание: измерить время 30 колебаний маятника длиной 1м и вычислить период. Уменьшить длину маятника в 4 раза и вновь определить период. Сделать вывод).
2 группа. Определить экспериментальным путем зависит ли период нитяного маятника от его массы?
(Указание: не меняя длину маятника, определить периоды колебаний маятника, для случаев, когда его масса 100г, 200г, 300г).
- Составление кластера по теме «Колебания и волны»;
- Выставление отметок (отметки выставляются суммарно за несколько видов работ учащегося, отмечаются наиболее активные).
Повторить основные понятия и формулы темы §17-27, подготовиться к контрольной работе.
Источник: https://multiurok.ru/files/konspiekt-uroka-miekhanichieskiie-koliebaniia-i-vo.html
План-конспект урока по физике по теме: Механические колебания | Социальная сеть работников образования
Тема: «Механические колебания»
Цель урока:
- Познакомиться с новым видом движения.
- Ввести характеристики колебательного движения.
- Задачи:
- Обучающая – сформировать у учащихся представления о колебательном движении; изучить свойства и основные характеристики периодических (колебательных) движений.
- Развивающая – развивать умения и навыки анализировать знания и делать выводы; развитие речи учащихся через организацию диалогического общения на уроке; развитие и поддержка внимания учащихся через смену учебной деятельности.
- Воспитательная – формировать познавательный интерес; воспитывать дисциплинированность, трудолюбие, внимательность.
- Тип урока: комбинированный.
- Ход урока.
- Организационный момент. Объявление темы урока.
- Анализ контрольной работы.
- Изучение нового материала.
Переходя к изложению нового материала, можно сразу показать два типа периодических движений. Это – движение груза, закрепленного на нити, и груза на пружине.
- Математический маятник – тело, подвешенное на нити, размеры которого много меньше длины нити.
- Пружинный маятник – груз, прикрепленный к пружине.
- Эти два вида движения отличаются от поступательного движения тем, что эти движения являются периодическими.
- Такой тип механического движения, когда тело за определенные промежутки времени старается повторить свое движение, проходя при этом положение равновесия, называется механическими колебаниями.
- Каждое движение характеризуется своими величинами.
— Какими величинами характеризуется равномерное прямолинейное движение? (Постоянной скоростью, координатой. Существует уравнение зависимости координаты от времени х = х0 + υхt.)
- — Какими величинами характеризуется равноускоренное прямолинейное движение?
- (Постоянным ускорением, координатой.)
- — Какими же величинами характеризуется колебательное движение?
- 1) Скоростью и ускорением.
При колебательном движении обе эти величины изменяются от точки к точке, от одного момента времени к другому. В точках максимального отклонения от положения равновесия скорость равна нулю. В точке равновесия скорость максимальна. Ускорение – наоборот.
- Период колебаний – время, за которое маятник совершает одно полное колебание.
[Т] = с Т =
- Частота колебаний – число полных колебаний в единицу времени.
[] = Гц =
- Амплитуда колебаний – наибольшее (по модулю) отклонение тела от положения равновесия. [А] = м.
- Связь периода колебаний с частотой: = или Т =
- Период математического маятника: Т = 2
- Период пружинного маятника: Т = 2
- Проверка понимания учащимися нового материала.
- Приведите примеры колебательных движений.
- Как вы понимаете утверждение о том, что колебательное движение периодично?
- Какие тела входят в колебательную систему, называемую пружинным маятником? Математическим маятником?
- Перечислите характеристики колебательного движения и дайте объяснение.
- Закрепление нового материала.
- Маятник совершил 20 колебаний за 1 мин 20 с. Найти период и частоту колебаний.
(Ответ: 4 с; 0,25 Гц.)
- Математический маятник длиной2,45 м совершил 100 колебаний за 314 с. Определить ускорение свободного падения для данной местности.
(Ответ: 9,8 м/с2)
- Информация о домашнем задании.
Источник: https://nsportal.ru/shkola/fizika/library/2014/03/06/mekhanicheskie-kolebaniya
Конспект урока "Механические колебания"
- МАОУ Дубровинская средняя общеобразовательная школа
- Урок в 11 классе по теме:
- Механические колебания, их характеристики.
- Математический маятник.
Разработан Евлановой С. Г.
- учителем физики,
- информатики
- 1 квалификационной
- категории
- Тема: Механические колебания, их характеристики.
- Математический маятник.
- Тип урока: урок первичного предъявления новых знаний.
- Цели урока:
- Личностные: занимать активную позицию на уроке, уметь слушать, принимать другую точку зрения, вести корректную дискуссию, уметь договариваться, работать в группе.
- Метапредметные: формировать у учащихся умения наблюдать и анализировать явления; способствовать развитию умений вести диалог, развивать логическое мышление.
- Предметные: познакомить учащихся с одним из наиболее распространённых движений в природе и технике – колебательным движением на примере математического маятника; ввести понятия характеристик колебательного движения; выяснить условия существования свободных колебаний;
- Оборудование: метроном, штативы, грузы, нить, мячик, проектор, компьютер, картинки.
- Структура урока и используемые технологии
| Этапы урока | Время | Используемые технологии | Приёмы и методы |
| I. Вступительно-мотивационный | 3 минуты | Создание ситуации успеха на уроке | Осмысление эпиграфа к уроку; упражнение «Те, кто…» |
| II. Постановка учебной проблемы | 3 минут | Технология развивающего обучения | Беседа; демонстрация опытов; постановка целей и задач урока |
| III. Изучение нового материала | 20 минут | Технология развития критического мышления | Работа в группах; демонстрация опытов; записи на доске и в тетрадях |
| IV. Закрепление нового материала | 15 минут | Технология интерактивного обучения | Эксперимент, работа в малых группах; работа с рисунками |
| V. Рефлексия. Домашнее задание | 4 минуты | Создание ситуации успеха | «Ладонь знаний»; осмысление легенды; комментарий по домашнему заданию |
- Ход урока
- „Я всегда хочу учиться, но не всегда хочу, чтобы меня учили».
- У. Черчилль
-
Вступительно-мотивационный этап урока.
Приветствие учащихся и контроль отсутствующих на уроке. План урока.
Учитель. Сначала я хочу провести с вами такое упражнение. Попрошу вас правильно реагировать на вопрос-задание.
Поднимите правую руку те, кто увлечён вопросами загадок и тайн природы, историей. Поднимите левую руку те, кто увлекается музыкой и танцами. А теперь поднимите обе руки те, кто увлечён компьютером. Захлопайте в ладоши те, кто увлекается спортом.
Вот и хорошо! Сегодня я буду работать с интересными учениками, которые занимают активную жизненную позицию. Эпиграфом к уроку я взяла слова У. Черчилля: «Я всегда хочу учиться, но не всегда хочу, чтобы меня учили». Как вы понимаете смысл этих слов.
Эти слова должны стать в каком-то роде девизом вашей учебной деятельности. (Поверьте, самостоятельно находить ответ на вопрос, разрешать проблемную ситуацию, наблюдать и анализировать, проводить опыты – это очень результативно и увлекательно. В процессе работы на уроке вы в этом убедитесь. Не бойтесь ошибиться при ответе на вопросы, т.к. не ошибается только тот, кто не работает).
II. Постановка учебной проблемы.
Беседа.
Учитель. Посмотрим такиедемонстрации: катится по столу мяч и движется стрелка метронома. В чём различия этих движений?
Учащиеся. Движение стрелки метронома – движение повторяющееся периодически.
Учитель.
Источник: https://kopilkaurokov.ru/fizika/uroki/konspiekt-uroka-miekhanichieskiie-koliebaniia






