Уравнение прямой, формулы и примеры

Содержание

Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.
Пример 1.
Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).
Решение:
1 способ — составим уравнение прямой с угловым коэффициентом.
Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:

Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.

Таким образом, y= -2x+3 — искомое уравнение.
2 способ — составим общее уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:

Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.

Умножив первое уравнение системы на -1 и сложив почленно со вторым:

получим: 5a-10b=0. Отсюда a=2b.

Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:
2bx+by-3b=0. Осталось разделить обе части на b:
2x+y-3=0.
Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:
y= -2x+3.
3 способ — составим уравнение прямой, проходящей через 2 точки.
Уравнение прямой, проходящей через две точки, имеет вид:
Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)
(то есть x1= -3, y1=9, x2=2, y2= -1):
и упростим:
По основному свойству пропорции
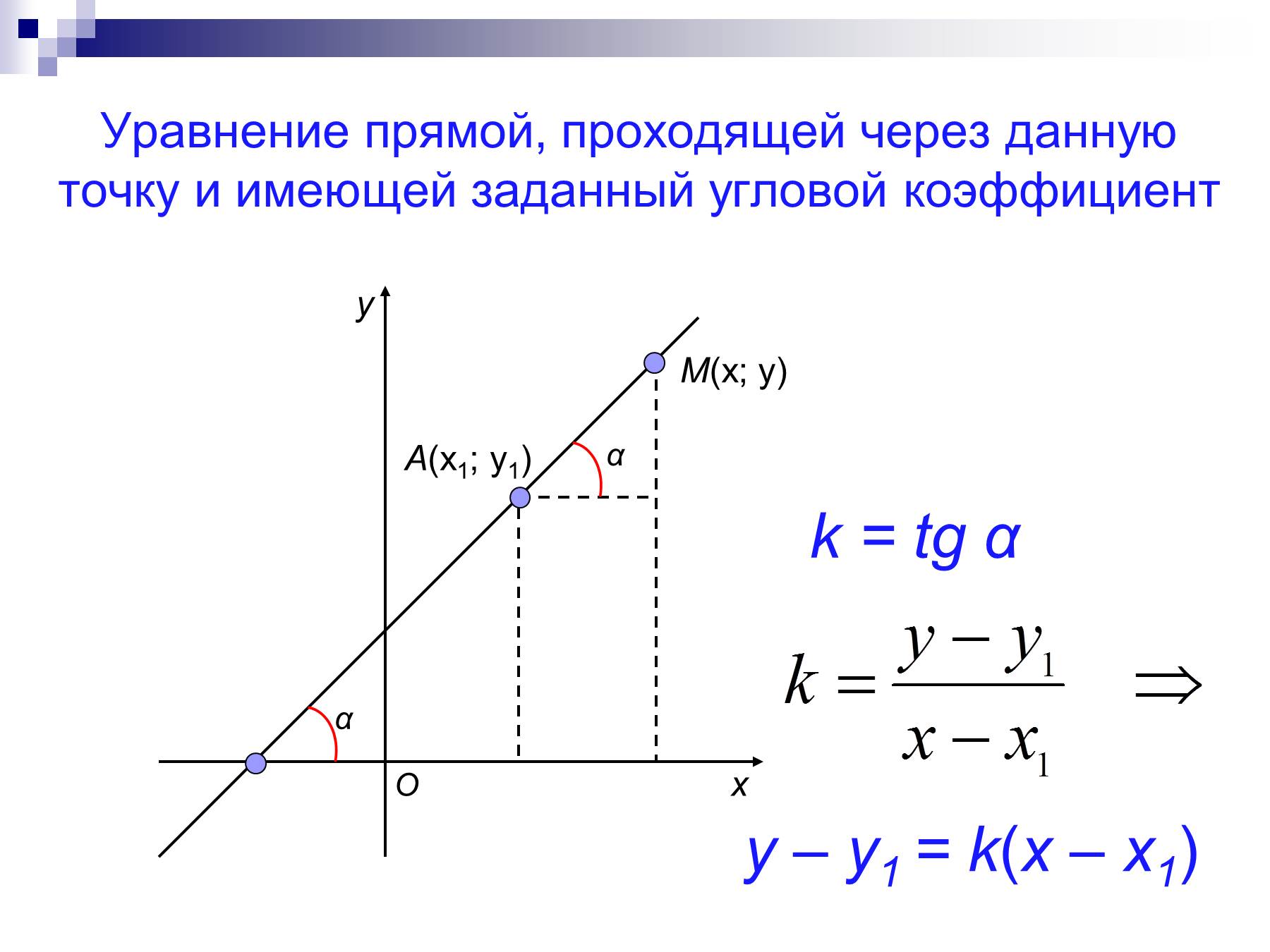
откуда 2x+y-3=0.

В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.

Замечание.
Если при подстановке координат заданных точек один из знаменателей уравнения
окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.
Пример 2.
Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).
Решение:
Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:
Пример 3.
Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).
Решение:

Источник: http://www.treugolniki.ru/sostavit-uravnenie-pryamoj/

Уравнение прямой

Уравнение прямой на плоскости

Уравнения прямой на плоскости в координатной форме

Любую прямую линию на плоскости можно задать общим уравнением прямой в декартовой системе координат:

то есть числа одновременно не равны нулю.

Прямая линия на плоскости может быть задана параметрическим уравнением прямой:

где числа не равны нулю одновременно. Числа являются компонентами направляющего вектора прямой — ненулевого вектора, лежащего на прямой.

Если то после исключения из уравнений прямой в параметрической форме параметра уравнение прямой приводятся к канонической форме:

Уравнение прямой, проходящей через две точки и :

При или это уравнение принимает соответственно вид или

Уравнения прямой на плоскости в векторной форме

Векторное уравнение прямой в параметрической форме:

$[ extbf{r} = extbf{r}_0 + extbf{a}t, qquad extbf{a} e extbf{0},]$

где — направляющий вектор прямой, — радиус-вектор некоторой точки прямой.

Нормальное векторное уравнение прямой:
$[left( extbf{r}- extbf{r}_0, extbf{n} ight) = 0, qquad extbf{n} e extbf{0},]$
где — вектор нормали к прямой.
Это уравнение также можно записать в форме

причём если вектор — единичный, то величина есть расстояние от точки до прямой. Вообще говоря, это уравнение имеет следующий смысл: проекция радиус-вектора любой точки прямой на нормаль к этой прямой постоянна.

Векторное уравнение прямой, проходящей через две различные точки:
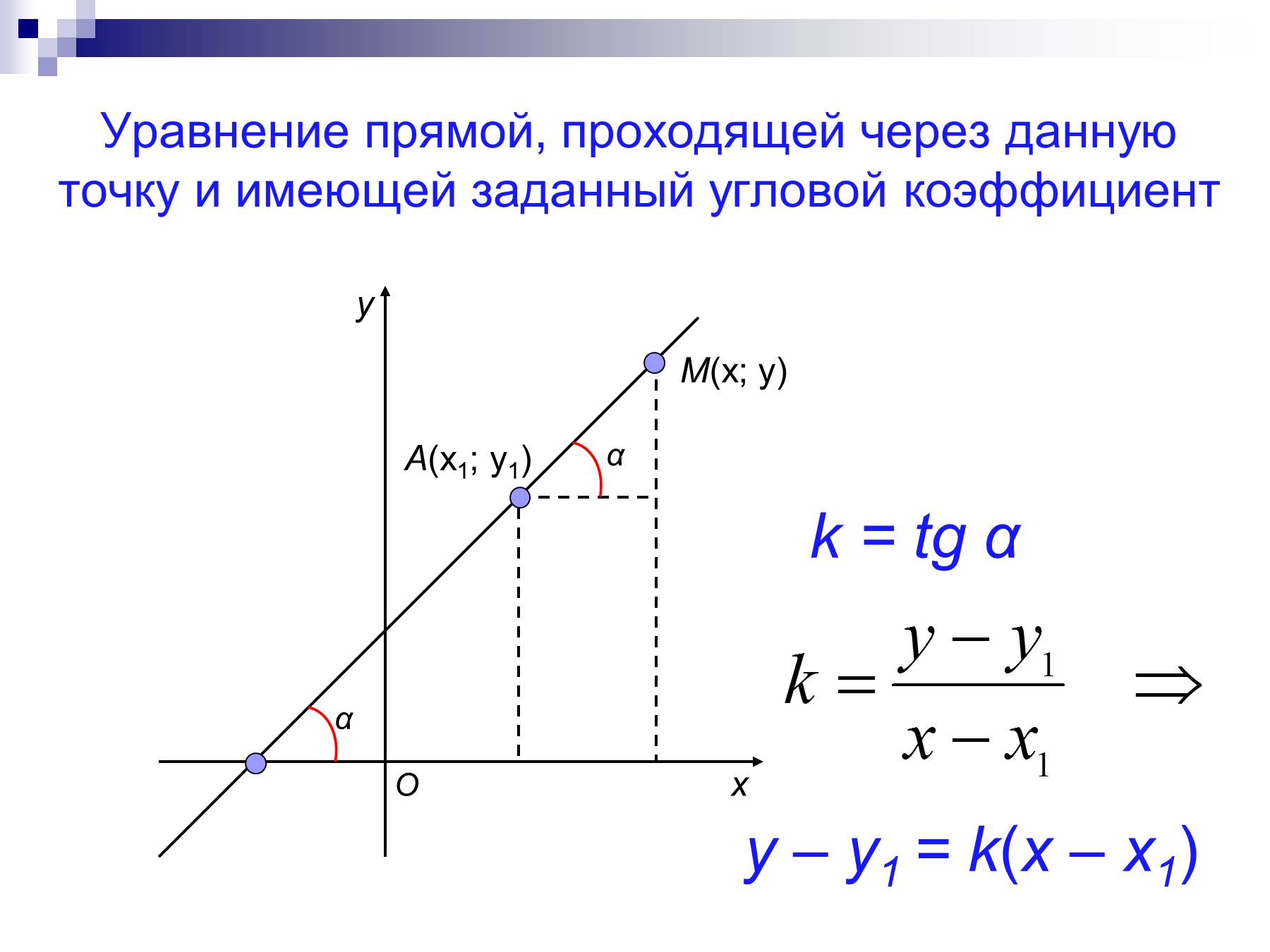
где и — радиус-векторы данных точек.

Это уравнение легко получается из векторного уравнения прямой в параметрической форме, если в качестве направляющего вектора прямой взять вектор

Уравнение прямой в пространстве

Уравнение прямой в пространстве в координатной форме

Прямая линия в пространстве может быть задана параметрическими уравнениями:

Числа являются компонентами направляющего вектора прямой.

Исключением параметра параметрические уравнения прямой приводятся к канонической форме:
Если, например, то канонические уравнения принимают вид
Аналогично для любой другой компоненты направляющего вектора.
Если два параметра равны нулю, например, то канонические уравнения имеют вид Аналогично для любых других пар компонент направляющего вектора.

Уравнение прямой в пространстве, проходящей через две точки и :
Если, например, то уравнения прямой принимают вид
Если к тому же то уравнения прямой записываются в виде Аналогично для любых двух пар совпадающих координат точек.

Прямая в пространстве может быть задана как пересечение двух непараллельных плоскостей:

Уравнение прямой в пространстве в векторной форме

Прямая линия в пространстве может быть задана уравнением в параметрической форме:

где — направляющий вектор прямой, — радиус-вектор некоторой точки прямой. Это уравнение совпадает с параметрическим векторным уравнением прямой на плоскости.

Прямую в пространстве можно задать векторными уравнениями:

или

Векторное уравнение прямой в пространстве, проходящей через две различные точки:

где и — радиус-векторы двух точек прямой.

Источник: https://umath.ru/theory/uravnenie-pryamoj/

4.1.8. Примеры решения задач по теме «Уравнение прямой на плоскости»

Задача 1.

Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у — 3 = 0. Найти координаты вершин этого параллелограмма.

Указание
Выясните, уравнения каких сторон даны в условии задачи: параллельных или
Смежных, и как расположена данная диагональ по отношению к данным сторонам.
Решение

Рис. 12
Выясним, уравнения каких сторон даны в условии задачи: параллельных или
Смежных.

Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.

Условие параллельности прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0: Уравнение прямой, формулы и примеры

Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:

Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:

Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.

Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:

Система уравнений для определения координат точки D составлена из уравнений прямых ADИ BD:

Остается найти координаты точки С. Составим уравнения прямых ВС и DC.

Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:

Тогда ВС можно задать уравнением

Аналогично АВ: У = -2Х – 3, KAB = -2 = KDC; DC: Y– 3 = -2(X– 3), 2X + Y – 9 = 0.

Найдем координаты точки С, решив систему из двух полученных уравнений:

Ответ: А(1; -2), В(0; -3), С(5; -1), D(3; 3).
Задача 2.
Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).
Указание
Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
1) провести прямую ВС;
2) провести через точку А прямую, перпендикулярную ВС;
3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Решение
Рис. 13
Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
4) провести прямую ВС;
5) провести через точку А прямую, перпендикулярную ВС;
6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Тогда точка А1 будет симметричной точке А относительно прямой ВС.
Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.
1) Найдем уравнение прямой ВС в виде:
2) Найдем угловой коэффициент прямой ВС:
Прямая АО Перпендикулярна прямой ВС, поэтому
Составим уравнение прямой АО:
3) Найдем координаты точки О как решение системы:
4) Точка О – середина отрезка АА1, поэтому
Ответ: (-4; 13).
Задача 3.
Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.
Указание
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2.
Решение
Рис. 14
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1
Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,
Ответ: 45о.

Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0
Справедлива формула:
.

Задача 4.
Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.
Указание
Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.
Решение
Рис. 15
Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:
Для ответа на вопрос задачи отметим, что:

1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);

2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).
Составим нормальные уравнения сторон треугольника АВС:
Вычислим соответствующие отклонения:
1) для точек М и А относительно прямой ВС:
2) для точек М и В относительно прямой АС:
3) для точек М и С относительно прямой АВ:

Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.

Ответ: Точка М расположена вне треугольника АВС.
Задача 5.
Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.
Указание
Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.
Решение
Рис. 16
1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:
Тогда уравнение медианы можно записать в виде:
2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:
Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.
Задача 6.
Определить, при каком значении А прямая
(А – 5)Х + (А2 – 1)У + 2А2 + 7А – 9 = 0

Параллельна оси ординат. Написать уравнение прямой.

Указание
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
В = 0, С ≠ 0.
Решение
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0

В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.

При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).
При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.
Ответ: 3Х + 7 = 0 при А = -1;
Задача 7.
Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.
Указание
Составьте уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».

Решение
Рис. 17
Составим уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:

Следовательно, условию задачи удовлетворяют три прямые:
Ответ:

Источник: http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-1-8-primery-resheniia-zadach-po-teme-uravnenie-priamoi-na-ploskosti

Общее уравнение прямой: описание, примеры, решение задач, общий вид уравнения прямой

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Общее уравнение прямой: основные сведения

Пусть на плоскости задана прямоугольная система координат Oxy.

Теорема 1

Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.

Доказательство

указанная теорема состоит из двух пунктов, докажем каждый из них.

Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.

Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.

Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0).

Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B).

Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.

Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.

Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.

Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Определение 1

Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy.

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.

Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Неполное уравнение общей прямой

Определение 2

Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.

Разберем все вариации неполного общего уравнения прямой.

Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Пример 1

Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:

A·27+C=0

Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0

Ответ: 7x-2=0

Пример 2

На чертеже изображена прямая, необходимо записать ее уравнение.

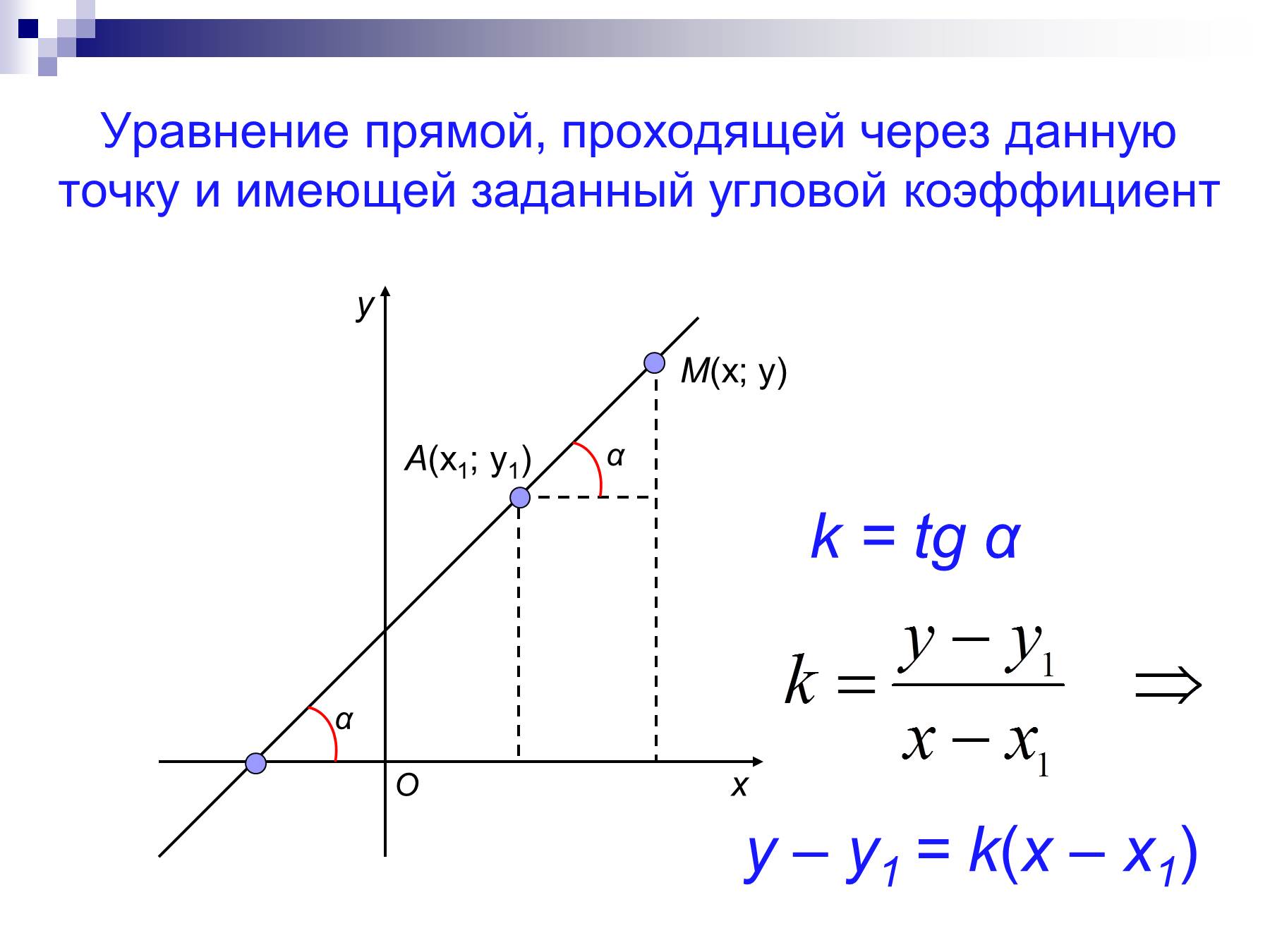
Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C.

Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля.

Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.

Ответ: y-3=0.

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0.

Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой.

Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Пример 3

Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.

Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор позволяет получить значения коэффициентов A и B, тогда:

Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0

Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 — 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x — 2·y + 11=0.

Ответ: x — 2·y + 11=0.

Пример 4

Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.

Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.

Это равенство возможно записать как пропорцию: x+CA-B=yA .

В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.

Перепишем равенство в виде пропорции: x-B=y+CBA .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Пример 5

Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.

Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.

Ответ: x-3=y-430.

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Пример 6

Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.

Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.

Пример 7

Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:

Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1

Пример 8

Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0

Пример 9

Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.

Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0

Пример 10

Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.

Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Пример 11

Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.

Пример 12

Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.

Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:

A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0

Ответ: 3x+5y=0.

Источник: https://Zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/

Матвокс ⋆ уравнение прямой (общее уравнение прямой) ⋆ энциклопедия математики

Любая прямая в декартовых координатах XOY имеет уравнение вида:

где a, b, c – некоторые числа, причем хотя бы одно из чисел a, b не равно нулю.

Данное уравнение называют общим уравнением прямой

Общее уравнение прямой

Рассмотрим произвольную прямую m на плоскости XOY.

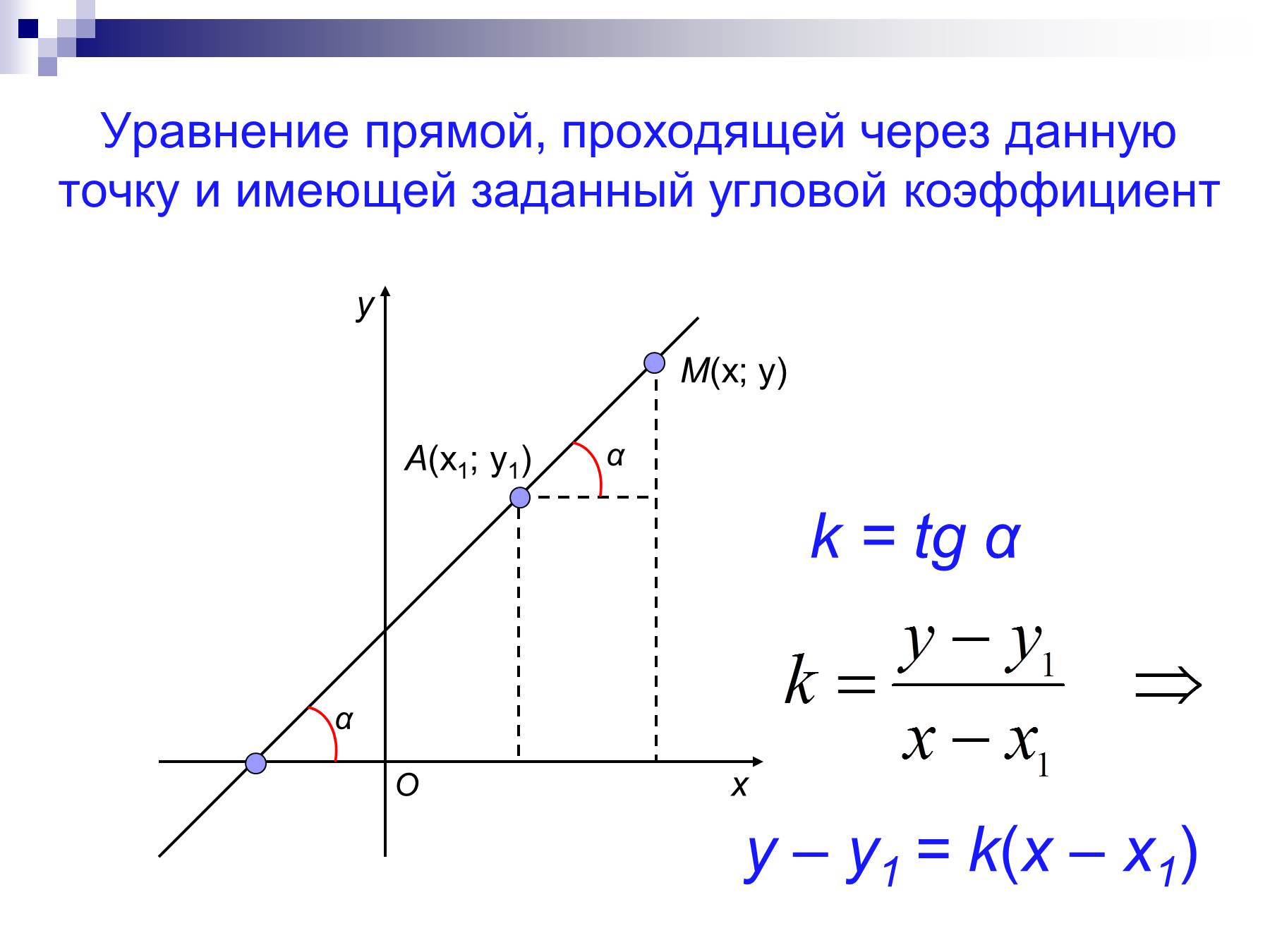
Вывод уравнения прямой. Шаг 1

Проведем какую-нибудь прямую n перпендикулярную прямой m.

Точку пересечения прямых обозначим буквой С.

Вывод уравнения прямой. Шаг 2

На прямой n отложим от точки С равные отрезки СА1 и СА2.

Пусть точки А1 и А2 имеют координаты:

Вывод уравнения прямой. Шаг 3

С другой стороны, если координаты х и у какой-нибудь точки удовлетворяют уравнению (I), то эта точка равноудалена от точек А1 и А2, а значит, принадлежит прямой m.
Таким образом, уравнение (I) является уравнением прямой m.
Преобразуем это уравнение:

Воспользуемся формулами сокращенного умножения, перегруппируем и перенесем все слагаемые в левую часть:

Введем обозначения:

Подставим новые обозначения в уравнение прямой. Получим:

По крайней мере одно из чисел a, b будет не равно нулю, так как точки А1 и А2 различны, и, следовательно, различны их координаты.
В силу произвольности выбранной точки А этому уравнению удовлетворяют координаты любой точки прямой m (если точка А(х, у) не принадлежит прямой m, то А1А≠А2А и координаты точки А не удовлетворяют полученному уравнению).
Уравнение прямой выведено.

Вывод уравнения прямой. Шаг 5

MATHVOX

Go to Top

Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять

Privacy & Cookies Policy

Источник: https://mathvox.ru/geometria/dekartovi-koordinati-uravneniya-figur-v-dekartovoi-sisteme-koordinat/glava-4-uravneniya-pryamoi/uravnenie-pryamoi-obschee-uravnenie-pryamoi/

Уравнение прямой – виды уравнения прямой: проходящее через точку, общее, каноническое, параметрическое и т.д

Уравнение прямой проходящей через точку и нормальный вектор

Рассмотрим уравнение прямой проходящей через точку и нормальный вектор. Пусть в системе координат задана точка и ненулевой вектор (рис. 1).

Рис. 1

Докажем, что линейное уравнение

(1)

это уравнение прямой , то есть координаты каждой точки прямой удовлетворяют уравнение (1), но координаты точки, что не лежит на , уравнения (1) не удовлетворяют.

(2)

Дальше используем очевидное свойство прямой : векторы и перпендикулярны тогда, и только тогда, когда точка лежит на . А при условии перпендикулярности обоих векторов их скалярное произведение (2) превращается в для всех точек , что лежат на , и только для них. Значит, (1) – уравнение прямой .

Общее уравнение прямой

Превратим уравнение (1)

+ + – = .

(3)

– общее уравнение прямой.

Таким образом, прямой линии отвечает линейное уравнение вида (3). Наоборот, за данным уравнением вида (3), где хотя бы один из коэффициентов и не равен нулю, можно построить прямую.

Действительно, пусть пара чисел удовлетворяют уравнение (3), то есть

Исследование общего уравнения прямой

Рис. 2
Считаем, что:
–>.

Если положить , тогда , получается ещё одна точка (см. рис. 2).

2. , тогда уравнение выглядит так , где = –. Нормальный вектор лежит на оси , прямая . Таким образом, прямая перпендикулярна в точке , либо же параллельна оси (см. рис. 3). В частности, если и , тогда и уравнение – это уравнение оси ординат.

Рис. 3

3. Аналогично, при уравнение записывается , где . Вектор принадлежит оси . Прямая в точке (рис. 4) .

Рис. 4
Если же , тогда уравнение оси .
Исследование можно сформулировать в такой форме: прямая параллельна той координатной оси, смена которой в общем уравнении прямой отсутствует.
Например:

1. прямая , слагаемое с отсутствует, поэтому .

2. прямая .

Уравнение прямой в отрезках

Построим прямую по общему уравнению при условии, что – не равны нулю. Для этого достаточно найти две точки, что лежат на этой прямой. Такие точки иногда удобнее находить на координатных осях.

Положим , тогда = –.

При , тогда = –.

Обозначим – = , – = . Найдены точки и . Отложим на осях и и через них проведём прямую (см. рис. 5).

Рис. 5
От общего можно перейти к уравнению, в которое будут входить числа и :
И тогда получается:
Либо, согласно обозначению, получим уравнение,
+ =
(4)

Которое называется уравнением прямой в отрезках. Числа и с точностью к знаку равняются отрезкам, которые отсекаются прямой на координатных осях.

Уравнение прямой с угловым коэффициентом

Чтобы узнать, что такое уравнение прямой с угловым коэффициентом, рассмотрим уравнение (1):
+ = – x
Обозначив – = , получим
=
(5)

уравнение прямой, которая проходит через точку в заданном направлении. Геометрическое содержание коэффициента понятно из рис. 6.

В = = , где – наименьший угол, на который нужно повернуть положительное направление оси вокруг общей точки до совмещения её с прямой . Очевидно, что если угол – острый, тогда ; если же – тупой угол, тогда .

Раскроем скобки в (5) и упростим его:
=
(6)

где . Соотношение (6) – уравнение прямой с угловым коэффициентом. При , – отрезок, который отсекает прямую на оси (см. рис. 6).

Обратите внимание! Для перехода от общего уравнения прямой к уравнению с угловым коэффициентом необходимо сначала решить относительно .

Рис. 6
= – x + – =

где обозначено = –, = –. Если же , тогда из исследования общего уравнения уже известно, что такая прямая перпендикулярна оси .

Каноническое уравнение прямой

Рассмотрим каноническое уравнение прямой при помощи примера.

Пусть в системе координат задана точка и ненулевой вектор (рис. 7).

Рис. 7

Необходимо составить уравнение прямой, что проходит через точку параллельно вектору , который называется направляющим вектором. Произвольная точка принадлежит этой прямой тогда и только тогда, когда . Так как вектор – задан, а вектор , тогда согласно условию параллельности, координаты этих векторов пропорциональны, то есть:

= .
(7)
Обратим внимание, что к уравнению вида (7) можно перейти, например, от уравнения пучка прямых (4)
= ,
или от уравнения прямой через точку и нормальный вектор (1):
=
Выше предполагалось, что направляющий вектор – ненулевой, но может так случиться, что одна из его координат, например, . Тогда выражение (7) формально запишется:
= ,

который, вообще не имеет смысла. Однако, принимают и получают уравнение прямой перпендикулярной оси . Действительно, из уравнения видно, что прямая определена точкой и направляющим вектором , перпендикулярным оси . Если в этом уравнении освободиться от знаменателя, тогда получим:

. , либо – уравнение прямой, перпендикулярной оси . Аналогично было бы получено для вектора .

Параметрическое уравнение прямой

Чтобы понять, что такое параметрическое уравнение прямой, необходимо вернуться к уравнению (7) и приравнять каждую дробь (7) до параметра . Так как хотя бы один из знаменателей в (7) не равен нулю, а соответствующий числитель может приобретать произвольные значения, тогда область смены параметра – вся числовая ось.

Получим:
= , =
или
(8)

Примеры задач на прямую линию

Конечно же, сложно что-либо решить исключительно по определениям, ведь нужно решить самостоятельно хотя бы несколько примеров или задач, которые помогут закрепить пройденный материал. Поэтому, давайте разберём основные задачи на прямую линию, так как похожие задачи часто попадаются на экзаменах и зачётах.

Каноническое и параметрическое уравнение

Пример 1На прямой линии заданной уравнением , найти точку , которые находятся от точки этой прямой на расстоянии 10 единиц.

Решение:

Пусть искомая точка прямой, тогда для расстояния запишем . При условии . Так как точка принадлежит прямой , у которой есть нормальный вектор , тогда уравнение прямой можно записать: = = и далее получается:

Тогда расстояние . При условии , или . Из параметрического уравнения:

Ответ: .

Пример 2

Задача

Точка движется равномерно со скоростью по направлению вектора от начальной точки . Найти координаты точки через от начала движения.

Решение
Сначала нужно найти единичный вектор . Его координаты – это направляющие косинусы:
= = ; = =
Тогда вектор скорости:
= x = x = .
Каноническое уравнение прямой теперь запишется:

= = , = – параметрическое уравнение. После этого нужно воспользоваться параметрическим уравнением прямой при .

Ответ

Угол между двумя прямыми

Пример

В равнобедренном прямоугольном треугольнике известна вершина прямого угла и уравнение гипотенузы . Составить уравнение катетов.

Решение:
Уравнение прямой, которая проходит через точку находим по формуле пучка прямых , где угловой коэффициент для прямой и = для прямой .
При условии , , поэтому и находим по формуле :
=
(9)

Учитывая рисунок, где видно, что между прямыми и – два угла: один острый , а второй – тупой . Согласно формуле (9) – это тот угол между прямыми и , на который нужно повернуть прямую против часовой стрелки относительно их точки пересечения до совмещения её с прямой .

Итак, формулу вспомнили, с углами разобрались и теперь можно вернуться к нашему примеру. Значит, учитывая формулу (9) находим сначала и уравнения катета .

Так как поворот прямой на угол против часовой стрелки относительно точки приводит к совмещению с прямой , тогда в формуле (9) , а . Из уравнения :
, поэтому
= Далее следует:
= = = = .
По формуле пучка уравнения прямой запишется:
= .
Аналогично находим , а ,
= Далее:
= = .
Уравнение прямой :
= .
Ответ: , .

Источник: https://NauchnieStati.ru/spravka/uravnenie-pryamoi/