Замечательные точки треугольника, формулы и примеры

• Тема: Повторение курса геометрии 8 класса
• Урок: Четыре замечательные точки треугольника
• Треугольник – это, прежде всего, три отрезка и три угла, поэтому свойства отрезков и углов являются основополагающими.

Задан отрезок АВ. У любого отрезка есть середина, и через нее можно провести перпендикуляр – обозначим его за р. Таким образом, р – серединный перпендикуляр.

1. Теорема (основное свойство серединного перпендикуляра)
2. Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
3. Доказать, что
4. Доказательство:

Рассмотрим треугольники  и  (см. Рис. 1). Они прямоугольные и равные, т.к. имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, то есть , что и требовалось доказать.

• Рис. 1
• Справедлива обратная теорема.
• Теорема
• Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.

Задан отрезок АВ, серединный перпендикуляр к нему р, точка М, равноудаленная от концов отрезка (см. Рис. 2).

Доказать, что точка М лежит на серединном перпендикуляре к отрезку.

Рис. 2

Доказательство:

Рассмотрим треугольник . Он равнобедренный, так как  по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана.

Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что . Но прямая р также перпендикулярна АВ.

Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит, прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.

Если необходимо описать окружность около одного отрезка, это можно сделать, и таких окружностей бесконечно много, но центр каждой из них будет лежать на серединном перпендикуляре к отрезку.

Говорят, что серединный перпендикуляр есть геометрическое место точек, равноудаленных от концов отрезка.

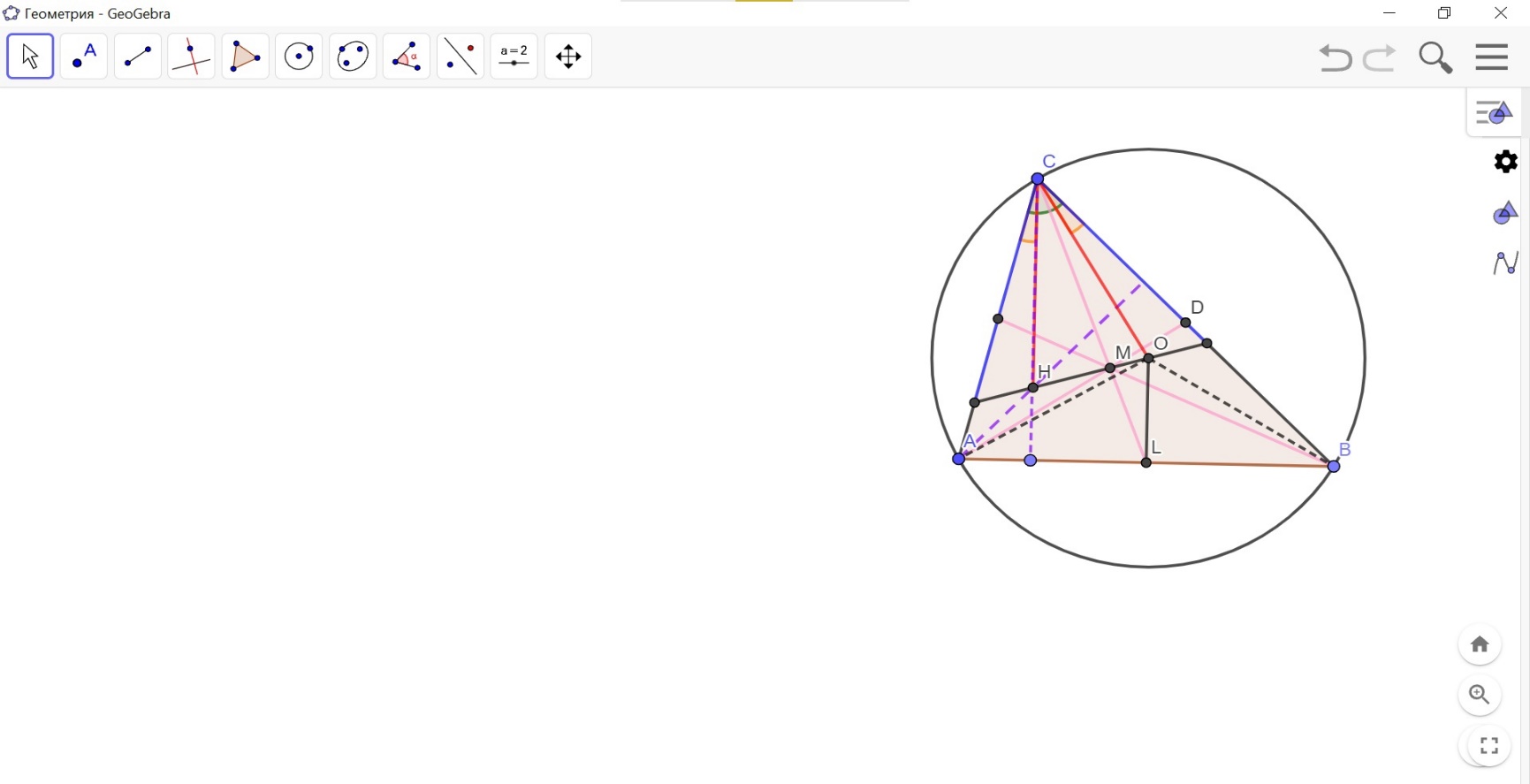
Треугольник состоит из трех отрезков. Проведем к двум из них серединные перпендикуляры и получим точку О их пересечения (см. Рис. 3).

Кроме того, точка О находится на серединном перпендикуляре к отрезку АВ, т.е. , вместе с тем , отсюда .

Таким образом, точка О пересечения двух серединных

1. Рис. 3
2. перпендикуляров треугольника равноудалена от его вершин, а значит, она лежит и на третьем серединном перпендикуляре.
3. Мы повторили доказательство важной теоремы.
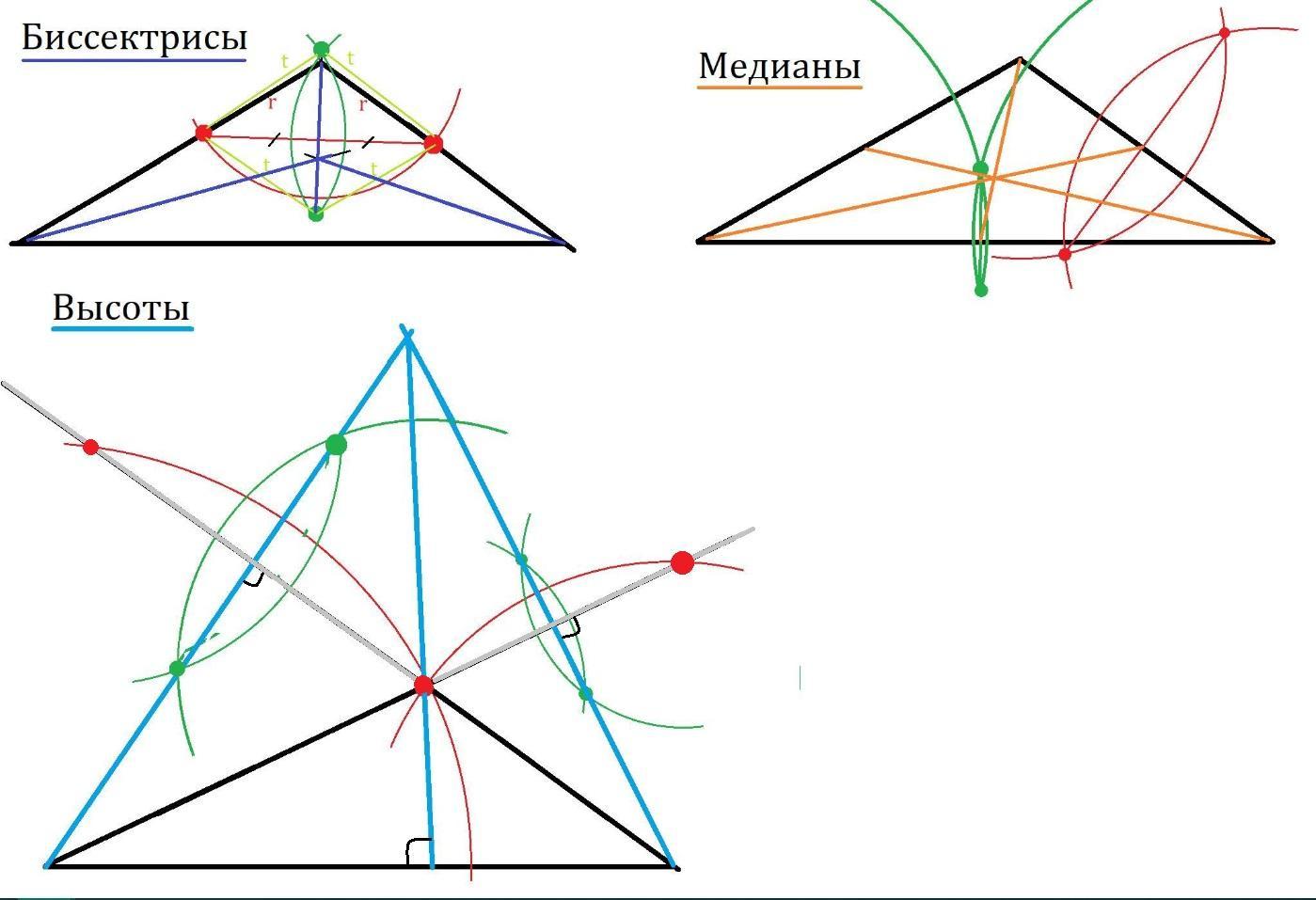
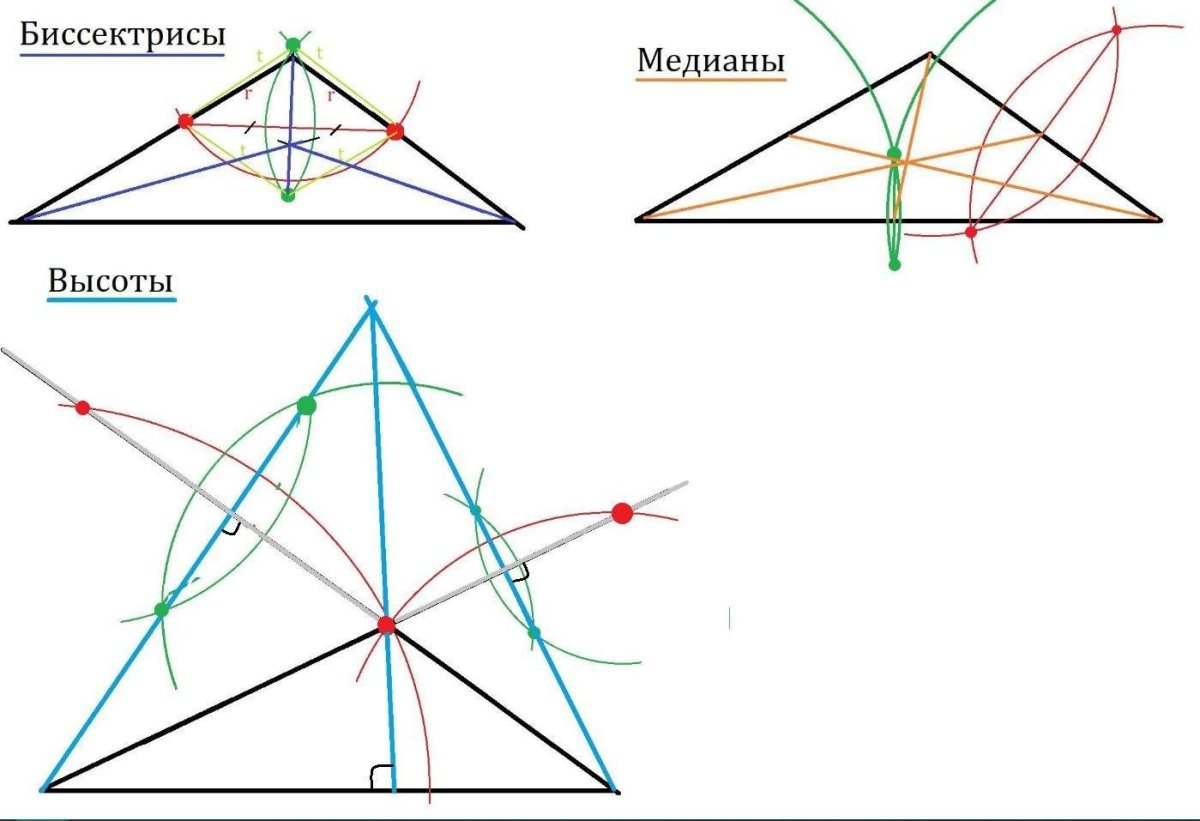
4. Три серединных перпендикуляра треугольника пересекаются в одной точке – центре описанной окружности.
5. Итак, мы рассмотрели первую замечательную точку треугольника – точку пересечения его серединных перпендикуляров.

Перейдем к свойству произвольного угла (см. Рис. 4).

Задан угол , его биссектриса AL, точка М лежит на биссектрисе.

• Рис. 4
• Если точка М лежит на биссектрисе угла, то она равноудалена от сторон угла, то есть расстояния от точки М до АС и до ВС сторон угла равны.
• Доказательство:

Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.

Рассмотрим треугольники  и . Это прямоугольные треугольники, и они равны, т.к. имеют общую гипотенузу АМ, а углы  и  равны, так как AL – биссектриса угла . Таким образом, прямоугольные треугольники равны по гипотенузе и острому углу, отсюда следует, что , что и требовалось доказать. Таким образом, точка на биссектрисе угла равноудалена от сторон этого угла.

Справедлива обратная теорема.

Теорема

Если точка равноудалена от сторон неразвернутого угла, то она лежит на его биссектрисе (см. Рис. 5).

Задан неразвернутый угол , точка М, такая, что расстояние от нее до сторон угла одинаковое.

Доказать, что точка М лежит на биссектрисе угла.

Рис. 5

Доказательство:

Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.

Если необходимо вписать в угол окружность, это можно сделать, и таких окружностей бесконечно много, но их центры лежат на биссектрисе данного угла.

Говорят, что биссектриса есть геометрическое место точек, равноудаленных от сторон угла.

Треугольник состоит из трех углов. Построим биссектрисы двух из них, получим точку О их пересечения (см. Рис. 6).

Точка О лежит на биссектрисе угла , значит, она равноудалена от его сторон АВ и ВС, обозначим расстояние за r: . Также точка О лежит на биссектрисе угла , значит, она равноудалена от его сторон АС и ВС: , , отсюда .

Несложно заметить, что точка пересечения биссектрис равноудалена от сторон третьего угла, а значит, она лежит на

Рис. 6

биссектрисе угла . Таким образом, все три биссектрисы треугольника пересекаются в одной точке.

1. Итак, мы вспомнили доказательство еще одной важной теоремы.
2. Биссектрисы углов треугольника пересекаются в одной точке – центре вписанной окружности.
3. Итак, мы рассмотрели вторую замечательную точку треугольника – точку пересечения биссектрис.
4. Мы рассмотрели биссектрису угла и отметили ее важные свойства: точки биссектрисы равноудалены от сторон угла, кроме того, отрезки касательных, проведенных к окружности из одной точки, равны.

Введем некоторые обозначения (см. Рис. 7).

Обозначим равные отрезки касательных через х, у и z. Сторона ВС, лежащая против вершины А, обозначается как а, аналогично АС как b, АВ как с.

Рис. 7

Задача 1: в треугольнике известны полупериметр и длина стороны а. Найти длину касательной, проведенной из вершины А – АК, обозначенную за х.

Очевидно, что треугольник задан не полностью, и таких треугольников много, но, оказывается, некоторые элементы у них общие.

Для задач, в которых речь идет о вписанной окружности, можно предложить следующую методику решения:

1.      Провести биссектрисы и получить центр вписанной окружности.

2.      Из центра О провести перпендикуляры к сторонам и получить точки касания.

3.      Отметить равные касательные.

4.      Выписать связь между сторонами треугольника и касательными.

5.      Решить систему в соответствии с требованиями задачи.

1. Согласно условию, нам необходимо найти только касательную х, для этого сложим все три уравнения системы:
2. В левой части уравнения мы получили периметр треугольника :
3. Сократим на два:
4. Получили важный факт: полупериметр есть сумма трех различных касательных.
5. , отсюда ,
6. Можно самостоятельно выразить аналогично отрезки касательных у через сторону b и z через сторону с:
7. Выразим одну из касательных только через стороны треугольника:
8. В прямоугольном треугольнике одна из касательных является радиусом:
9. Для доказательства данного факта рекомендуется пользоваться описанным выше алгоритмом.
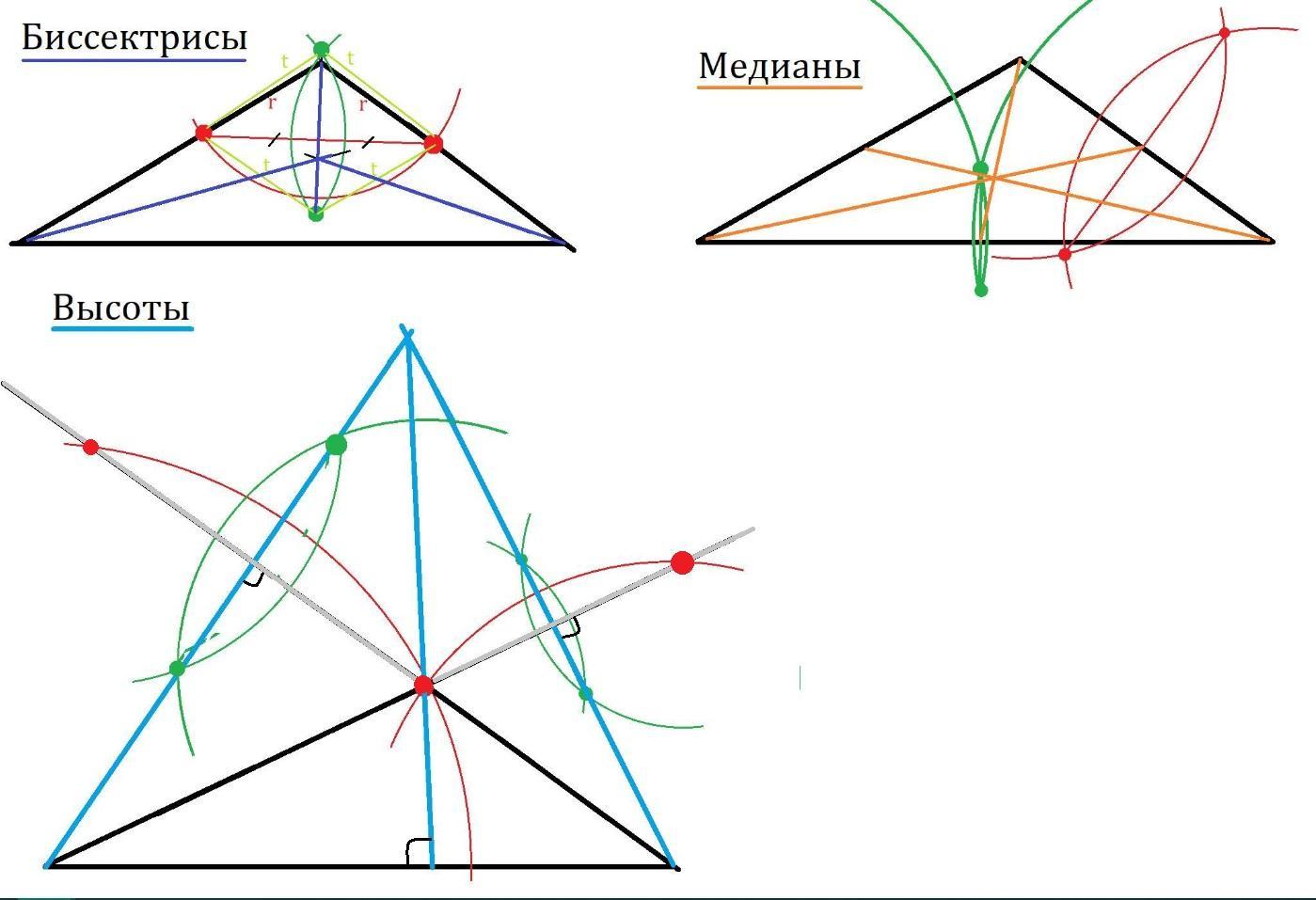
10. Третья замечательная точка треугольника – точка пересечения высот (или их продолжений) – ортоцентр.
11. Последняя замечательная точка – точка пересечения медиан.
12. Напомним, что три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
13. Итак, мы рассмотрели четыре замечательных точки треугольника, подробно вспомнили центр описанной и вписанной окружностей, доказали теоремы, кроме того, упомянули ортоцентр и точку пересечения медиан.
14. Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Bymath.net (Источник).
2. School-collection.edu.ru (Источник).

Домашнее задание

1. Задание 1: докажите, что в остроугольном треугольнике точка пересечения высот является центром окружности, вписанной в треугольник, вершинами которого являются основания высот данного треугольника.
2. Задание 2: докажите, что точка пересечения медиан треугольника, с вершинами в серединах сторон данного, совпадает с точкой пересечения медиан данного треугольника.
3. Задание 3: в треугольнике  угол  равен , Н – точка пересечения высот. Чему может быть равен угол ?

Источник: https://interneturok.ru/lesson/geometry/8-klass/povtorenie-kursa-geometrii-8-go-klassa/chetyre-zamechatelnye-tochki-treugolnika

Исследовательский проект Замечательные точки треугольника

• Содержание
• Введение………………………………………………………………………………………3
• Глава1. Исторические сведения о замечательных точках треугольника

1.1 Треугольник………………………………………………………………………………..4

1.2. Медианы треугольника

1.3. Биссектрисы треугольника

1.4. Высоты в треугольнике

1.5. Серединные перпендикуляры к сторонам треугольника

Глава 2. Исследование замечательных точек треугольника.

1. Заключение
2. Список использованной литературы
3. Буклет
4. Введение

Геометрия — это раздел математики, который рассматривает различные фигуры и их свойства. Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является символом геометрии; но он не только символ, треугольник — атом геометрии.

• В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан и высот треугольника, расскажу о замечательных их свойствах и линиях треугольника.
• К числу таких точек, изучаемых в школьном курсе геометрии, относятся:
• а) точка пересечения биссектрис (центр вписанной окружности);
• б) точка пересечения серединных перпендикуляров (центр описанной окружности);
• в) точка пересечения высот (ортоцентр);
• г) точка пересечения медиан (центроид).
• Актуальность: расширить свои знания о треугольнике,свойствах егозамечательных точек.
• Цель: исследование треугольника на его замечательные точки,изучение ихклассификаций и свойств.
• Задачи:
• 1. Изучить необходимую литературу
• 2. Изучить классификацию замечательных точек треугольника

3. Уметь строить замечательные точки треугольника.

4. Обобщить изученный материал для оформления буклета.

1. Гипотеза проекта:
2. умение находить замечательные точки в любом треугольнике, позволяет решать геометрические задачи на построение.
3. Глава 1. Исторические сведения о замечательных точках треугольника

 В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.

Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга.

В «Началах» не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос» означает «прямой», «правильный»). Это предложение было, однако, известно Архимеду, Паппу, Проклу.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер. В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера».

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки — вершины треугольника, отрезки — стороны треугольника.

• В А, В, С — вершины
• АВ, ВС, СА — стороны
• А С
• С каждым треугольником связаны четыре точки:

1. Точка пересечения медиан;

2. Точка пересечения биссектрис;

3. Точка пересечения высот.

4. Точка пересечения серединных перпендикуляров;

1.2. Медианы треугольника

Медина треугольника ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны (Рисунок 1). Точка пересечения медианы со стороной треугольника называется основанием медианы.

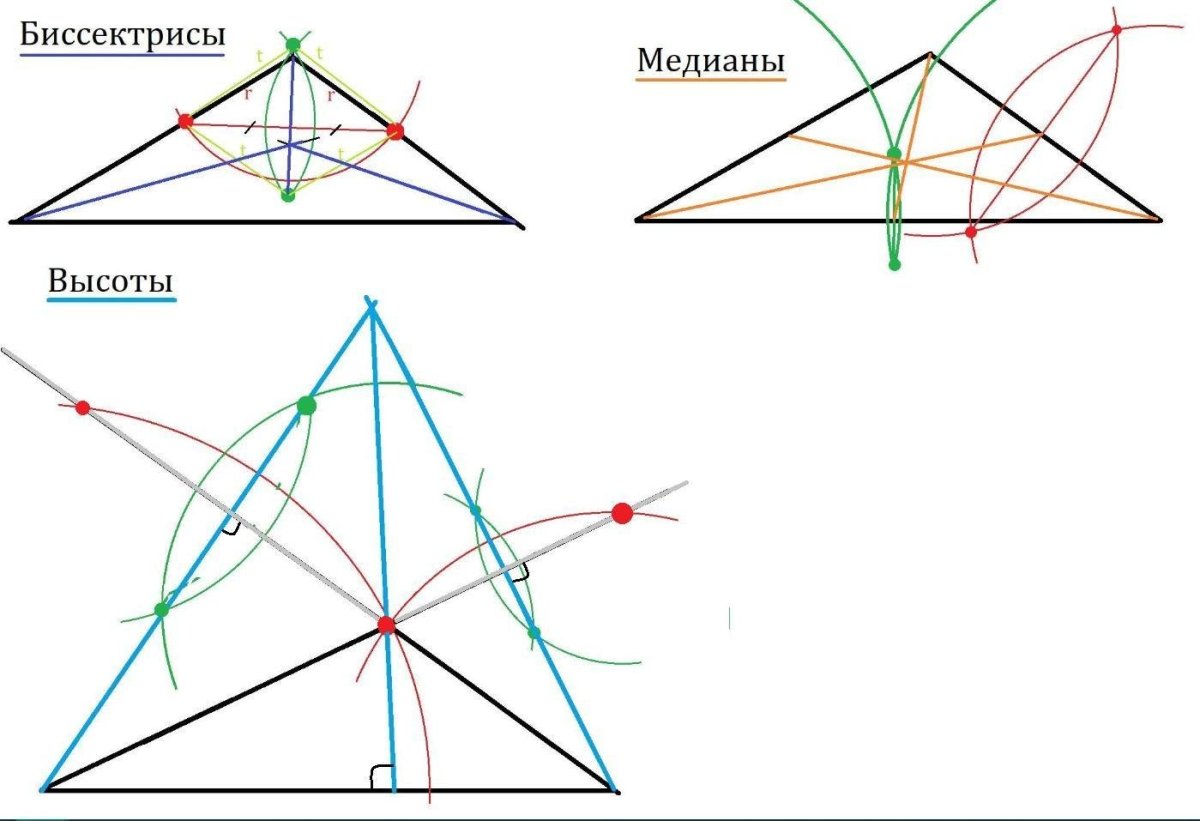
Рисунок 1. Медианы треугольника

Построим середины сторон треугольника и проведем отрезки, соединяющую каждую из вершин с серединой противолежащей стороны. Такие отрезки называются медианой.

И вновь мы наблюдаем, что и эти отрезки пересекаются в одной точке. Если мы измерим длины получившихся отрезков медиан, то можно проверить еще одно свойство: точка пересечения медиан делит все медианы в отношении 2:1, считая от вершин.

И еще, треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии! Точка, обладающая таким свойством, называется центром тяжести (барицентр). Центр равных масс иногда называют центроидом.

 Поэтому свойства медиан треугольника можно сформулировать так: медианы треугольника пересекаются в центре тяжести и точкой пересечения делятся в отношении 2:1, считая от вершины.

1.3. Биссектрисы треугольника

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам (Рисунок 2).

Рисунок 2. Биссектриса треугольника

В произвольном треугольнике ABC проведем биссектрисы его углов. И вновь при точном построении все три биссектрисы пересекутся в одной точке D. Точка D – тоже необычная: она равноудалена от всех трех сторон треугольника. В этом можно убедиться, если опустить перпендикуляры DA 1, DB 1 и DC1 на стороны треугольника. Все они равны между собой: DA1=DB1=DC1.

Если провести окружность с центром в точке D и радиусом DA 1, то она будет касаться всех трех сторон треугольника (то есть будет иметь с каждым из них только одну общую точку). Такая окружность называется вписанной в треугольник. Итак, биссектрисы углов треугольника пересекаются в центре вписанной окружности.

1.4. Высоты в треугольнике

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или прямую, совпадающую с противоположной стороной.

В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника (Рисунок 3).

Рисунок 3. Высоты в треугольниках

• Если в треугольнике построить три высоты, то все они пересекутся в одной точке H. Эта точка называется ортоцентром. (Рисунок 4).

С помощью построений можно проверить, что в зависимости от вида треугольника ортоцентр располагается по – разному:

• у остроугольного треугольника – внутри;
• у прямоугольного – на гипотенузе;
• у тупоугольного – снаружи.

Рисунок 4. Ортоцентр треугольника

Таким образом, мы познакомились еще с одной замечательной точкой треугольника и можем сказать, что: высоты треугольника пересекаются в ортоцентре.

1.5. Серединные перпендикуляры к сторонам треугольника

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

Начертим произвольный треугольник ABC и проведем серединные перпендикуляры к его сторонам. Если построение выполнено точно, то все перпендикуляры пересекутся в одной точке – точке О. Эта точка равноудалена от всех вершин треугольника. Другими словами, если провести окружность с центром в точке О, проходящую через одну из вершин треугольника, то она пройдет и через две другие его вершины.

Окружность, проходящая через все вершины треугольника, называется описанной около него. Поэтому установленное свойство треугольника можно сформулировать так: серединные перпендикуляры к сторонам треугольника пересекаются в центре описанной окружности (Рисунок 5).

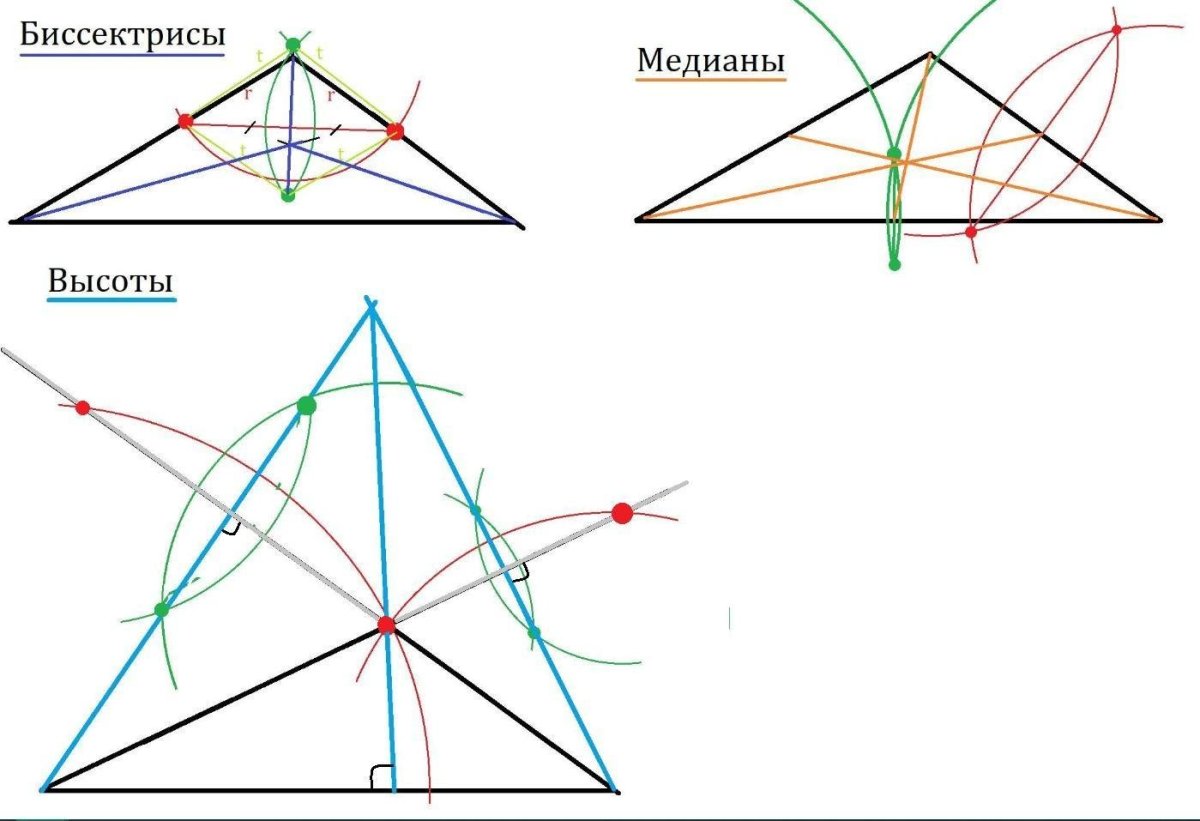Рисунок 5. Треугольник вписанный в окружность

Глава 2. Исследование замечательных точек треугольника.

Исследование высоты в треугольниках

 Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.

 Высоты остроугольного треугольника расположены строго внутри треугольника.

Соответственно, точка пересечения высот также находится внутри треугольника.

В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты, проведенные из вершин острых углов к катетам).

Высота, проведенная к гипотенузе, лежит внутри треугольника .

1. AC — высота, проведенная из вершины С к стороне AB.
2. AB — высота, проведенная из вершины B к стороне AC.
3. AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.
4. Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А — ортоцентр).
5. В тупоугольном треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.
6. Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.

• AK — высота, проведенная к стороне BC.
• BF — высота, проведенная к продолжению стороны АС.
• CD — высота, проведенная к продолжению стороны AB.
• Точка пересечения высот тупоугольного треугольника также находится вне треугольника:
• H — ортоцентр треугольника ABC.
• Исследование биссектрис в треугольнике
• Биссектриса треугольника является частью биссектрисы угла треугольника (луча), которая находится внутри треугольника.
• Все три биссектрисы треугольника пересекаются в одной точке.
• Точка пересечения биссектрис в остроугольном, тупоугольном и прямоугольном треугольниках, является центром вписанной в треугольник окружности и находится внутри.
• Исследование медиан в треугольнике
• Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три.

Исследовав эти треугольники я понял, что в любом треугольнике медианы пересекаются в одной точке. Эту точку называют центром тяжести треугольника.

1. Исследование серединных перпендикуляров к стороне треугольника
2. Серединный перпендикуляр треугольника – это перпендикуляр, проведенный к середине стороны треугольника.
3. Три серединных перпендикуляра треугольника пересекаются в одной точке, являются центром описанной окружности.
4. Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – на середине гипотенузы.
5. Заключение
6. В ходе проделанной работы мы приходим к следующим выводам:

1. Цель достигнута: исследовали треугольник и нашли его замечательные точки.

2. Поставленные задачи решены:

• 1). Изучили необходимую литературу;
• 2). Изучили классификацию замечательных точек треугольника;
• 3). Научились строить замечательные точки треугольника;

4). Обобщили изученный материал для оформления буклета.

Гипотеза, что умение находить замечательные точки треугольника, помогает в решении задач на построение подтвердилась.

В работе последовательно излагаются приемы построения замечательных точек треугольника, приведены исторические сведения о геометрических построениях.

Сведения из данной работы могут пригодиться на уроках геометрии в 7 классе. Буклет может стать справочником по геометрии по изложенной теме.

Список литературы

1. Учебник.  Л.С. Атанасян «Геометрия 7-9 классы Мнемозина,2015.

2. Википедияhttps://ru.wikipedia.org/wiki/Геометрия#/media/File:Euclid%27s_postulates.png

3. Портал Алые Паруса https://ru.wikipedia.org/wiki/Геометрия

4. Ведущий образовательный портал России http://cendomzn.ucoz.ru/index/0-15157

Источник: https://infourok.ru/issledovatelskiy-proekt-zamechatelnie-tochki-treugolnika-3158516.html

Замечательные точки треугольника — презентация, доклад, проект скачать

Слайд 1

Описание слайда:

Замечательные точки треугольника

Слайд 2

Описание слайда:

Оглавление Треугольник Из истории Элементы треугольника Центр тяжести треугольника Центр вписанной и описанной окружности Ортоцентр и изогональные точки Точка Лемуана Прямая Эйлера Окружность девяти точек Точка Ферма Точка Жергонна Точка Нагеля Точка Брокара Прямая Симпсона

Слайд 3

Описание слайда:

Треугольник Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – «землемерие» (от греческого «гео» – «земля» и «метрео» – «измеряю»).
                

Слайд 4

Описание слайда:

 Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником.

 Треугольник по праву считается простейшей из фигур: любая плоская, то есть простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником.

Слайд 5

Слайд 6

Описание слайда:

ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА         В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.

Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. И три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос» означает «прямой», «правильный»).

Это предложение было, однако, известно Архимеду, Паппу, Проклу.

Слайд 7

Описание слайда:

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника.
        На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер. Четвертой особенной точкой треугольника является точка пересечения медиан.

Архимед доказал, что она является центром тяжести (барицентром) треугольника.
        На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер.

Слайд 8

Описание слайда:

 В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера». В двадцатых годах XIX века французские математики Ж. Понселе, Ш.

Брианшон и другие установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же окружности.

       

Слайд 9

Описание слайда:

Эта окружность называется «окружностью девяти точек», или «окружностью Фейербаха», или «окружностью Эйлера». Фейербах установил, что центр этой окружности лежит на прямой Эйлера.
        Большой вклад в развитие геометрии треугольника внесли математики XIX – XX веков Лемуан, Брокар, Тебо и другие.

Эта окружность называется «окружностью девяти точек», или «окружностью Фейербаха», или «окружностью Эйлера». Фейербах установил, что центр этой окружности лежит на прямой Эйлера.
        Большой вклад в развитие геометрии треугольника внесли математики XIX – XX веков Лемуан, Брокар, Тебо и другие.

Слайд 10

Описание слайда:

      ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА       ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА Основными элементами треугольника ABC являются: вершины — точки A, B, и C; стороны — отрезки a = BC, b = AC и c = AB, соединяющие вершины; углы, образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, — буквами A, B и C.

Слайд 11

Описание слайда:

МЕДИАНА ТРЕУГОЛЬНИКА     Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Поэтому, для построения медианы необходимо выполнить следующие действия:
1) найти середину стороны;
2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Слайд 12

Описание слайда:

БИССЕКТРИСА ТРЕУГОЛЬНИКА Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.

Поэтому, для построения биссектрисы необходимо выполнить следующие действия:
1) построить биссектрису какого-либо угла треугольника (а биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса.

Слайд 13

Описание слайда:

ВЫСОТА ТРЕУГОЛЬНИКА Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.

Поэтому, для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведенной прямой, опустить перпендикуляр к ней (а перпендикуляр — это отрезок, проведенный из точки к прямой, составляющей с ней угол 90 градусов) — это и будет высота.

Слайд 14

Описание слайда:

СРЕДНИЕ ЛИНИИ ТРЕУГОЛЬНИКА Средние линии — это отрезки, соединяющие середины двух сторон.

Поэтому для построения средней линии необходимо выполнить следующие действия:
1) найти середины двух сторон треугольника;
2) соединить середины сторон отрезком — это и будет средняя линия.

Три средние линии треугольника образуют «вписанный» в него треугольник, называемый серединным. Его площадь в четыре раза меньше площади данного треугольника. А периметр в два раза меньше периметра данного треугольника.

Слайд 15

Описание слайда:

ЦЕНТР ТЯЖЕСТИ ТРЕУГОЛЬНИКА
( точка пересечения медиан) 1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношениии 2:1, начиная от вершины треугольника. 2. Медианы треугольника делят его на равновеликие треугольники.

Центр равных масс иногда называют центроидом. В этой же точке располагается и центр масс однородной треугольной пластинки. Если подобную пластинку поместить на булавку так, чтобы острие последней попало точно в центроид, то пластинка будет находиться в равновесии.

За особенности, описанные в пунктах 1-3, точку пересечения медиан и называют замечательной точкой треугольника.

Слайд 16

Описание слайда:

ЦЕНТР ВПИСАННОЙ ОКРУЖНОСТИ
(точка пересечения биссектрис) Биссектрисы любого треугольника пересекаются в одной точке, которая равноудалена от всех сторон треугольника, то есть является центром вписанной окружности.

Слайд 17

Описание слайда:

ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ
(точка пересечения серединных перпендикуляров)   Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром описанной окружности. Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника, в прямоугольном — на середине гипотенузы, а в тупоугольном — вне треугольника.

Слайд 18

Описание слайда:

ОРТОЦЕНТР ТРЕУГОЛЬНИКА
(точка пересечения высот) Высоты треугольника (или их продолжения) всегда пересекаются в одной точке, называемой его ортоцентром.
В остроугольгом треугольнике ортоцентр лежит внутри треугольника, в прямоугольном — совпадает с вершиной прямого угла, а в тупоугольном треугольнике — находится вне треугольника на пересечении продолжений высот.

Слайд 19

Описание слайда:

ИЗОГОНАЛЬНЫЕ ТОЧКИ Прямые, симметричные высотам относительно соответствующих биссектрис, проходят через центр описанной окружности, то есть содержат ее радиусы. Подобные две точки (синяя и оранжевая) называются изогональными. Таким образом, ортоцентр треугольника (синяя точка) изогонален центру описанной окружности (оранжевая точка)

Слайд 20

Описание слайда:

ТОЧКА ЛЕМУАНА Отразив относительно биссектрис треугольника соответствующие медианы, получаем новые замечательные линии — симедианы. Точка L их пересечения называется точкой Лемуана треугольника. Она является центроидом треугольника KMN, образованного ее проекциями на стороны исходного треугольника.

Слайд 21

Описание слайда:

Слайд 22

Описание слайда:

ОКРУЖНОСТЬ ДЕВЯТИ ТОЧЕК Середины сторон треугольника (точки A, B и С), основания его высот ( точки D, E и F) и середины отрезков от вершин до ортоцентра (точки M, K и H) лежат на одной окружности.

Ее радиус равен половине радиуса описанной окружности (отрезок NL), а центр О лежит посередине отрезка NS, где N — центр описанной окружности, а точка S — ортоцентр треугольника.

Такая окружность называется окружностью девяти точек, или окружностью Эйлера, или окружностью Фейербаха — по имени Карла Фейербаха, провинциального учителя математики из Германии, родного брата философа Людовика Фейербаха.

Слайд 23

Описание слайда:

ТОЧКА ФЕРМА Точка F — точка Ферма, то есть точка, сумма расстояний от которой до всех вершин треугольника ABC минимальна

Слайд 24

Описание слайда:

ТОЧКА ЖЕРГОННА Три отрезка, соединяющие вершины треугольника с точками, в которых вписанная в него окружность касается соответственно противоположных вершинам сторон, пересекаются в одной точке J. Она называется точкой Жергонна.

Слайд 25

Описание слайда:

ТОЧКА НАГЕЛЯ Отрезки, соединяющие каждую из вершин треугольника с точкой, в которой противоположная сторона касается соответствующей вневписанной окружности, пересекаются в одной точке N – точке Нагеля. Она интересна тем, что отрезок NI, где I – центр вписанной окружности, проходит через центр тяжести M (точка пересечения медиан) треугольника и делится им в отношении NM : MI = 2 : 1.

Слайд 26

Описание слайда:

ТОЧКА БРОКАРА Если на сторонах треугольника АВС внешним образом построить подобные ему треугольники СА1В, САВ1 и С1АВ (углы при первых вершинах всех четырех треугольников равны и т.д.), то прямые АА1, ВВ1 и СС1 пересекутся в точке Р, которую называют точкой Брокара. Одна из особеностей этой точки состоит в том, что РАС = РСВ = РВА.

Слайд 27

Описание слайда:

Источник: https://mypresentation.ru/presentation/1568846712_zamechatelnye-tochki-treugolnika

Видеоурок «Четыре замечательные точки треугольника»

Содержание:

§ 1  Теорема о биссектрисе угла

• С любым треугольником в геометрии связаны четыре точки:
• 1) точка пересечения медиан;
• 2) точка пересечения биссектрис;
• 3) точка пересечения высот (или их продолжений);
• 4) точка пересечения серединных перпендикуляров к сторонам.

1. Эти четыре точки называют замечательными точками треугольника.
2. В этом уроке рассмотрим и докажем теоремы, следствия из этих теорем, связанные с замечательными точками треугольника, и рассмотрим их применение при решении задач.
3. Познакомимся сначала с теоремой о биссектрисе угла.
4. Теорема:
5. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
6. Обратно:
7. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
8. Докажем эти утверждения.
9. Дано:
10. ∠ВАС, АМ – биссектриса, МК и МL перпендикулярны к прямым АВ и АС.
11. Доказать:
12. МК = МL
13. Доказательство:

• Рассмотрим прямоугольные треугольники АКМ и АLМ.
• Они равны по гипотенузе и острому углу (АМ – общая сторона, ∠1 = ∠2 , так как по условию АМ – биссектриса).
• Из равенства треугольников следует МК = МL.
• Теперь докажем обратное утверждение.
• Дано:
• ∠ВАС, точка М лежит внутри угла и равноудалена от сторон угла АВ и АС.
• Доказать:
• луч АМ – биссектриса ∠ВАС.
• Доказательство:

1. Проведем перпендикуляры МК и МL к прямым АВ и АС.
2. Прямоугольные треугольники АМК и АМL равны по гипотенузе и катету (АМ – общая гипотенуза, МК = МL по условию).
3. Следовательно, ∠1 = ∠2, это означает, что луч АМ – биссектриса ∠ВАС.
4. Теорема доказана.
5. Из утверждения теоремы следует еще одно утверждение.
6. Следствие: биссектрисы треугольника пересекаются в одной точке.

§ 2  Теорема о серединном перпендикуляре к отрезку

• Перейдем к теореме о серединном перпендикуляре к отрезку.
• Но сначала дадим определение.
• Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

1. На рисунке прямая а является серединным перпендикуляром к отрезку АВ.
2. Теорема:
3. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
4. Обратно:
5. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
6. Дано:
7. АВ – отрезок, прямая m – серединный перпендикуляр к отрезку АВ, точка О – середина этого отрезка.
8. М – произвольная точка прямой m.
9. Доказать: АМ = ВМ
10. Доказательство:
11. Если точка М совпадает с точкой О, то равенство АМ = ВМ верно.

• Пусть М и О – различные точки.
• Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ по условию, ОМ – общий катет), из равенства треугольников следует, что АМ = ВМ.
• Докажем обратное утверждение.
• Дано:
• АВ – отрезок, N – произвольная точка такая, что АN = ВN.
• Доказать:
• точка N лежит на прямой m – серединном перпендикуляре к АВ.
• Доказательство:
• если точка N – точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой m.

Если же точка N не лежит на прямой АВ, то треугольник АNВ – равнобедренный, так как АN = ВN.

Отрезок NО является медианой равнобедренного треугольника, значит, она является и его высотой.

Таким образом, NО перпендикулярен АВ, поэтому прямые ОN и m совпадают, т.е. точка N – точка прямой m.

1. Теорема доказана.
2. Следствием доказанной теоремы является следующее утверждение.
3. Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

§ 3  Теорема о пересечении высот теугольника

• Рассмотрим еще одну теорему о пересечении высот треугольника.
• Теорема:
• Высоты треугольника (или их продолжения) пересекаются в одной точке.
• Дано:
• АА1 , ВВ1, СС1 – высоты треугольника АВС.
• Доказать:
• АА1 , ВВ1, СС1 пересекаются в точке О.
• Доказательство:

1. Проведем через вершины А, В и С прямые, параллельные противоположным сторонам треугольника.
2. Получим треугольник А2В2С2.
3. Точки А, В, С являются серединами треугольника А2В2С2.

Действительно, в параллелограммах АВА2Си АВСВ2 противоположные стороны равны, т.е. АВ = А2С, АВ = СВ2 , поэтому А2С = СВ2.

• Аналогично С2А = АВ2 и С2В = ВА2.
• Из построения следует, что СС2 перпендикулярно А2В2, АА1 перпендикулярно В2С2, ВВ1 перпендикулярно А2С2.
• Таким образом, прямые АА1, ВВ1, СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2, следовательно, они пересекаются в одной точке.
• Теорема доказана.
• Решим задачу, используя полученные знания.
• Задача.
• В треугольнике АВС проведены высоты АК и ВD, пересекающиеся в точке О.
• Угол САВ = 42°.
• Найдите величину угла АСО.
• Дано:
• ∆АВС, АК и ВD – высоты треугольника АВС, пересекающиеся в точке О, ∠САВ = 42°
• Найти:
• ∠АСО.
• Решение:

1. для вычисления угла АСО проведем еще одну высоту СМ треугольника АВС, по теореме о пересечении высот треугольника высота СМ пройдет через точку О, а значит, треугольник АСМ – прямоугольный.
2. Тогда ∠АСО = 180° – (90° + 42°) = 48°.
3. В этом уроке познакомились с замечательными точками треугольника, рассмотрели теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку и их следствия, теорему о пересечении высот (или их продолжений), а также рассмотрели решение задачи по теме урока.

Список использованной литературы:

1. Л.С. Атанасян. Учебник. 8 класс.
2. Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва: «Вако», 2005.
3. Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
4. Д.А. Мальцева. Математика. 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
5. О.В. Белицкая. Геометрия. 8 класс. Тесты. – Саратов: «Лицей», 2009.
6. С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.

Источник: https://znaika.ru/catalog/8-klass/geometry/Chetyre-zamechatelnye-tochki-treugolnika.html

Замечательные линии треугольника

Медиана треугольника – это отрезок, который связывает вершину треугольника с серединой одной из сторон данного треугольника.

Медиана треугольника

Медиана делит треугольник на два треугольника, площади которых одинаковы.

Медианы треугольника пересекаются только в одной точке, которая разделяет каждую из них в отношении 2 : 1, отсчитывая от вершины. Такая точка именуется центром тяжести треугольника.

Весь треугольник разбивается своими медианами на шесть равных по значению треугольников.

Биссектриса угла – это исходящий из вершины угла луч, пролегающий между образующими сторонами и разделяющий его пополам.

Свойства биссектрисы треугольника

• Биссектриса угла – есть геометрическое место точек, которые равноудалены от сторон этого угла.
• Биссектриса угла треугольника, разделяет противолежащую сторону на отдельные отрезки, которые пропорциональны прилежащим сторонам:
• В точке, где пересекаются биссектрисы треугольника, находится центр окружности, который вписан в этот треугольник.

Высотой треугольника называется линия, проведенная из вершины треугольника к одной из сторон расположенной перпендикулярно.

Свойства высоты треугольника

Перпендикулярная линия высоты прямоугольного треугольника разделяет его на два подобных ему треугольника.

Две линии высоты остроугольного треугольника, отделяют от него подобные треугольники.

Перпендикулярная прямая, которая проходит через середину отрезка, называется – срединный перпендикуляр к отрезку.

Срединный перпендикуляр

Все точки серединного перпендикуляра к отрезку равноудалены от окончаний этого отрезка. Верно так же и обратное утверждение, что каждая точка, находящаяся на равных расстояниях от концов отрезка, расположена на серединном перпендикуляре к нему.

В точке пересечения серединных перпендикуляров, проведенных в направлении к одной из сторон треугольника, находится центр окружности, который описывает данный треугольник.

Отрезок, который соединяет две стороны треугольника в их серединах, называется – средняя линия треугольника.

Средняя линия

Средняя линия, какого либо треугольника, всегда расположена параллельно одной из его сторон и является половиной этой стороны.

Источник: http://simple-math.ru/geometry/line-triangle.php

Презентация на тему: Четыре замечательные точки треугольника

Описание слайда:

Четыре замечательные точки треугольника

Описание слайда:

Свойство биссектрисы неразвёрнутого угла Теорема1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Теорема 2 ( обратная).

Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.

Обобщённая теорема: биссектриса неразвёрнутого угла – множество точек плоскости, равноудалённых от сторон этого угла. Дано: ВАС, АХ – биссектриса, М є АХ, МЕ АВ, МК АС

Описание слайда:

Серединный перпендикуляр к отрезку Теорема 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. Дано: АВ – отрезок, РК – серединный перпендикуляр,М є РК Теорема 2. Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. Обобщённая теорема: серединный перпендикуляр к отрезку – множество точек плоскости, равноудалённых от его концов.

Описание слайда:

Первая замечательная точка треугольника Теорема. Биссектрисы треугольника пересекаются в одной точке.

Дано: АВС, АЕ, ВТ – биссектрисы, О — точка их пересечения Доказать: СУ – биссектриса АВС, О є СУ АЕ – биссектриса и ОМ АВ, ОК АС,значит, ОМ = ОК ВТ – биссектриса, и ОМ АВ, ОР ВС, значит, ОМ = ОP Значит, ОМ = ОК = ОР и ОР ВС, ОК АС, следовательно, О лежит на биссектрисе угла АСВ, т. е. СУ – биссектриса АВС. Значит, О – точка пересечения трёх биссектрис треугольника.

Описание слайда:

Вторая замечательная точка треугольника Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Дано: АВС, k,n – серединные перпендикуляры к сторонам треугольника, О – точка их пересечения Доказать: р – серединный перпендикуляр к ВС, О є р k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ.

Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном перпендикуляре к стороне ВС, т. е. на р.

Описание слайда:

Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:

Описание слайда:

Третья замечательная точка треугольника Теорема. Медианы треугольника пересекаются в одной точке, которая делит каждую в отношении 2: 1, считая от вершины. (центр тяжести треугольника – центроид) Дано: АВС, AM,ВК,СР — медианы Доказать: АМ ВК СР = О Доказательство проведено ранее: задача 1 п. 62.

Описание слайда:

Описание слайда:

Доказательство: Через вершины В, А, С треугольника АВС проведём ЕТ АС, ЕУ ВС, ТУ АВ. Получим: АСВЕ – параллелограмм, значит, АС = ВЕ АСТВ – параллелограмм, значит, АС = ВТ Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ. Т.к.

ВН – высота АВС по условию, то ВН АС Получим: ВН – серединный перпендикуляр к ЕТ. Аналогично, СМ – серединный перпендикуляр к ТУи АК — серединный перпендикуляр к УЕ. Т. е.

ВН, СМ, АК – серединные перпендикуляры к сторонам ЕТУ, которые по ранее доказанному пересекаются в одной точке,значит, высоты АВС пересекаются в одной точке.

Описание слайда:

Дано: АВС, АМ = ВМ, МD AB, AK = KC, DK AC, D є BC. Доказать: D — середина ВС, А = В + С. D є BC по условию, значит, ВD = AD AK = KC, DK AC, D є BC по условию, значит, AD = DC следовательно, D – середина ВС. б) По доказанному AD = DC, значит, треугольники АВD и АСD – равнобедренные, поэтому 1 = В, 2 = С. ВАС = 1 + 2 = В + С, что и т. д.

Источник: https://ppt4web.ru/geometrija/chetyre-zamechatelnye-tochki-treugolnika1.html