Формула индукции

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах.

Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри.

Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Вам это будет интересно  Обозначение нулевого защитного проводника

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Вам это будет интересно  Все об удельном сопротивлении

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Вам это будет интересно  Особенности резонанса токов

Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.

После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:

• X — индуктивное сопротивление;
• π — математическая постоянная (примерно 3,14);
• F — частота в герцах, при которой проводились измерения.

Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.

Источник: https://rusenergetics.ru/ustroistvo/induktivnost-katushki

Формула индукции

В этом разделе мы рассмотрим только три вида индукции: электромагнитную индукцию, индукцию магнитного поля и электрическую индукцию и основные формулы, при помощи которых данные виды индукции вычисляют.

Формула индукции электрического поля

• Электрическая индукция (или вектор электрического смещения ()) – это одна из основных векторных характеристик электрического поля. Формулой определяющей вектор электрической индукции является выражение:
•    
• где – вектор напряженности электрического поля; – вектор поляризации; – электрическая постоянная.
• Для изотропного вещества индукция электрического поля связана с напряженность это поля как:
•    
• где – диэлектрическая проницаемость вещества.
• Самой распространённой формулой, при помощи которой находят величину вектора индукции электростатического поля, является теорема Остроградского – Гаусса:
•    

Поток () вектора электростатической индукции () в диэлектрике через произвольную замкнутую поверхность равен сумме свободных зарядов, которые находятся внутри рассматриваемой поверхности. В данной форме теорема Гаусса выполняется и для однородной и изотропной среды, так и для неоднородной анизотропной.

Формула вектора индукции магнитного поля

1. Модуль вектора равен частному от деления максимальной силы Ампера (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
2.    
3. На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора :
4.    

где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.

• Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
•    
• где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
• Основными законами, которыми пользуются чаще всего для расчета магнитных полей, являются: закон Био-Савара-Лапласа и теорема о циркуляции вектора магнитной индукции.

Формула электромагнитной индукции

Если проводник помещен в переменное магнитное поле, то в нем возникает электродвижущая сила – это сущность явления электромагнитной индукции.

Основной закон электромагнитной индукции состоит в следующем: ЭДС электромагнитной индукции () в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока (), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.

В системе международных единиц (СИ) закон электромагнитной индукции записывают так:

   

где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф).

Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура () и направление его обода связаны.

Вектор должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки.

Примеры решения задач по теме «Индукция»

Понравился сайт? Расскажи друзьям!

Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-indukcii/

Самоиндукция простыми словами: определение, формулы, примеры

Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.

Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.

Определение

Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.

Рис. 1. Магнитное поле катушки

Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.

Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.

Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.

Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.

Рис. 2. Явление самоиндукции

Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.

Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).

Рис. 3. Схема опыта с лампочками

Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.

На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.

График на рисунке 4 красноречиво объясняет эффект задержки.

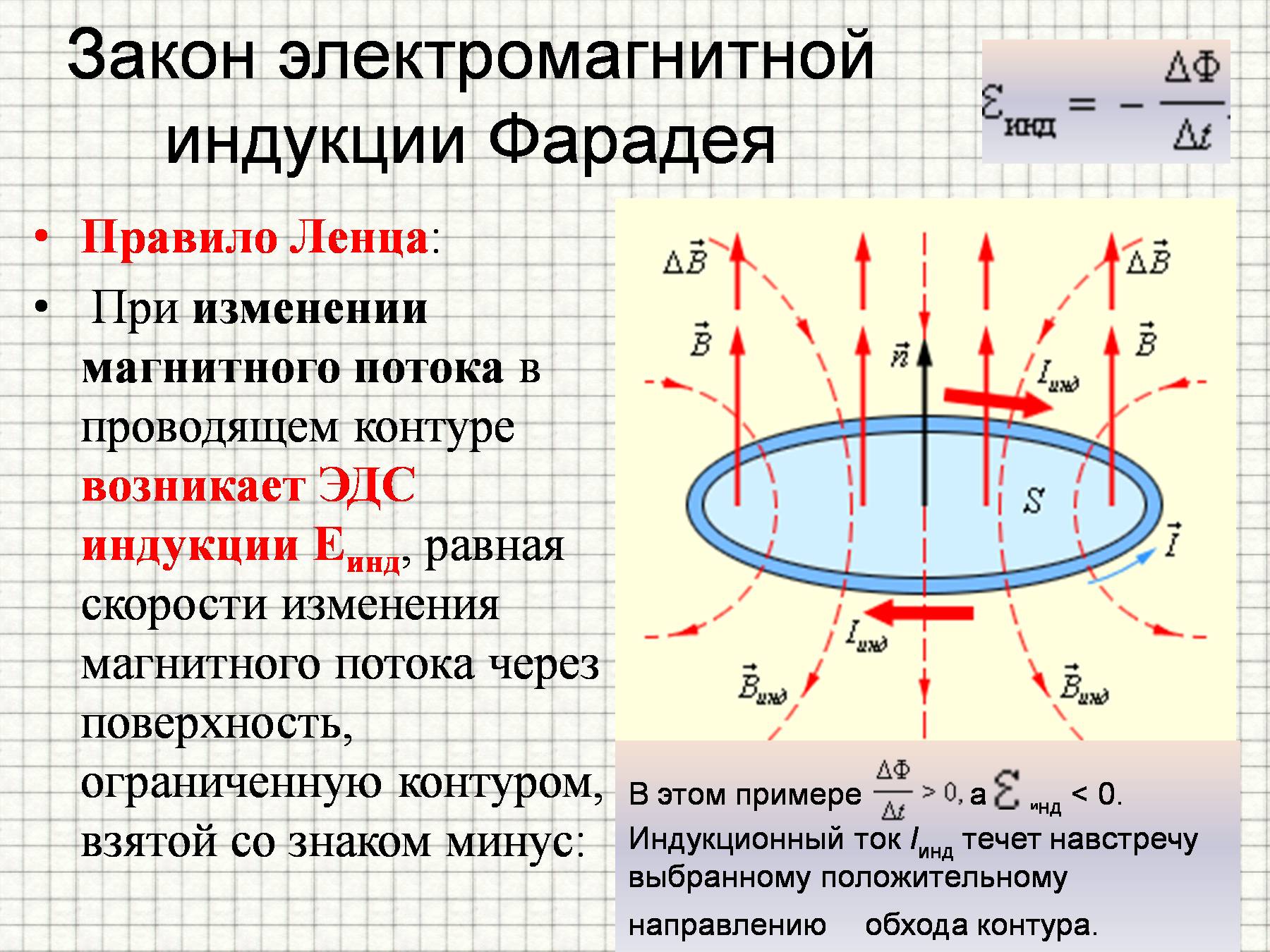Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности

Обратите внимание на нелинейность изменения силы тока по времени.

Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.

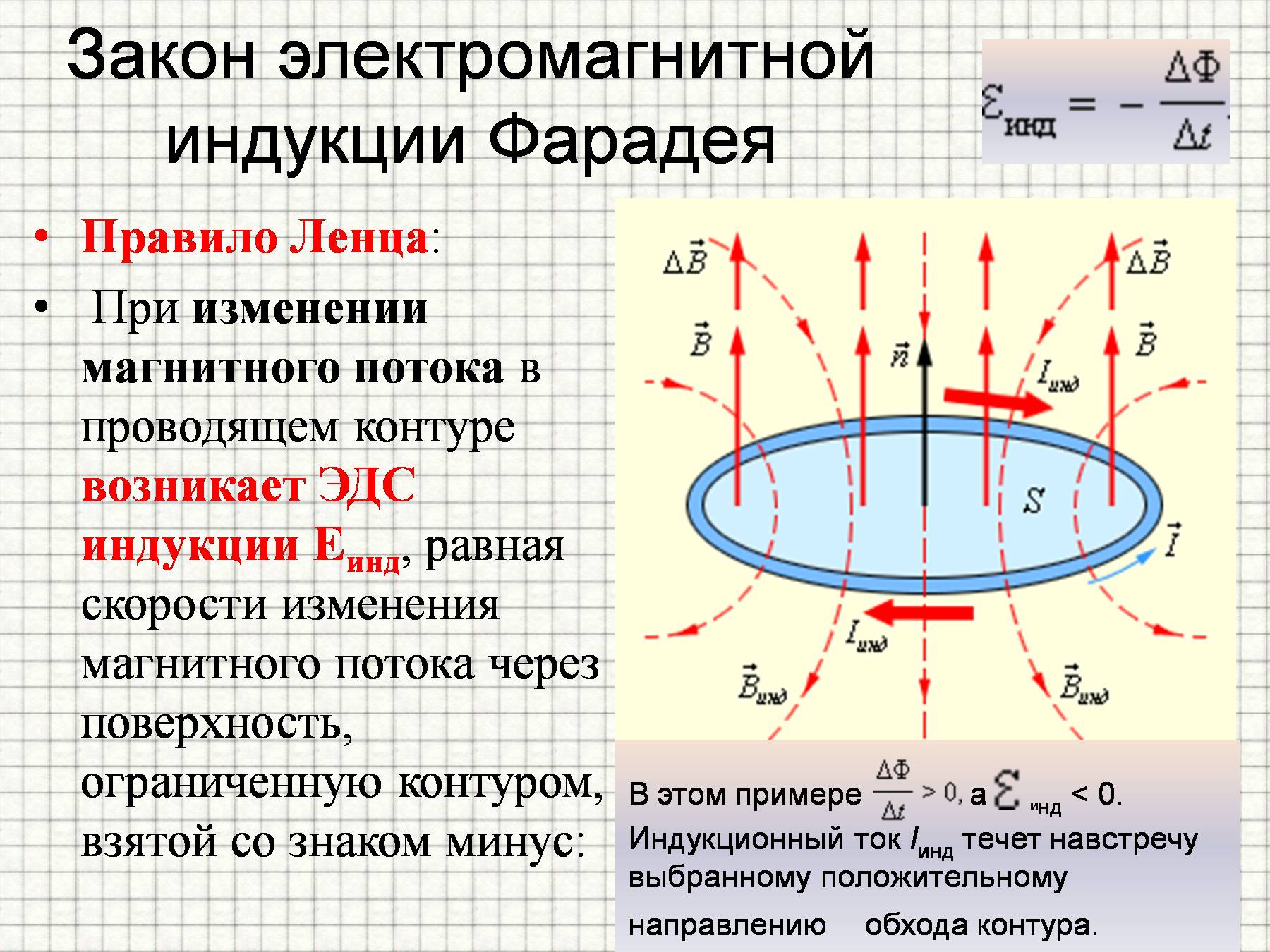Рис. 5. Возникновение самоиндукции

Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.

В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.

Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.

Формулы

Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.

При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.

Индуктивность

Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.

Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.

Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.

Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.

Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.

Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.

Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

1. На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
2. Электрическая цепь резко обрывается специальным прерывателем.
3. Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
4. Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

• шумы:
• пульсации;
• нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред.

При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п.

С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.

Видео в помощь

Источник: https://www.asutpp.ru/samoinduktsiya.html

Магнитная индукция. Определение и описание явления

Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.

Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.

Физический смысл магнитной индукции

Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.

Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.

 В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.

Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.

Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.

Формула магнитной индукции

• где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
• 
• 

Магнитный поток

1. Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур. 
2. Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.

    

3. Магнитометры, используемые для ее измерения, называют теслометрами.

Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).

После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

Источник: https://pue8.ru/elektrotekhnik/597-magnitnaya-induktsiya-opredelenie-i-opisanie-yavleniya.html

Электромагнитная индукция. — Закон электромагнитной индукции

Электромагнитная
индукция —
явление возникновения электрического
тока в
замкнутом контуре при изменении
магнитного
потока,
проходящего через него.

Электромагнитная
индукция была открыта Майклом
Фарадеем 29
августа 1831 года.

Он обнаружил, что
электродвижущая сила, возникающая в
замкнутом проводящем контуре,
пропорциональна скорости изменения
магнитного
поток через
поверхность, ограниченную этим контуром.

Величина электродвижущей
силы (ЭДС)
не зависит от того, что является причиной
изменения потока — изменение самого
магнитного поля или движение контура
(или его части) в магнитном поле. Электрический ток,
вызванный этой ЭДС, называется индукционным
током.

Зако́н
электромагни́тной инду́кции
Фараде́я является
основным законом электродинамики,
касающимся принципов
работы трансформаторов,дросселей,
многих видов электродвигателей и генераторов. Закон
гласит:

• Для
  любого замкнутого контура
  индуцированная электродвижущая
  сила (ЭДС) равна скорости
  изменения магнитного потока,
  проходящего через этот контур.

или
другими словами:

• Генерируемая
  ЭДС пропорциональна скорости изменения
  магнитного потока.

Согласно закону электромагнитной индукции Фарадея: 

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,  — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила, — число витков, — магнитный поток через один виток, — потокосцепление катушки.Информация взята с http://ru.wikipedia.org/wiki/Закон_электромагнитной_индукции_

Источник: https://www.sites.google.com/site/zakonelektromagnitnojindukcii/home/zakon-elektromagnitnoj-indukcii

Индуктивность: формула

Если существует замкнутый контур, в котором протекает ток, создающий магнитное поле (магнитный поток), то между током и потоком существует взаимосвязь. Коэффициент пропорциональностями между этими величинами является определением индуктивности.

Также эту пропорциональность можно назвать характеристикой инерционности электрической цепи, которая напрямую связана с понятием ЭДС самоиндукции, которая возникает в цепи, когда изменяется сила тока.

Электрическая цепь и индуктивность

Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.

Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.

Самоиндукция и измерение индуктивности

Расчет катушки индуктивности

При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.

• Напряжение ЭДС определяется формулой расчета индукции:
• Ꜫ=-L∙di/dt.
• То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».

Обозначение и единицы измерения

Сопротивление тока: формула

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

• В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
• В системе СГСЭ – в статгенри.

Теоретическое обоснование

Ток, протекающий в замкнутом контуре, создает магнитное поле, при этом величина вектора магнитного поля пропорциональна протекающему току. Таким образом, магнитный поток также пропорционален току.

Коэффициент пропорциональности между магнитным потоком и порождающим его током равен индуктивности рассматриваемого контура.

Свойства

Имеет следующие свойства:

• Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
• Не может быть отрицательной;
• Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
• При увеличении частоты тока реактивное сопротивление катушки увеличивается;
• Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.

Схемы соединения катушек

Как радиотехнический элемент, катушки индуктивностей обладают свойствами соединений, полностью идентичными соединениям резисторов.

Параллельное соединение

1. Параллельное соединение:
2. L=1/(1/L1+1/L2+…+1/Ln).
3. Для двух элементов формула упрощается:
4. L=L1∙L2/(L1+L2).

Последовательное соединение

Общее значение последовательного соединения равняется сумме индуктивностей:

L=L1+L2+…+Ln.

Добротность катушки

Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.

• Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:
• Q=2∙π∙f∙L/R,
• где:

• π – число пи, ≈3,14,
• f – частота,
• R – сопротивление.

Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает.

Одновитковой контур и катушка

1. Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
2. L=Ф/I.
3. Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
4. Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
5. L=L1∙N2.
6. Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

• Длина обмотки превышает диаметр в несколько раз;
• Толщина обмотки меньше диаметра катушки также в несколько раз.

Соленоидальный тип катушки

• Параметры соленоида можно узнать из такого выражения:
• L=µ0N2S/l,
• где:

• µ0 – магнитная постоянная;
• N – количество витков;
• S – площадь поперечного сечения обмотки;
• l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника.

Обратите внимание! Используя подвижный сердечник, можно производить оперативное изменение параметров соленоида.

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Тороидальная катушка (катушка с кольцевым сердечником)

1. Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:
2. L=µ∙µ0N2S/(2π∙r),
3. где r – усредненный радиус тороидального сердечника.
4. Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:
5. L=µ∙µ0N2S∙h/(2π)∙ln(R/r),
6. где:
7. r – внутренний радиус сердечника;
8. R – внешний радиус;
9. h – высота.

Важно! Вторая формула позволяет узнавать результат с большей точностью.

Длинный прямой проводник

• Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:
• L=µ0/(2π)∙l(µeln(l/r+1/4µi),
• где:

• µe и µi – магнитная проницаемость среды и материала проводника, соответственно;
• l и r – длина и радиус проводника.

Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.

Применение катушек индуктивности

Рассматриваемые элементы широко применяются в радио,- и электротехники:

• Частотозадающие цепи;
• Трансформаторы;
• Дроссели;
• Антенны;
• Элементы фильтров;
• Накопители энергии;
• Нагревательные элементы (система индукционного нагрева);
• Электромагниты;
• Датчики магнитного поля.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Последовательный и параллельный колебательные контуры

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Q-метр для измерения добротности

Видео

Источник: https://amperof.ru/teoriya/induktivnost-formula.html

Индуктивность: формула

Главная > Теория > Индуктивность: формула

Одним из основных и важных элементов, используемых в радиотехнике, является катушка индуктивности. Эта наиболее распространенная деталь радиоаппаратуры характеризуется рядом специфических и неповторимых физических свойств, без понимания которых невозможно полноценно осознавать процессы, происходящие в цепях.

Ориентация индукционных трасс поля

Понятия: индукция и индуктивность

В 1820 году датским ученым Хансом Эрстедом была найдена зависимость магнитного поля от тока: при протекании электрического тока по проводу вокруг него образовывается магнитное поле. С целью охарактеризовать магнитное поле был введен некий критерий – это магнитная индукция.

Поскольку магнитная индукция имеет свою ориентацию, то она является векторной величиной и описывает силу поля в конкретной точке пространства и объясняет влияние поля на контур (катушку) или элементарные заряженные частицы.

Используя закон правого винта, находится ориентация трасс поля В.

• В физике величина модуля вектора магнитной индукции В прямо пропорционально зависит от максимальной силы, действующей на участок провода, и обратно пропорционально зависит от силы тока в проводнике и длины участка провода:
• B=Fmax/Il.
• Исходя из формулы индукции, ее величина измеряется в особых мерах:
• В=Н/Ам=Тл (Тесла).
• Величина магнитной индукции в один Тесла представляет собой максимальную силу в один Ньютон, которая действует на некий отрезок шунта длиной один Метр, с протекающим в нем током силой один Ампер.
• В зависимости от используемой модели, применяются разные методы вычисления модуля вектора магнитной индукции:

1. Магнитное поле бесконечного прямого провода определяется как:

B=µ0I/2πr, где:

• µ0 – магнитная постоянная, численно равная µ0=4π10-7 Тл×м/А;
• I – ток проводника;
• r – расстояние от измеряемой точки до проводника.

Магнитное поле бесконечного проводника

1. Магнитное поле соленоида:

B= µ0IN/l, где:

• N – число витков соленоида;
• l – длина соленоида.

Соленоидом является катушка с равномерно распределенными витками, длина которой намного больше радиуса.

1. Магнитное поле в центре кругового тока формулируется как:

B= µ0I/2r.

Магнитное поле кругового тока в контуре

Исходя из формул, независимо от выбора источника, генерирующего магнитное поле, модуль вектора магнитной индукции пропорционален силе тока в проводе B~I.

Ток, протекающий в контуре, создает магнитное поле, которое также пронизывает и сам контур. Если в контуре поместить некоторую площадку, то эту площадку будет пронизывать магнитное поле, созданное круговым током в контуре.

Соответственно, через площадку будет проходить некоторый магнитный поток.

Определение величины магнитного потока сквозь плоскую площадку выглядит как:

Φ=BScosα, где:

• B – вектор магнитной индукции;
• S – площадка (площадь);
• α – угол между направлением нормали к площадке S и направлением вектора магнитной индукции В.

1. Учитывая пропорциональную зависимость вектора магнитной индукции от силы тока в контуре, можно прийти к выводу о такой же зависимости силы тока в контуре и магнитного потока Ф~I.
2. Поскольку отношение Ф/I зависит не только от тока контура, но и от площадки S, то данное отношение является характеристикой самого контура и называется индуктивностью контура:
3. L=Ф/I.
4. Индуктивностью контура (катушки) называется физическая величина, равная отношению магнитного потока, созданного током в этом контуре (катушке), к силе тока.

Единицей измерения индуктивности контура (катушки) является отношение Вб(вебер)/А(ампер), называется Гн (генри). Величиной один Генри является индуктивность такого контура (катушки), в котором курсирует ток с силой один ампер, и создается поток в один вебер.

Индуктивность соленоида

• Ток, протекая по цилиндрической обмотке из провода, возбуждает электромагнитное поле. Вектор индукции поля равен:
• B=µ0IN/l.
• Поток магнитного поля соленоида пронизывает каждый из витков соленоида и, соответственно, равен:
• Ф=Ф1N, где:

• Ф1 – поток магнитного поля, пронизывающий один виток;
• N – количество витков провода.

1. Поскольку поле внутри цилиндрической обмотки из провода однородное, то поток магнитного поля,  проходящий через один виток, равен:
2. Ф1=BS= µ0INS/l,
3. а, соответственно, расчет полного магнитного потока соленоида равняется:
4. Ф= µ0INSN/l=µ0IN2S/l.

Поток магнитного поля соленоида

• Вычислив этот поток соленоида, нетрудно определить индуктивность данной катушки (соленоида):
• L=Ф/I= µ0IN2S/lI.
• Сократив обе силы тока в числителе и знаменателе, получаем окончательное выражение, позволяющее определять индуктивность соленоида, или катушки:

Lсол. = µ0N2S/l.

Соленоид приходится частным случаем катушки индуктивности. При расчете катушек используют такое понятие, как относительная магнитная проницаемость вещества внутри катушки, обозначаемая µ. Соответственно,формула индуктивности выглядит как:

L=µ0µN2S/l.

Из формулы видно, что на характеристику катушки влияют некоторые факторы:

1. Количество витков – с ростом численности витков увеличивается количество магнитных линий, пересекающих контур (катушку);
2. Диаметр катушки – потоки в катушке большего диаметра проявляют меньшее компенсирующее воздействие друг на друга;
3. Линейный размер катушки – катушка с большими линейными размерами препятствует формированию магнитного потока;
4. Свойства сердечника – вещество сердечника с лучшей магнитной проницаемостью лучше удерживает магнитный поток.

Формула индуктивности

Имеется большое множество разновидностей катушек индуктивности, отличающихся конфигурацией и областью применения. Ниже предоставлено ряд формул, показывающих, как найти индуктивность катушки:

1. Измерение индуктивности стандартной катушки производится по формуле:

L=µ0µN2S/l, где:

• L – характеристика катушки (Гн);
• µ0 – магнитная const;
• µ – проницаемость вещества сердечника;
• N – количество оборотов проводника;
• S – площадь диаметрального разреза (м2);
• l – активная часть катушки в метрах.

1. Индуктивность прямого проводника:

L=5.081(ln4l/d-1), где:

• L – характеристика катушки (нГн);
• l – размер проводника;
• d – диаметр провода.

1. Определять индуктивности катушек с воздушным сердечником возможно благодаря формуле:

L=r2N2/9r+10l, где:

• L – характеристика катушки (мкГн);
• r – наружный радиус;
• l – активная часть катушки.

1. Индуктивность многослойной катушки с воздушным сердечником:

L=0,8r2N2/6r+9l+10d, где:

• L – характеристика катушки (мкГн);
• r – усредненный радиус катушки;
• l – активная часть катушки;
• d – глубина катушки.

1. Индуктивность плоской катушки:

L=r2N2/6r+11d, где:

• L – характеристика катушки (мкГн);
• r – усредненный радиус катушки;
• d – глубина катушки.

В радиотехнике часто используется сопряжение нескольких катушек. При последовательном или параллельном соединении катушек индуктивности используются различные формулы, находящие общую индуктивность.

1. Суммарная индуктивность, при последовательном подсоединении, рассчитывается как:
2. Lобщ=L1+L2+…+Ln.
3. При параллельном соединении катушек суммарная индуктивность равна выражению:
4. 1/Lобщ=1/L1+1/L2+…+1/Ln.

Катушка индуктивности

От чего зависит индуктивность

Катушкой индуктивности является компонент, состоящий из проводника, намотанного на сердечник, содержащий железо, либо без сердечника. Прибор мультиметр, или LC-метр, ответит на вопрос, как измерить индуктивность катушки. Этим прибором, в основном, пользуются радиолюбители.

Катушки индуктивности в виде тора и цилиндра

К исключительным классам катушек индуктивности относятся дроссели. Дроссель –это такая катушка, целью которой выступает создание в цепи огромного противодействия для переменного тока с целью подавления высокочастотных токов. Постоянный ток через такой дроссель проходит, не встречая препятствия.

При выборе конкретной катушки индуктивности необходимо обратить внимание на некоторые важные параметры, влияющие на работу компонента:

1. Необходимый показатель индуктивности;
2. Предельный ток, на который рассчитан компонент;
3. Допустимый разброс характеристики катушки;
4. Отклонение параметра при колебании температуры;
5. Устойчивость характеристики катушки;
6. Активное сопротивление провода обмотки катушки;
7. Добротность компонента;
8. Диапазон частот, при которых катушка работает без потерь.

Свое применение катушки индуктивности нашли, как в аналоговой, так и цифровой схемотехнике. Конструкция, собранная на катушках индуктивности и конденсаторах, именуемая колебательным контуром, способна усиливать или вырезать колебания определенной частоты.

Использование дросселей в каскадах блоков питания позволяет устранить остатки помех и шумы. Построение таких компонентов, как трансформатор, полностью обязано физическим особенностям катушки индуктивности.

Также катушки индуктивности подразделяются на компоненты с постоянным показателем индуктивности и катушки с переменным показателем индуктивности. Телефонные аппараты, сглаживающие фильтры, цепи высоких частот имеют в своем составе катушки с постоянным значением индуктивности.

Предоставленный материал в полной мере объясняет физические явления: индукция, магнитный поток и индуктивность. В статье рассмотрены разные виды катушек индуктивности, принципы их построения и особенности применения.

Видео

Плотность энергии магнитного поля

Источник: https://elquanta.ru/teoriya/induktivnost-formula.html