Формулы периметра трапеции и примеры применения

Равнобедренная трапеция, её ещё называют равнобокой, имеет равные боковые стороны. Кроме этого, у нее в арсенале есть еще множество интересных и полезных свойств, которые можно с легкостью применять на практике или при решении математических задач.

Определение, признаки и элементы трапеции

Трапецией в геометрии принято называть любой четырехугольник, у которого есть две параллельные друг другу стороны, при том что продолжения других двух сторон пересекаются.

Определение же равнобедренной трапеции идет от того, что у нее боковые стороны эквиваленты по длине.

Свойства равнобедренной трапеции

Существует всего несколько основных свойств, присущих именно данной фигуре. Сейчас мы рассмотрим каждое из них:

1. Прямая, которая проходит через середину оснований такой трапеции, является ее осью симметрии, а также она перпендикулярна ее основаниям.
2. Углы при основаниях трапеции равны.
3. У равнобедренной трапеции также равны и длины диагоналей. Если диагонали перпендикулярны, тогда высота трапеции будет равна сумме основания, деленной на 2.
4. Диагональ разбивает фигуру на 2 треугольника.
5. Биссектрисы углов, принадлежащих одной и той же боковой стороне, всегда перпендикулярны друг другу.
6. Если мы опустим высоту на большее из оснований трапеции, то получим в итоге 2 отрезка АЕ и ЕВ: 

• Первый отрезок АЕ будет равен сумме оснований, деленной на 2, а второй отрезок ЕВ — разности, разделенной на 2:

Периметр равнобедренной трапеции

Эту величину найти очень просто. Простейшей формулой будет сложение всех ее сторон. Однако иногда составители задач не дают нам информацию обо всех из сторон.

В таком случае нам следует в первую очередь найти все стороны фигуры, а затем уже приступать к их сложению.

Как найти стороны трапеции?

1. Существует множество различных способов решения данной задачи, однако мы предложим только некоторые из них.
2. В первую очередь можно найти стороны с помощью средней линии:

• Есть альтернатива, если вам известны высота и угол при большем основании:

Средняя линия

Средней линией в трапеции называется параллельный основаниям отрезок, который делит боковые стороны фигуры на равные части. 

У нее есть множество интересных свойств и теорем с нетрудным доказательством, таких как, например, решение задач на подобие, однако мы на них останавливаться не будем.

Высота трапеции

Высотой трапеции называется самый короткий по длине отрезок, который продолжается ровно от одного основания до другого. Он выполняет своеобразную вспомогательную роль в задачах вплоть до 10 класса с неизвестными сторонами и в тех задачах, где нужно дополнить фигуру до прямоугольника, например.

Для нахождения длины этого отрезка нам необходимо знать оба основания (a и b), а также боковую сторону c. Также полезно было бы знать угол при большем основании α. Формулы здесь довольно простые и не нуждаются в доказательстве.

Диагональ трапеции

Эта линия просто идет от одного угла трапеции к другому, причем эти углы противоположны. В равнобедренной трапеции довольно приятным фактом является то, что диагонали в ней равны друг другу.

А каким образом можно найти длину диагонали? Есть один очень простой способ. Мы можем сделать это, зная все три величины: боковую сторону и каждое из оснований:

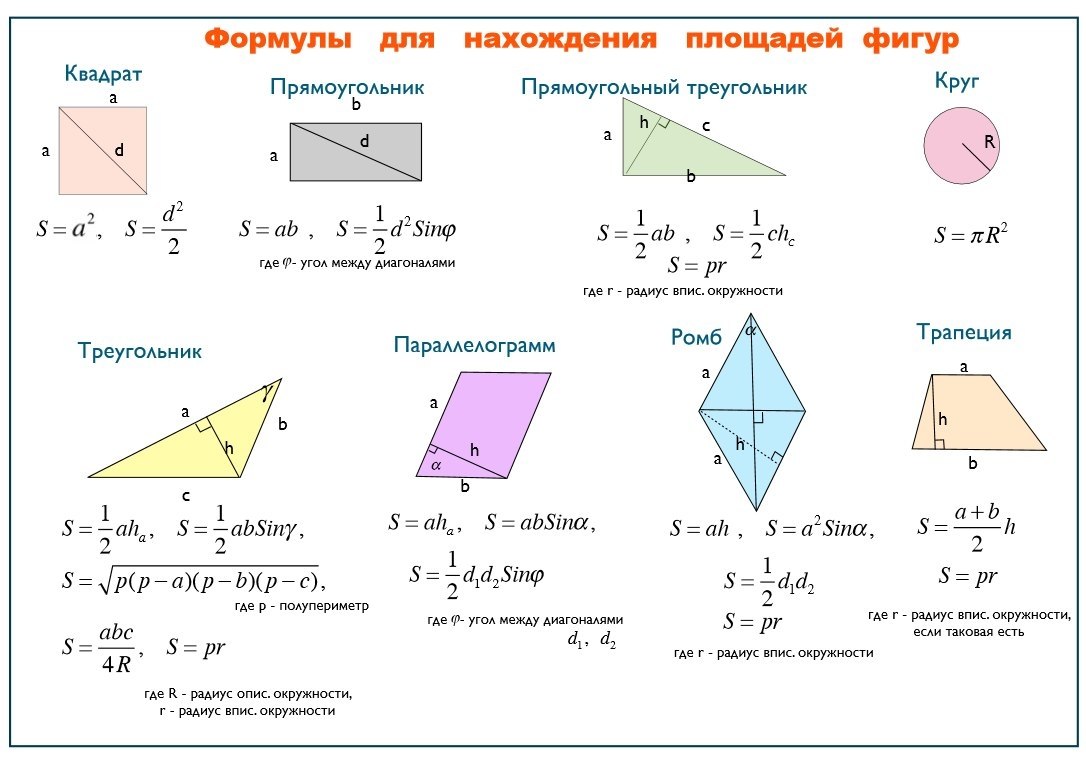
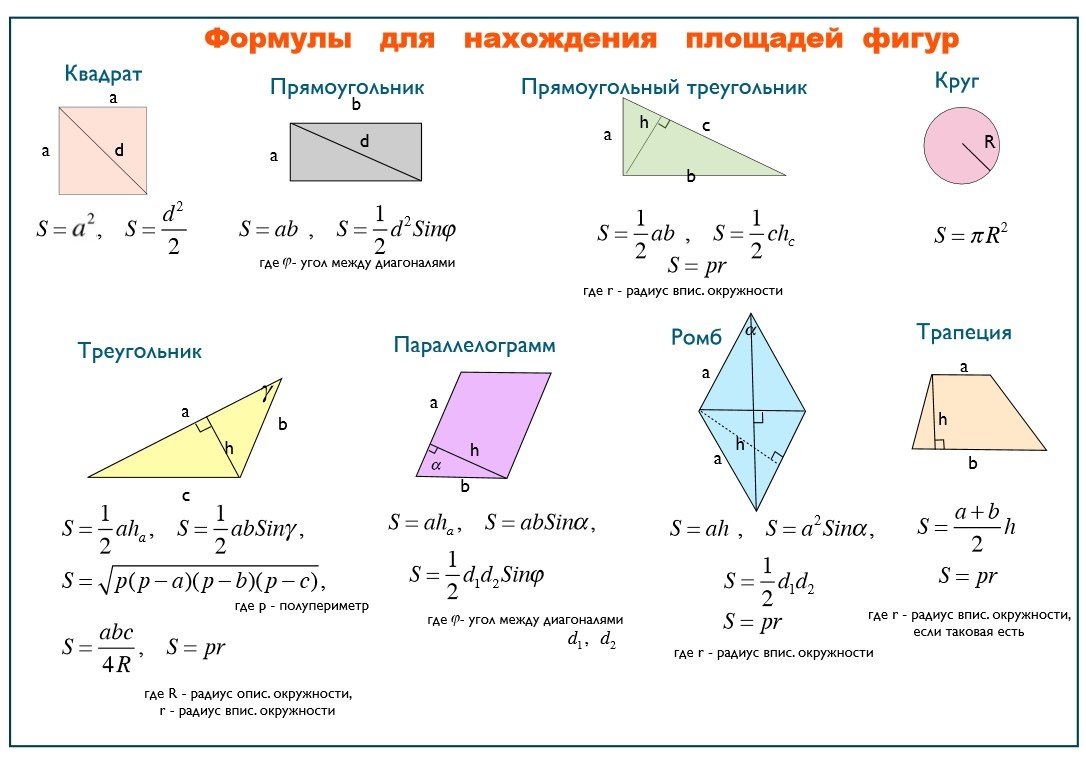
Площадь равнобедренной трапеции

Самой простой формулой является полусумма оснований, умноженная на высоту. Она подходит к любым трапециям.

Для второй формулы нужно знать все стороны трапеции. Это по сути усложненная версия первой, но подойдет она в том случае, если вы не знаете высоту.

 

Это самые базовые формулы, поэтому очень часто используются в различных задачах.

Вписанная и описанные окружности

Интересно, что вписать в трапецию окружность можно только при определенном условии. И это условие выполняется, если мы попарно сложим противоположные стороны нашего четырехугольника, и эти суммы окажутся равны. 

Найти радиус этой окружности не составит труда. Нужно просто разделить высоту пополам.

А вот с описанной окружностью все не так гладко. Есть различные полезные формулы. Например, если диагональ составляет с основанием прямой угол, то диаметр описанной окружности будет равен противоположному основанию трапеции.

Математика бесспорно является матерью всех современных наук. Она по праву занимает свой престол и управляет абсолютно всеми мировыми законами. 

Одной из наиболее интересных подразделений математики принято считать именно геометрию. Ее фигуры также подчиняются математическим правилам и формулам, поэтому она необходима при различных сложных расчетах.

Источник: https://nauka.club/matematika/geometriya/ravnobedrennaya-trapetsiya.html

Свойства трапеции

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Что такое трапеция?

СОДЕРЖАНИЕ СТАТЬИ

Трапеция, вписанная в окружность. ТРАПЕЦИЯ. СРЕДНИЙ УРОВЕНЬ Трапеция. Основные понятия и определения Четвертое свойство трапеции Седьмое свойство трапеции ТРАПЕЦИЯ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.

Вот, смотри:

Оказывается, трапеция (как и треугольник) бывает равнобедренная.

Если боковые стороны равны, то она называется равнобедренной, или равнобокой.

И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ??? И ответ: а вот и нет — тогда это получится НЕ трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма…)

Свойства трапеции… Какие они и что же ты должен знать о них?

Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке   и  )

Почему так? Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что   и   – внутренние односторонние углы при параллельных   и   и секущей  . Поэтому  . И точно так же   и   – внутренние односторонние углы при тех же параллельных   и  , но секущая теперь –  .

Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.

Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:

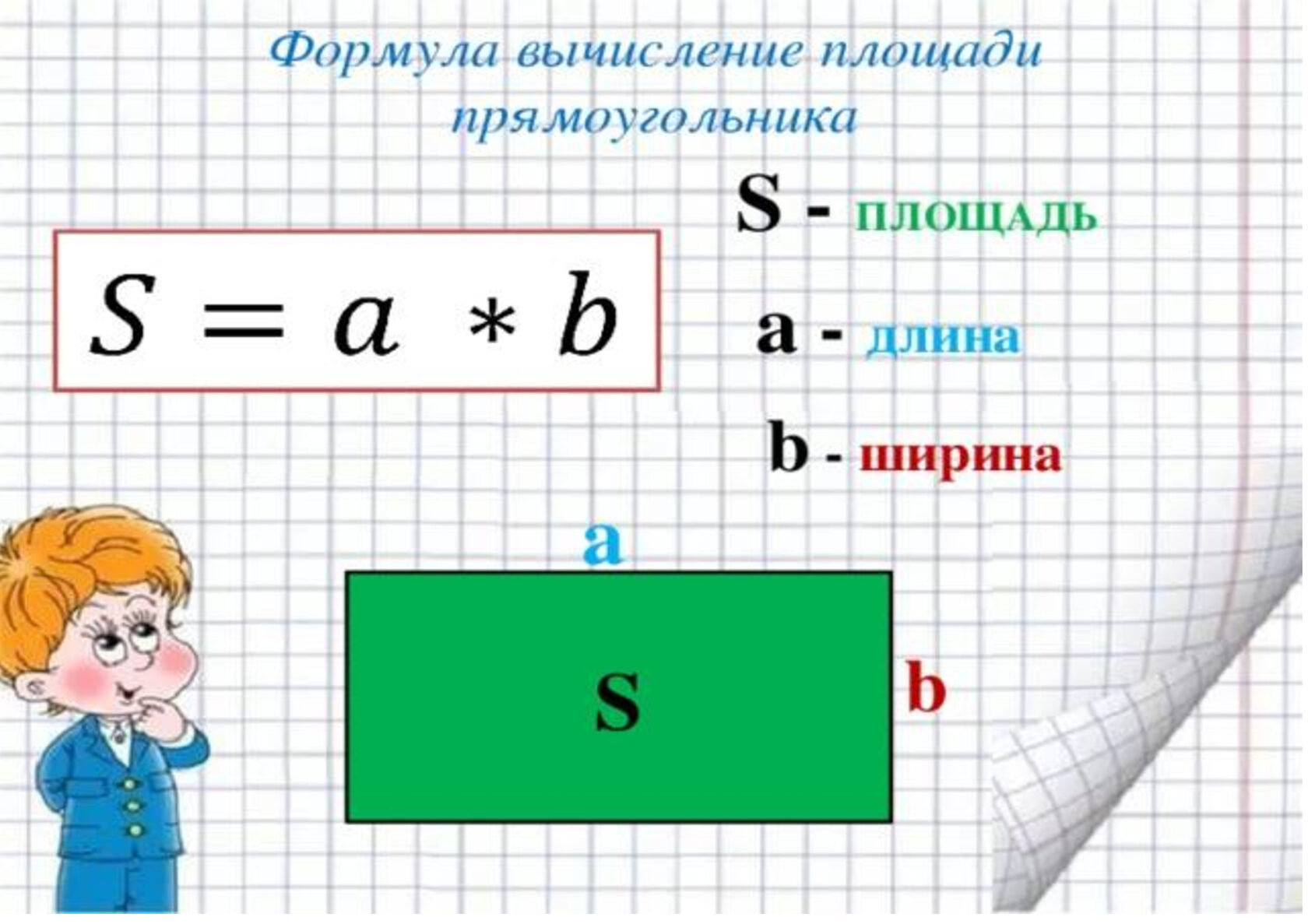Ну вот, а теперь снова порассуждаем об углах.

Опять   и   – параллельные, а диагональ   – секущая. Поэтому  .

А теперь – сразу 2 диагонали и 4 угла:

Что из этого может следовать? Очень важный факт: треугольники   и   – подобны по двум углам. Их коэффициент подобия равен отношению оснований:  .

Средняя линия трапеции

Для начала – что же такое средняя линия трапеции?

Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции.

Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:

, то есть

Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований

А ещё:

Средняя линия трапеции параллельна ее основаниям

Трапеция, вписанная в окружность

Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:

Если трапецию можно вписать в окружность, то она – равнобокая.

Доказывать это мы не будем (здесь во всяком случае), а вот запомнить – хорошо бы – пригодится!

Подведём итог – он короткий. Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.

Так что, если у тебя в задаче трапеция – используй параллельность – всё получится!

ТРАПЕЦИЯ. СРЕДНИЙ УРОВЕНЬ

Трапеция. Основные понятия и определения

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны называются основаниями, а непараллельные – боковыми сторонами.

Если боковые стороны трапеции равны, то она называется равнобедренной или равнобокой.

Свойства трапеции… Какие они и что же ты должен о них знать? Рассмотрим основные свойства трапеции.

Первое свойство трапеции

Сумма угловпри каждой боковой стороне трапеции равна  .

Почему?   и   – параллельны, а   и   – секущие, поэтому:

Второе свойство трапеции

Треугольники   и   подобны по двум углам. (  и   – как накрест лежащие)

Коэффициент подобия треугольников   и   равен отношению оснований:

Третье свойство трапеции

Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

А теперь формула:

А вот и само третье свойство трапеции:

Средняя линия трапеции равна полусумме оснований и параллельна им.

А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!

Итак, проведём  . Тогда четырехугольник   – параллелограмм. Возьмём середину   стороны   и середину   стороны  . Оба:   и   – снова параллелограммы (  и  ;   и  ). Ну вот, значит  , да ещё  .

Поедем дальше.

Проведём   — среднюю линию в  . Знаем, что   и

Что же из всего этого следует?

(так как через точку   можно провести лишь одну прямую параллельную  , поэтому   и   – одна прямая  )

Вот и доказали!

Четвертое свойство трапеции

Если трапеция вписана в окружность, то она равнобокая.

Почему? Подробнее смотри в теме «Вписанный четырехугольник», а тут – двумя строчками:   (трапеция же!)   (вписанный четырехугольник)  . Ну, и так же  .

Пятое свойство трапеции

В ЛЮБОЙ трапеции следующие четыре точки лежат на одной прямой: 1)   – точка пересечения продолжений боковых сторон; 2)   и   – середины оснований; 3)   – точка пересечения диагоналей.

Эту теорему доказывать не будем – не пугайся.

Заметим только, что ВЕРНО и ОБРАТНОЕ:

Если в каком – нибудь четырехугольнике какие – нибудь три из перечисленных четырёх точек окажутся на одной прямой – то четырёхугольник этот – ТРАПЕЦИЯ.

Шестое свойство трапеции

Биссектрисы углов при боковой стороне трапеции перпендикулярны.

Седьмое свойство трапеции

Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд. Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.

В трапеции с перпендикулярными диагоналями

Давай докажем! Это уже целая задача, которая вполне может попасться прямо на экзамене!

Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные. Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.

• Проведём   и  .
• Обозначим  ;  .
• Тогда:

Значит,   (медиана, проведенная к гипотенузе, равна её половине). То есть  . Но ведь   (так как   — параллелограмм)   .

ТРАПЕЦИЯ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).

Сумма углов при каждой боковой стороне трапеции равна 180°:   и

Средняя линия трапеции ( ) – отрезок, соединяющий середины боковых сторон:  .

• Средняя линия параллельна основаниям:  .
• Длина средней линии трапеции равна полусумме длин оснований:  .

Диагонали любой трапеции пересекаются в точке О.

• Треугольники, образованные основаниями трапеции и отрезками диагоналей (  и  ) подобны по двум углам с коэффициентом подобия равным отношению оснований:  .
• Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:  .

Равнобедренная (равнобокая) трапеция — это трапеция, у которой боковые стороны равны:  .

 Свойства равнобедренной трапеции:

• диагонали равны:  ;
• углы при основании равны:  ;
• сумма противолежащих углов равна  :  .

Если трапецию можно вписать в окружность, то она – равнобокая.

Стороны и диагональ равнобокой трапеции связаны соотношением:  .

Площадь трапеции равна полусумме оснований, умноженной на высоту:  .

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!

1. Стать учеником YouClever,
2. Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц», 
3. А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.

можно кликнув по этой ссылке.

 

Источник: https://youclever.org/book/trapetsiya-2

Как найти периметр трапеции?

• Прежде, чем приступить к расчету периметра трапеции, необходимо дать определение понятиям «периметр» и «трапеция», а так же изучить виды трапеций.
• Периметр – это сумма длин всех сторон геометрической фигуры.
• Так же в литературе имеется определение, согласно которому периметр – это длина линии, ограничивающей прямоугольную фигуру.
• Трапеция – четырехугольник, две стороны которого параллельны (основания трапеции), а две другие стороны.

Виды трапеций

• равнобедренная;
• прямоугольная.

1. Если боковые стороны трапеции равны, трапеция называется равнобедренной.
2. 
3. В случае, когда одна из боковых сторон оказывается перпендикулярной основаниям – трапеция прямоугольная.

Определение периметра равнобедренной трапеции

Периметр равнобедренной трапеции определяется по формуле:

Периметр ABCD = a+b+c+d=2*a+b+d , где   a, c – длина боковых сторон; b, d – длина сторон, являющихся основаниями.

Таким образом, если стороны равнобедренной трапеции равны –  а=с=4см, b=5см, d=6см, периметр составит 19 см.: Периметр ABCD = 2*4+5+6=19 см.

Определение периметра прямоугольной трапеции

Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:

Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.

• опустим высоту из вершины С, высота CH = AB = 5см;
• исходя из рисунка 3, AH = BC = 7 см;
• HD = AD – AH = 10 – 7 = 3 см;
• далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
• подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же,  для определения длины различных сторон трапеции могут помочь следующие формулы:

• формула расчета длины основания через среднюю линию;
• формулы длин сторон через высоту и угол при нижнем основании трапеции;
• формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
• формулы длин сторон равнобедренной трапеции через площадь.

Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.

Источник: http://kakumno.ru/najti-perimetr-trapecii.html

Нахождение периметра трапеции: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.

• Формула вычисления периметра
• Примеры задач

Формула вычисления периметра

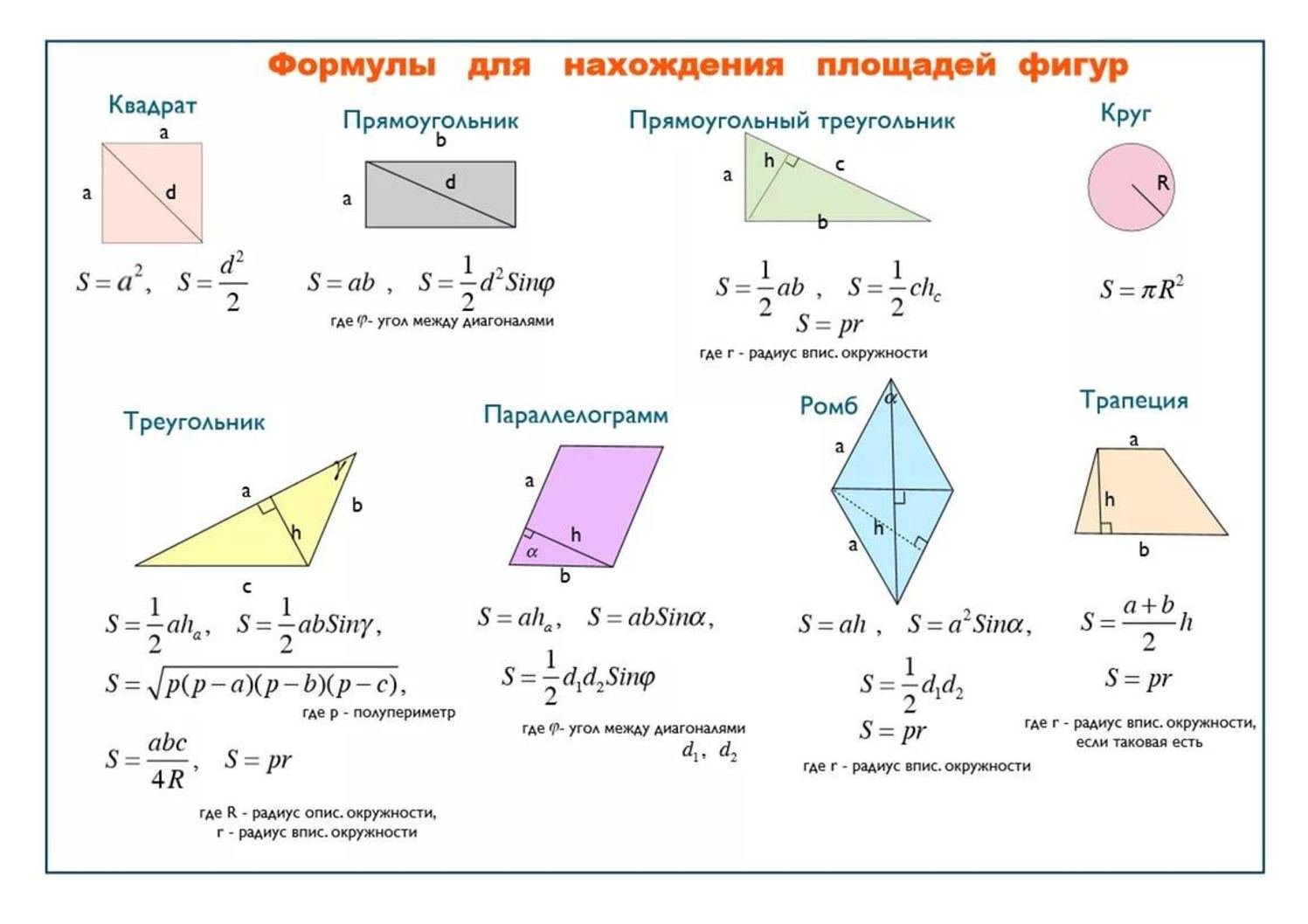
Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

• b и d – основания трапеции;
• a и с – ее боковые стороны.

• Периметр равнобедренной трапеции
• В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:
• P =  2a + b + d или P = 2с + b + d

1. Периметр прямоугольной трапеции
2. Для расчета периметра используется такая же формула, что и для разносторонней трапеции.
3. P = a + b + c + d

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.

Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

Источник: https://MicroExcel.ru/perimetr-trapetsii/

Как найти периметр прямоугольной трапеции

Трапеция – это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.

Шаг 1. Формула вычисления периметра прямоугольной трапеции

Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:

Шаг 2. Решение задач на тему определения периметра прямоугольной трапеции

Задача №1

Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения, и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!

Задача №2

Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD, которая равна a. Одна из боковых сторон CD, которая не перпендикулярна ему, равна d. Угол между этим основанием и стороной равен Альфа.

Решение задачи №2

Катеты находятся по таким формулам: CE = CD*sin(ADC), в свою очередь ED = CD*cos(ADC).

Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа). Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа).

После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.

Задача №3

Требуется найти периметр трапеции, когда даны длины его оснований. AD = a, BC=c. Также мы знаем длину перпендикулярной стороны AB, которая равна b. Острый угол при неперпендикулярной стороне равен Альфа.

Решение задачи №3

Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С.

После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE, а также треугольник ECD (прямоугольный).

Гипотенузой треугольника в нашем случае будет известная нам сторона CD, один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.

Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED.

Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа).

Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.

Оценка статьи:

2

15

Источник: https://imdiv.com/arts/view-Kak-nayti-perimetr-pryamougolnoy-trapecii.html

Как найти периметр трапеции

Трапеция – четырехугольная геометрическая фигура, имеющая две параллельные стороны, которые называются основаниями, и две непараллельные боковые стороны.

Если боковые стороны равны, то фигура называется равнобедренной трапецией. Прямоугольная трапеция – когда одна боковая сторона образует с основанием прямой угол.

Для нахождения периметра трапеции можно воспользоваться одним из методов, в зависимости от исходных данных.

1

Как найти периметр трапеции, когда известна длина боковых сторон и оснований

В этом случае никаких затруднений нет. Воспользовавшись формулой P=a+b+c+d и подставив все известные данные, легко найдем периметр трапеции. Например: a=5, b=4, c=6, d=4. Используя формулу, получаем P=5+4+6+4=19

Данный метод нельзя использовать, если не известна длина хотя бы одной из сторон.

2

Как найти периметр трапеции, когда известна длина боковых сторон, верхнего основания и высоты

Разбиваем трапецию на два треугольника и прямоугольник.

Для того чтобы можно было воспользоваться формулой P=a+b+c+d, необходимо найти нижнее основание. Его можно представить как выражение k+a+n.

Далее воспользуемся теоремой Пифагора. Запишем формулу для первого треугольника c^2=h^2+k^2. После преобразований получаем k=(c^2-h^2)^1/2. Для второго треугольника: b^2=h^2+n^2, итого n=(b^2-h^2)^1/2. После всех вычислений получаем P=a+b+(n+a+k)+c.

Как и в предыдущем методе, необходимо разделить трапецию на прямоугольник и два треугольника. Гипотенузы треугольников являются так же боковыми сторонами трапеции, которые необходимо найти. Меньший катет находим следующим образом.

Воспользовавшись теоремой Пифагора, находим боковые стороны c=(d(1)^2+h^2)^1/2. Далее по формуле P=a+2c+d высчитываем периметр.

4

Как найти периметр трапеции, когда известны нижнее основание, боковые стороны и нижние углы

Рассмотрим пример, когда известны нижнее основание AD, боковые стороны AB и CD, а так же углы BAD и CDA.

Из вершин B и C проводим две высоты, которые образуют прямоугольник и два прямоугольных треугольника. В треугольнике ABK сторона AB является гипотенузой. Осталось найти катеты по формуле BK=AB*sin(BAK) и AK=AB*cos(BAK). Так как BK и CN – высоты, то они равны. По такой же формуле находим ND=CD*cos(CDN). Осталось вычислить BC=AD-AK-ND. Теперь необходимо сложить все стороны и ответ готов.

5

Как найти периметр трапеции, когда известна длина боковых сторон и средней линии

Средняя линия трапеции равна половине суммы длин ее оснований, т.е. f=(a+d)/2. Когда длина оснований неизвестна, но даны размеры боковых сторон и средней линии, периметр находится по формуле P=2*f+c+b.

Как видно, найти периметр трапеции не так уж и сложно. Приступая к решению задачи, нужно лишь определить, какие величины известны и каким методом можно воспользоваться. И тогда решить даже сложную задачу не составит труда.

Источник: https://sovetclub.ru/kak-najti-perimetr-trapecii

Калькулятор периметра трапеции

Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.

Геометрия трапеции

Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет.

Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры.

Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:

• высота — расстояние между параллельными основаниями фигуры;
• средняя линия — отрезок, соединяющий середины боковых сторон.

Данная геометрическая фигура широко распространена в реальной жизни.

Трапеция в реальности

В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:

• дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
• ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
• мода — форма одежды, обуви и аксессуаров;
• архитектура — окна, стены, основания зданий;
• производство — различные изделия и детали.

При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.

Периметр трапеции

• Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
• P = a + b + c + d,
• где a и c – основания фигуры, b и d – ее боковые стороны.

Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.

Примеры из реальной жизни

Платок

Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:

P = 340

Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.

Откосы

К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок.

Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см.

Используем эти данные и получим результат в виде

P = 390

Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.

Заключение

Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.

Источник: https://BBF.ru/calculators/146/

Формула периметра трапеции прямоугольной

Как найти периметр трапеции. Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон.

ru.wikihow.com > Как найти периметр

Периметр трапеции | Формулы и расчеты онлайн — Fxyz.ru

Периметр трапеции, формула. Трапецией называется четырехугольник, две противоположные стороны которого параллельны. Параллелограмм считается частным видом трапеции.

• fxyz.ru > Периметр трапеции |
• Как найти периметр трапеции. Способы вычисления периметра…
• Как найти периметр трапеции. Трапеция – четырехугольная геометрическая фигура, имеющая две параллельные стороны, которые называются основаниями, и две непараллельные боковые…
• sovetclub.ru > Как найти периметр
• Формулы периметра трапеции и примеры применения

ru.solverbook.com > Формулы периметра

1. Периметр трапеции, онлайн расчет
2. Калькулятор периметра трапеции покажет как находить чему равен периметр трапецииТрапеция — это четырехугольник, у которого две стороны параллельны (основание), а две…
3. calc.ru > Периметр трапеции, онлайн
4. Как по формуле найти периметр трапеции ?
5. www-formula.ru > Как по формуле найти
6. Периметр трапеции | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать периметр трапеции онлайн. Для расчета задайте стороны трапеции. Трапеция — четырёхугольник, у которого две стороны…

• mozgan.ru > Периметр трапеции | Мозган
• Периметр трапеции | Онлайн калькуляторы, расчеты и формулы…
• Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции…
• geleot.ru > Периметр трапеции | Онлайн
• Периметр трапеции — онлайн-калькулятор периметра трапеции

Рассчитать периметр трапеции онлайн. Пошаговое решение по основной формуле нахождения периметра трапеции.Периметр трапеции. Содержание. 1. Онлайн-калькулятор.

studwork.org > Периметр трапеции —

Как найти периметр трапеции? Ответ на webmath.ru

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон. В общем случае для произвольной трапеции со сторонами , , , периметр вычисляется по формуле

webmath.ru > Как найти периметр

Онлайн калькулятор который поможет найти периметр трапеции

Используя этот онлайн калькулятор, вы сможете найти периметр трапеции. Воспользовавшись онлайн калькулятором для вычисления периметра трапеции…

ru.onlinemschool.com > Онлайн калькулятор

Как найти периметр трапеции? Ответ на webmath.ru

1. Чтобы найти периметр трапеции необходимо найти сумму длин её сторон. В общем случае для произвольной трапеции со сторонами , , , периметр вычисляется по формуле
2. webmath.ru > Как найти периметр
3. Периметр трапеции | Онлайн калькуляторы, расчеты и формулы…
4. Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции…
5. geleot.ru > Периметр трапеции | Онлайн
6. Периметр трапеции

Вычисление периметра трапеции по длине четырех сторон. Данный калькулятор может быть полезен при проведении проектировочных, бытовых и учебных геометрических расчетах.

ciox.ru > Периметр

Найти периметр трапеции

Данный сервис позволяет найти периметр трапеции. Трапеция – это четырёхугольник, у которого только две из четырёх сторон параллельны. Периметр трапеции равен сумме всех…

algebra24.ru > Найти периметр

Найти периметр трапеции. Как найти периметр трапеции

Что такое периметр? Периметр — это сумма длин всех сторон прямоугольника, к коимПериметр прямоугольной трапеции. Предположим, что нам дана прямоугольная трапеция…

grumy.ru > Найти периметр трапеции.

• Онлайн калькулятор периметра трапеции. Как узнать периметр…
• Для того, что бы вычислить периметр трапеции нам необходимо знать длину ее сторон. Как только нам стала известна длина ее сторон мы можем легко вычислить периметр трапеции по…
• tamali.net > Онлайн калькулятор

Как найти периметр трапеции Как? Так!

Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых…

kak-otvet.imysite.ru > Как найти периметр

Формула периметра трапеции

Периметр равнобокой трапеции. Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.Трапеция будет равнобедренной если выполняется одно из этих условий

calcsbox.com > Формула периметра

Формула нахождения периметра трапеции онлайн

Периметр трапеции. Периметр фигур. Трапецией является плоская геометрическая фигура в виде четырехугольника, у которого имеется две параллельные стороны.

infofaq.ru > Формула нахождения

Как найти периметр трапеции

Как найти периметр трапеции. 3 методика:Основная формулаБоковые стороны не даныВысота или основание не даны. Трапеция – это четырехугольник, у которого две стороны параллельны.

ves-mir.3dn.ru > Как найти периметр

1. Периметр трапеции | Онлайн калькулятор
2. Периметр трапеции – это сумма двух оснований и боковых сторон плоской геометрической фигуры. Онлайн-калькулятор вычисляет периметр как правильной, так и иного вида трапеции…
3. allcalc.ru > Периметр трапеции | Онлайн
4. Как найти периметр прямоугольной трапеции

Шаг 1. Формула вычисления периметра прямоугольной трапеции. Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично.

• imdiv.com > Как найти периметр
• Найдите периметр трапеции
• matematikalegko.ru > Найдите периметр
• Все формулы по теме Периметр трапеции

Периметр трапеции. Трапеция – это четырехугольник, у которого параллельна только одна пара противоположных сторон. a, b – основания трапеции.

formylu.ru > Все формулы по теме

Периметр трапеции. Найти онлайн по формуле

Трапеция — четырехугольник, у которого только две стороны параллельны. Периметр трапеции равен сумме четырех его сторон.

tutata.ru > Периметр трапеции. Найти

1. 100 формул / Периметр трапеции
2. (a, b, c, d) — стороны трапеции.
3. 100formul.ru > 100 формул / Периметр
4. Программа для вычисления периметра трапеции.

Программа предназначена для расчета периметра трапеции.Чтобы найти периметр трапеции, введите значения сторон трапеции, затем нажмите кнопку «ВЫЧИСЛИТЬ».

rapidus.ru > Программа для вычисления

Найти периметр трапеции — Школьные Знания.com

Найти периметр трапеции. Загрузить png. Попроси больше объяснений.Боковые стороны трапеции равны 7 и 12 см. Чему равен периметр трапеции, если в неё можно вписать…

• znanija.com > Найти периметр трапеции —
• Периметр трапеции: онлайн калькулятор, формулы, примеры…
• Трапеция — это особый вид четырехугольника, у которого две противолежащие стороныПериметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин…
• BBF.ru > Периметр трапеции: онлайн

Источник: www.boomle.ru

Источник: https://kak.feedjc.org/formula-perimetra-trapecii-prjamougolnoj/

периметр трапеции формула — Bing

результаты: 269 000Дата Язык Регион

1. • РекламаТрапеция стеклоочист 11170520501502- 2995.00 р. Купить сейчас. Доставка · Москва
2. https://ru.wikihow.com/найти-периметр-трапеции

   Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины …

3. https://ru.onlinemschool.com/math/formula/perimeter

   Формулы периметра. Периметр треугольника, квадрата, прямоугольника, ромба …

4. https://www.fxyz.ru/формулы_по_геометрии/формулы…

   Периметр трапеции, формула. Трапецией называется четырехугольник, две противоположные стороны которого параллельны.

5. https://www.math10.com/ru/geometria/perimetr.html

   Периметр, формулы нахождения периметра. Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра.

6. ru.solverbook.com/spravochnik/formuly-po-geometrii/formuly-perimetra/…

   Все формулы периметра трапеции. В статье описаны формулы вычисления периметра простой и равнобокой трапеции. Теория и примеры решения задач по теме

7. www.treugolniki.ru/kak-najti-perimetr-treugolnika

   Формула периметра треугольника для треугольника АВС . Если назвать треугольник другими буквами, формула периметра треугольника, соответственно, тоже будет выглядеть иначе.

8. https://ru.onlinemschool.com/math/formula/trapezium

   Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция.

9. https://www.webmath.ru/poleznoe/formules10.php

   21.05.2017 · Формулы периметра и онлайн программы для вычисления периметра. См. также: Программа для расчета периметра прямоугольника. Формулы периметра квадрата: 1) Периметр квадрата равен сумме 4-х длин его сторон или …

Источник: https://www.windowssearch-exp.com/search?q=%D0%BF%D0%B5%D1%80%D0%B8%D0%BC%D0%B5%D1%82%D1%80+%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D0%B8+%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0&FORM=R5FD1

Проектная работа Геометрическая фигура трапеция

• Муниципальное автономное общеобразовательное учреждение
• средняя школа №8
• «Геометрическая фигура трапеция»
• Работу выполнили ученицы
• 11 класса МАОУ СШ №8 Соловьёва Арина и Степанова Алина
• Руководитель: Толкачева Наталья Сергеевна, Коптелова Татьяна Анатольевна
• МАОУ СШ №8

с.п. Новосмолинский 2018

Оглавление

Введение………………………………………………………………………2

Происхождение слова «трапеция»………………………………………..3

Трапеция, в повседневной жизни…………………………………………4

Элементы трапеций…………………………………………………………5

Виды трапеций……………………………………………………………….6

Основные свойства трапеции……………………………………………..7-8

Свойства трапеции вписанной в окружность……………………………8

1. Свойства трапеции описанной вокруг окружности……………………9-10
2. Нахождение площади и периметра трапеции.…………………………10-11
3. Решение задач………………………………………………………………12-16

Заключение…………………………………………………………………..17

Литература…………………………………………………………………..18

Введение

В школьном курсе геометрии, в частности по учебнику Геометрия 7-9 авторов Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кодомцева и др.,понятие трапеции вводится как четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Вводятся понятия равнобедренного и прямоугольных трапеций (п.44, §1, Гл.5 учебника). Свойства диагоналей и углов равнобедренной трапеции рассматриваются лишь в задачах №388, 389.

В материалах же различных контрольных работ и экзаменов( ГИА и ЕГЭ) очень часто встречаются задачи на трапецию, решение которых требует знания основных ее свойств ,а также тех, которые в школьном курсе или не рассматриваются совсем, или встречаются лишь при решении задач.

• Цель работы: систематизировать все сведения о трапеции.
• Наши задачи:
• Увидеть применение трапеции в повседневной жизни.
• Повторить весь материал по геометрии за 8-9 класс.
• Показать применение материала при решении задач ГИА и ЕГЭ.
• Выполнить анализ полученных результатов.

Актуальность данной темы определяется необходимостью знать все основные свойства трапеции, уметь решать геометрические задачи при сдаче ГИА, вступительных экзаменов в высшие учебные заведения.

Большинство таких задач не решается с помощью жестких алгоритмов, почти каждая геометрическая задача требует своего подхода.

Здесь уже мало иметь те или иные знания, нужно уметь применять их в каждом конкретном случае.

Проблеманашего проекта заключается в том, что большинство школьников либо не владеют материалом на тему «Трапеция», либо знают его отрывками, либо не могут применить при решении задач на ГИА.

Гипотеза:Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть их на примере задач, то при решении подобных задач на ГИА, вы сможете гарантировать себе дополнительные баллы.

1. Теоретическая часть.
2. Происхождение слова трапеция
3. Трапеция – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две не параллельны

Трапе́ция. Не знаю, как вас, а меня радуют внезапно открываемые этимологией связи между совсем далекими друг от друга словами. Что общего между «трапеция», «трапеза» (еда) и именем турецкого города Трапезунд? А оно есть.

По-гречески «trapedza» значило «стол», «trapezion» — «столик». Из второго слова создалось наше «трапеция» — известная математическая фигура с двумя равными и двумя параллельными сторонами: именно такой формы столы бывали в Греции.

Первое слово — по тем столам, за которыми вкушали пищу монахи византийских монастырей, — начало обозначать и самый этот процесс, еду, — «трапезу»; говорим же мы: «хороший стол», «плохой стол» о еде в каком-нибудь пансионате или доме отдыха. Вы, конечно, сами сообразили, почему «трапецией» называется определенный гимнастический снаряд: конечно, за «трапецеидальную» форму.

А Трапезунд? Над этим приморским городом высится гора, принадлежащая к типу «столовых». Основателями Трапезунда были греки; они и дали ему такое имя: «Город столовой горы».

Происхождение слова трапеция в этимологическом Успенского Л. В.:

Трапе́ция Через нов.-в.-н. Тrареzium — то же из ср.-лат. Trapezium, греч. Τραπέζιον, буквально «столик» (см. Хайзе; Даль 4, 823).

Происхождение слова трапеция в этимологическом Фасмера М.:

ТРАПЕЦИЯ. Заимств. В XVIII в. Из лат. Яз., где trapezium < греч. Trapezion, уменьшит.-ласкат. Суф. Производного от trapeza «стол». Трапеция буквально — «столик». Геометрическая фигура была названа так по внешнему сходству с маленьким столом.

Трапеция, в повседневной жизни

Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.

Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.

Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции – это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.

Элементы трапеции

Элементы трапеции

• Параллельные стороны называются основаниями трапеции.
• Две другие стороны называются боковымисторонами.
• Отрезок, соединяющий середины боковых сторон, называется среднейлинией трапеции.
• Расстояние между основаниями называется высотой трапеции.
• Виды трапеций
• Сейчас нам необходимо разобраться какой бывает трапеция.
• Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой или равнобочной трапецией).

Прямоугольной называют трапецию, один из углов которой является прямым.

И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.

Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

1. Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.
2. Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.
3.  Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.

Основные свойства трапеции

Свойства трапеции… Какие они и что же мы должны знать о них?

Первое свойство:

Сумма углов при каждой боковой стороне трапеции равна 180°.(на рисунке ∠1+∠2=180˚ и ∠3+∠4=180˚)

Почему так? Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что ∠1 и∠2 — внутренние односторонние углы при параллельных AD и BCи секущей AB.Поэтому ∠1+∠2=180˚, ∠1+∠2=180​˚. И точно так же ∠3 и ∠4– внутренние односторонние углы при тех же параллельных AD и BC, но секущая теперь – CD.

• Давай разберем еще некоторые свойства трапеции.
• Второе свойство:
• Ну вот, а теперь снова порассуждаем об углах.
• Опять AD и BC– параллельные, а диагональ AC– секущая.
• Поэтому ∠1=∠2 (накрест лежащие) и треугольники BOC и AOD подобны по двум углам.
• Третье свойство:

Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований, т.е. m=

1. ​​Четвертое свойство:
2. В ЛЮБОЙ трапеции следующие четыре точкилежат на одной прямой:1) E– точка пересечения продолжений боковых сторон;2) F и H– середины оснований;3) G– точка пересечения диагоналей.
3. Свойства трапеции вписанной в окружность

Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.

Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:

• Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.{displaystyle {frac {S_{1}}{S_{2}}}={frac {3,BC+AD}{BC+3,AD}}}
• Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
• 1)2)3)
• Свойства трапеции, описанной вокруг окружности

Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?

1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.

2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.

1. O — точка пересечения
2. биссектрис трапеции ABCD.
3. 3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,
4. и точка O лежит на средней линии трапеции.
5. 4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:
6. AK=AP,
7. BK=BF,
8. CF=CN,
9. DN=DP (как отрезки касательных, проведённых из одной точки).
10. 5.
11. Нахождение площади и периметра трапеции

Площадь трапеции

• Площадь трапеции равна произведению полусуммы ее оснований на высоту:
• S = ((AD + BC) / 2) · BH,
• где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.

Доказательство

Рассмотрим трапецию ABCD с основаниями AD и BC, высотой BH и площадью S.

Докажем, что S = ((AD + BC) / 2) · BH. Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD. Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда

1. SABC = AD · BH / 2, SBCD = BC · DH1.
2. Так как DH1 = BH, то SBCD = BC · BH / 2. Такимобразом,
3. S = AD · BH / 2 + BC · BH = ((AD + BC) / 2) · BH.
4. Теорема доказана.
5. Так же площадь трапеции можно найти с помощью следующих формул:
6. S = mh, где m — средняя линия, h — высота трапеции.
7. Если трапеция равнобедренная, то S = 4r2 / sinα, где r — радиус вписанной окружности, α — угол при основании.
8. , где a, b — основания, c и d — боковые стороны трапеции.
9. Периметр трапеции
10. Итак, подошло время, чтобы узнать формулы нахождения периметра трапеции.
11. Формула периметра произвольной трапеции ABCD (рис. 1), в которой AB=a, BC=b, CD=c, AD=d, имеет вид:
12. В случае, если трапеция ABCD – равнобокая (рис. 2), то есть AB=CD=a, BC=b, AD=c, формула для периметра трапеции примет вид:

Решение задач с применением материала

Пример 1Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?

Решение:

Пример 2. Найдите площадь трапеции с основаниями 18 и 13 и боковыми сторонами 3 и 4.

• Решение.
• Через вершину С меньшего основания ВС трапецииАВСD (ВС =13, AD =18, АВ = 4, CD = 3) проведём прямую, параллель­ную боковой стороне АВ, до пересечения с основанием АD в точке К. Тогда СК=АВ=4,
• DК=АD -АК=АD-BC=18-13=5, CD=3.

ТреугольникKCD прямоугольный, так как KD2=CD2+CK2. Его высота, опущенная на гипотенузу, равна .

Следовательно,SABCD=

Ответ: 37,2

Пример 3.Найдите площадь трапеции, диагонали которой равны 7 и 8, а основания — З и 6.

1. Решение.
2. Через вершину С меньшего основания ВС трапеции АВСD (ВС = 3, AD = 6, BD =8, АС = 7) проведём прямую, параллельную диагонали BD, до
3. пересечения с прямой АD в точке К. Стороны треугольника АСК равны:
4. АC= 7, СК=ВD=8,АК= AD + DК = AD + ВС = 6+ 3= 9. По формуле Герона
5. SACK=
6. а так как треугольники СDК и АВС равновелики, получаем
7. SABCD=SACK=12
8. Ответ: 12

Пример 4. Трапеция ABCD с основаниями АD и ВС (AD > ВС) вписана в окружность с центром О. Известно, что sin LAOB = 5

а средняя линия трапеции равна а. Найдите высоту трапеции.

Решение. Трапеция ABCD вписана в окружность, поэтому она равнобедренная. Обозначим LAOB = α. ПосколькуАОВ — централь­ный угол окружности, а ADB — вписанный,

LADB= = .

ПустьВН — высота трапеции. Тогда DH=т. е. катет DHпрямоугольного треугольника BHD равен средней линии трапеции. Следовательно, ВН = DH tg .

• По условию задачи sin α = , поэтому
• cosα== =
• или
• cosα== = —
• Тогда
• tg
• или
• tg
• Следовательно,BD=αtg .
• Ответ: или.

Пример 5. Найдите площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные —17 и 25.

1. Решение.
2. Через вершину С меньшего основания ВС трапецииАВСD проведём прямую, параллель­ную боковой стороне АВ, до пересечения с основанием АD в точке К.
3. В треугольнике СКD:
4. KD=44-16=28,p=
5. По формуле Герона
6. SCKD== 210
7. C другой стороны, SCKD=
8. Отсюда 210=14h,
9. h=15
10. SABCD=
11. Ответ: 450.

Пример 6. В равнобедренной трапеции основания равны 40 и 24, а её диагонали взаимно перпендикулярны. Найдите площадь трапеции.

• Решение.
• Диагонали АС и ВD пересекаются в точке О.
• Треугольник АОD – равнобедренный и прямоугольный.
• Пусть АО=ОD=x, тогда по теореме Пифагора
• х2+х2=402
• х=20 .
• ОР – медиана треугольника АОD
• По формуле медианы ОР=
• Подставляя в формулу АО=ОD=20 ,AD=40. Получим, ОР=20
• Треугольник ВОС – равнобедренный и прямоугольный.
• Пусть ВО=ОС=у, тогда по теореме Пифагора
• у2+у2=242
• у=12 .
• ОК – медиана треугольника ВОС
• По формуле медианы ОК=

1. Подставляя в формулу ВО=ОС=12 , ВС=24. Получим, ОК=12
2. КР=РО+ОК=20+12=32
3. SABCD=
4. SABCD=
5. Ответ: 1024
6. Заключение

Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») одна из важнейших геометрических фигур, часто используемых в производстве предметов быта, в строительстве, дизайне одежды и т.д.

Поэтому столь скромное место, отведенное в школьном курсе геометрии, можно считать несправедливым. Трапеция, ее свойства заслуживают более подробного изучения не только ради успешной сдачи контрольных работ, экзаменов и т.д.

, но и в знак уважения геометрической фигуры, которая столь часто используется в различных областях своей деятельности современным человеком.

Список литературы:

-Геометрия,7-9: учебн. для общеобразоват. учреждений/ Л.С.Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др. М.: Просвещение, 2008г.

-Геометрия, 10-11 : учеб.для общеобразоват. учреждений: базовый и проф. уровни/[Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].-17-е изд.-М. : Просвещение, 2008.-255 с. : ил.- ISBN 978-5-09-019245-3. –

Трапеция. Свойства трапеции

Источник: https://www.prodlenka.org/metodicheskie-razrabotki/336901-proektnaja-rabota-geometricheskaja-figura-tra