Формула адиабатического расширения

Рассмотрим процесс расширения рабочего тела в адиабатической открытой системе с газодинамическими потерями с привлечением, для наглядности, тепловой диаграммы в T-S-координатах (рис. 1 и 2).

Адиабатичность процесса расширения рабочего тела в открытой термодинамической системе требует только отсутствия теплообмена с внешней средой и постоянства теплоёмкости, но не требует постоянства энтропии, поэтому адиабатичность совмещается с постоянством энтропии в потоке только в изоэнтропном процессе, называемом ещё «идеально-адиабатическим».

Без учёта факторов, связанных с конечной скоростью движения рабочего тела, особенностью теплообмена в движущемся потоке и использованием в анализах и расчётах изоэнтропно заторможенных параметров, термодинамический анализ становится неполным и не отражает общих закономерностей преобразования энергии.

Специфические же вопросы термодинамики — это преобразование располагаемой работы в адиабатном процессе во внутреннюю теплоту в открытых системах, возникающую из-за взаимодействия газодинамических сопротивлений в канале с потоком рабочего тела, не затрагиваются или затрагиваются в минимальном объёме.

В связи с этим раздел термодинамики, посвящённый расширению рабочего тела в открытой адиабатной термодинамической системе, потеряет в значительной степени практический смысл, если не будет учитывать все воздействия, которым подвергается реальный поток.

Обнаружить последствия воздействий на поток газодинамических сопротивлений в открытой системе можно с помощью термодинамического и газодинамического анализов, то есть тепловое сопротивление, которое при обычной трактовке вопроса может рассматриваться как своеобразное явление, не требующее объяснения его физической сущности.

С учётом сказанного, на наш взгляд, для более наглядного представления результатов целесообразно вначале выполнить термодинамический анализ адиабатного процесса расширения рабочего тела в открытой системе с привлечением тепловой диаграммы в координатах T-S. Затем расширить его, с целью более углублённого обоснования преобразований в потоке, за счёт привлечения некоторых теоретических зависимостей.

На рис.

 1 и 2 представлен идеальноадиабатический процесс (то есть процесс без газодинамических потерь), который изображается вертикальными отрезками, расположенными между точками 1* и 1T или изобарами P1* и PT при постоянной энтропии S1 = const. Также показаны адиабатические процессы, которые изображаются пунктирными и прямыми отрезками 1*-2 и 1*-3 при изменяющейся энтропии ΔS ≠ 0, то есть с газодинамическими потерями.

Поскольку изобары в T-S-диаграмме имеют наклон в сторону оси абсцисс, поэтому T3 > T2 > TT, и, таким образом, в процессе течения газа с потерями реализуется разность температур [(T* — T2) или (T* — T3)] меньшая, чем в случае обратимого идеально-адиабатического (изоэнтропного) течения без потерь при максимальном перепаде (T* — TT) (рис. 1 и 2).

Следовательно, действительная скорость рабочего тела Wд на выходе из канала при течении с потерями будет меньше, чем теоретическая WT при течении без потерь. В этом случае абсолютные статические температуры рабочего тела на выходе из канала при течении с потерями будут обозначены как Т2 или Т3.

Увеличение температур Т2 и Т3 относительно теоретической температуры TT, в связи с преобразованием газодинамических потерь в теплоту, влечёт за собой увеличение произведений {Р2V2} или {Р3V3} согласно уравнению Клапейрона и, соответственно, приведёт к увеличению как статических давлений на выходе потока Р2 или Р3, так и удельных объёмов V2 или V3.

Поэтому давления Р2 или Р3 не должны располагаться на изобаре РT = const, как это представлено на диаграмме (рис. 1) [1, 3, 6], а должны перейти на другой уровень статических давлений представленных на диаграмме (рис. 2), где Р3 > Р2 > РT [2].

В связи с этим статическим температурам в движущемся потоке будет соответствовать множество удовлетворяющих состояний при соблюдении основного условия T* = const, то есть Т2 = const, Т3 = const и т. д.

Установить среди них то состояние, которое соответствует искомому решению, можно только с помощью другой координаты.

В предельно-идеальном или теоретически возможном случае другая координата определяется из условия S1 = S2 = S3 = сonst.

Приращение энтропии ΔS в адиабатном потоке является не причиной, а следствием его движения, поэтому определяется только внутренними потерями, зависящими от газодинамических сопротивлений, расположенных в канале. Чем они меньше, тем меньше ΔS и тем меньше действительный процесс расширения отклоняется от изоэнтропного.

Анализируя адиабатный процесс расширения рабочего тела с потерями в открытой термодинамической системе по диаграмме T-S, выделим три характерных перепада температур ΔTT, ΔT2 и ΔTΣ (рис. 1 и 2), где:

• ΔTT = T2 — TT — перепад статических температур в адиабатном потоке относительно изоэнтропного уровня TT;
• ΔT2 = T* — T2 — разница абсолютных заторможенной и статической температуры в адиабатном потоке;
• ΔTΣ = T* — TT = ΔT2 — ΔTT — перепад абсолютных заторможенной и теоретической температуры в изоэнтропном потоке.

В этом случае прежде всего необходимо отметить, что заторможенная температура рабочего тела в адиабатном потоке автоматически поддерживается постоянной, то есть T* = const.

Это значит, что в процессе адиабатного расширения в открытой термодинамической системе присутствует ещё и режим расширения рабочего тела при постоянной заторможенной температуре T* = const, который может быть представлен выражением P1*V1* = P2*V2*, тогда как адиабатный процесс расширения рабочего тела в открытой системе представляется совсем другой зависимостью: P1*V1*m = P2*V2*m, где 1 * и 2 — удельные объёмы на входе и выходе потока; m — показатель адиабатного процесса расширения рабочего тела.

Если решить эти уравнения совместно, то получим те же зависимости, которые уже имеем. Однако в этом случае появляется возможность определить элементарное количество теплоты, но только от одного механического взаимодействия газодинамических сопротивлений с потоком с учётом уравнения состояния при T* = const.

Тогда элементарное количество теплоты, образующееся в процессе расширения реального рабочего тела при постоянной заторможенной температуре в открытой термодинамической системе, будет равно как работе расширения, так и располагаемой работе, и будет выглядеть следующим образом:

где qr.ип — элементарное количество теплоты; lr.расш — работа расширения; lr.расп — располагаемая работа; P1* — абсолютное заторможенное давление во входном сечении; P2* — абсолютное заторможенное давление в выходном сечении; T* — абсолютная температура заторможенного потока; R — удельная газовая постоянная.

• Можно считать, что краткий термодинамический анализ адиабатного процесса расширения рабочего тела в открытой системе с привлечением тепловой диаграммы в координатах T-S выполнен, но его следует расширить с целью более углублённого изучения преобразований в потоке, то есть за счёт привлечения некоторых теоретических зависимостей.
• Теоретические зависимости, учитывающие газодинамические потери, вызывающие внутренний теплообмен при адиабатном расширении газа в потоке, описываются известными дифференциальными уравнениями:
• Δqr = cvΔT + PΔV, (1)
• Δqr = cpΔT — VΔP, (2)
• Δqr = caΔT, (3)
• Δqr = ξWΔW, (4)
• где qr, cp, cv, ca, P, T, V, S, W и ξ — соответственно, удельная теплота газодинамических потерь, удельные теплоёмкости при постоянном давлении, объёме и адиабатного процесса, абсолютные давление и температура, удельный объём, удельная энтропия, скорость газа в потоке и коэффициент газодинамических потерь.
• Совместное решение этих уравнений осуществляется с целью определения показателя адиабатного процесса расширения рабочего тела в потоке m, коэффициента газодинамических потерь ξ, удельной теплоёмкости адиабатного процесса ca и коэффициента внутреннего теплообмена в адиабатном потоке ψ.
• Решая совместно (1) и (3), а также (2) и (3), получим показатель адиабатного процесса расширения рабочего тела в открытой термодинамической системе [2–4]:

где P1* — абсолютное давление заторможенного потока на входе в сечении 1–1; P2 — абсолютное статическое давление в выходном сечении потока 2–2; V1* — удельный объём, определяемый по параметрам заторможенного потока в сечении 1–1; V2 — удельный объём, определяемый по статическим параметрам потока в сечении 2–2; m — показатель адиабатного процесса расширения рабочего тела в потоке. Кроме этого, равнозначный показатель m можно получить и другими путями, которые приведены в литературных источниках [1–5]:

где ξ — коэффициент газодинамических потерь; k — показатель изоэнтропного процесса в открытой системе; — коэффициент скорости; Δqr — элементарное количество теплоты, образовавшейся в потоке за счёт преобразования газодинамических потерь; ΔV — работа расширения рабочего тела.

Обозначим Δqr/(PΔV) = ψ, где ψ — коэффициент внутреннего теплообмена в адиабатном потоке. Тогда выражение (6) будет выглядеть так: m = k — (k — 1)ψ.

Используя выражения (1–6), после несложных преобразований получим:

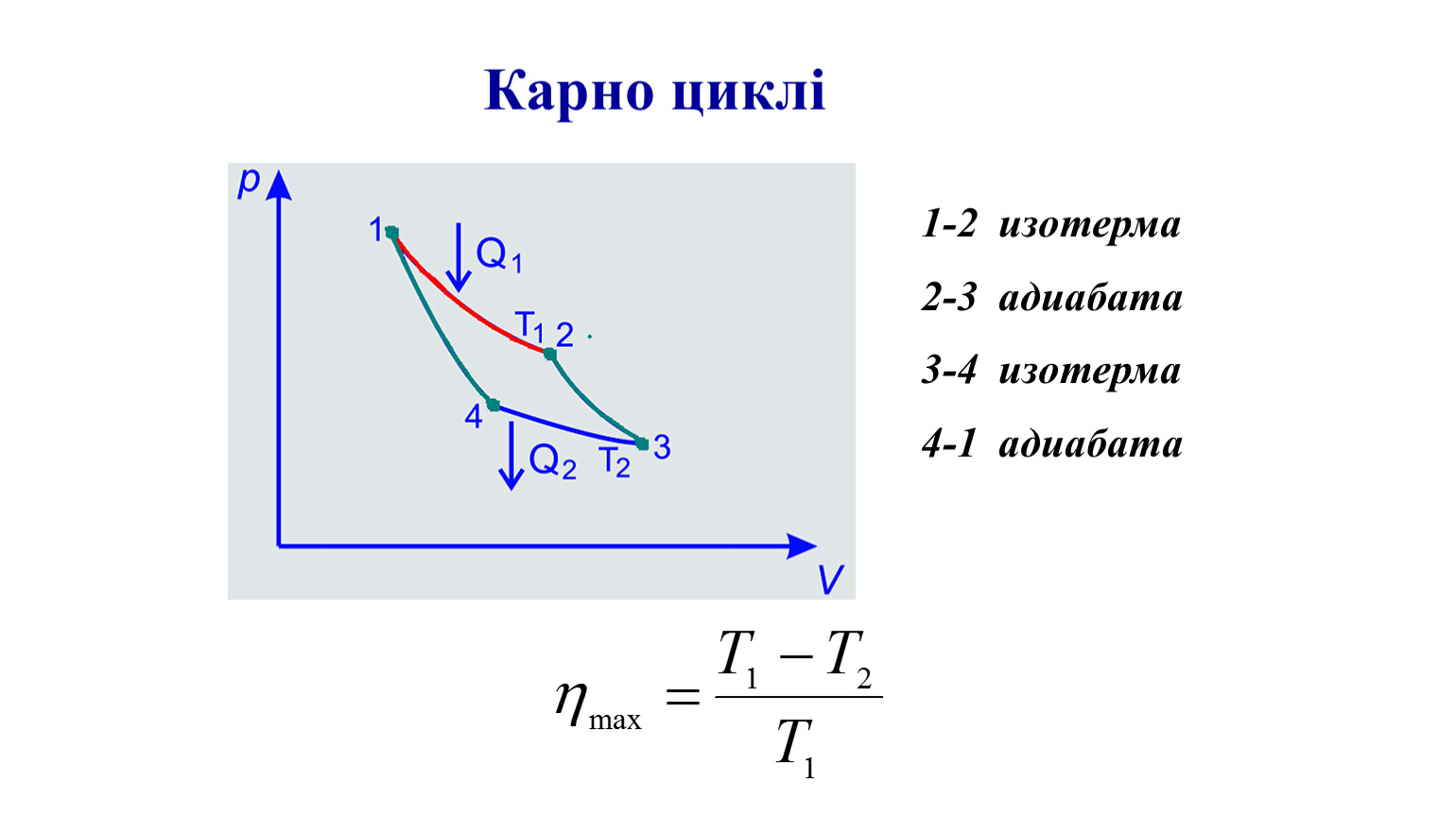
а также:

1. Статическую теоретически достижимую температуру в адиабатном потоке TT определим по выражению, приведённому в [2], с использованием термических параметров потока (рис. 2) ξ = ΔTT/ΔT, откуда после преобразования будем иметь:
2. TT = T2 — ξΔT = (ξ + 1)T2 — ξT*, (9)
3. причём в данной формуле:

• T* — температура заторможенного потока;
• ΔТ = T* — T2 — перепад заторможенной и статической температур в адиабатном потоке.

Кроме того, коэффициент газодинамических потерь ξ можно определить с использованием показателя адиабаты m, приведённом в [2]: Используя зависимость (5) и принимая во внимание, что cp = kcv, получим выражение для определения удельной теплоёмкости ca адиабатного процесса:

Используя зависимость (5) и принимая во внимание, что cp = kcv, получим выражение для определения удельной теплоёмкости ca адиабатного процесса:

• где cp — удельная теплоёмкость при постоянном давлении; cv — удельная теплоёмкость при постоянном объёме.
• Увеличение абсолютной температуры T2 и T3 в адиабатном процессе расширения рабочего тела относительно её изоэнтропного уровня TT вызвано наличием газодинамических потерь, которые, преобразуясь, увеличивают внутреннюю энергию, и определяют её суммарную необратимую часть в адиабатном потоке.
• Анализируя изменения показателей адиабатного m и изоэнтропного k процессов расширения рабочего тела в открытой системе, а также коэффициентов газодинамических потерь ξ, удельной теплоёмкости ca и коэффициента внутреннего теплообмена ψ в адиабатном потоке, как с помощью тепловой диаграммы в координатах T-S, так и приведённых зависимостей, говорит о том, что элементарное количество теплоты, возникающее в потоке как результат преобразования газодинамических потерь, состоит из двух составляющих — механической и термической.
• Вывод

Таким образом, анализ адиабатного процесса расширения рабочего тела в открытой термодинамической системе с помощью тепловой диаграммы в T-S-координатах и приведённых зависимостей говорит о том, что рост изменения энтропии ΔS обеспечивается за счёт роста количества теплоты, образующегося в результате преобразования механической энергии в потоке в теплоту (отрывные течения и др.), которая усваивается текущим рабочим телом. За счёт этого увеличиваются статические параметры в выходном сечении потока и возникает дополнительное термическое сопротивление (рис. 2).

Источник: https://www.c-o-k.ru/articles/analiz-adiabatnogo-processa-rasshireniya-rabochego-tela-v-otkrytoy-termodinamicheskoy-sisteme-s-pomoschyu-teplovoy-diagrammy-v-tskoordinatah

II. Молекулярная физика

Первый закон термодинамики — есть закон сохранения энергии: при любых физических взаимодействиях энергия не возникает и не исчезает, а только передается от одних тел другим или превращается из одной формы в другую.

Общая форма закона сохранения и превращения энергии имеет вид

Согласно первому закону термодинамики, изменение внутренней энергии термодинамической системы при переходе из одного состояние в другое равно сумме работы, выполненной внешними силами, и количества теплоты, переданной системе извне

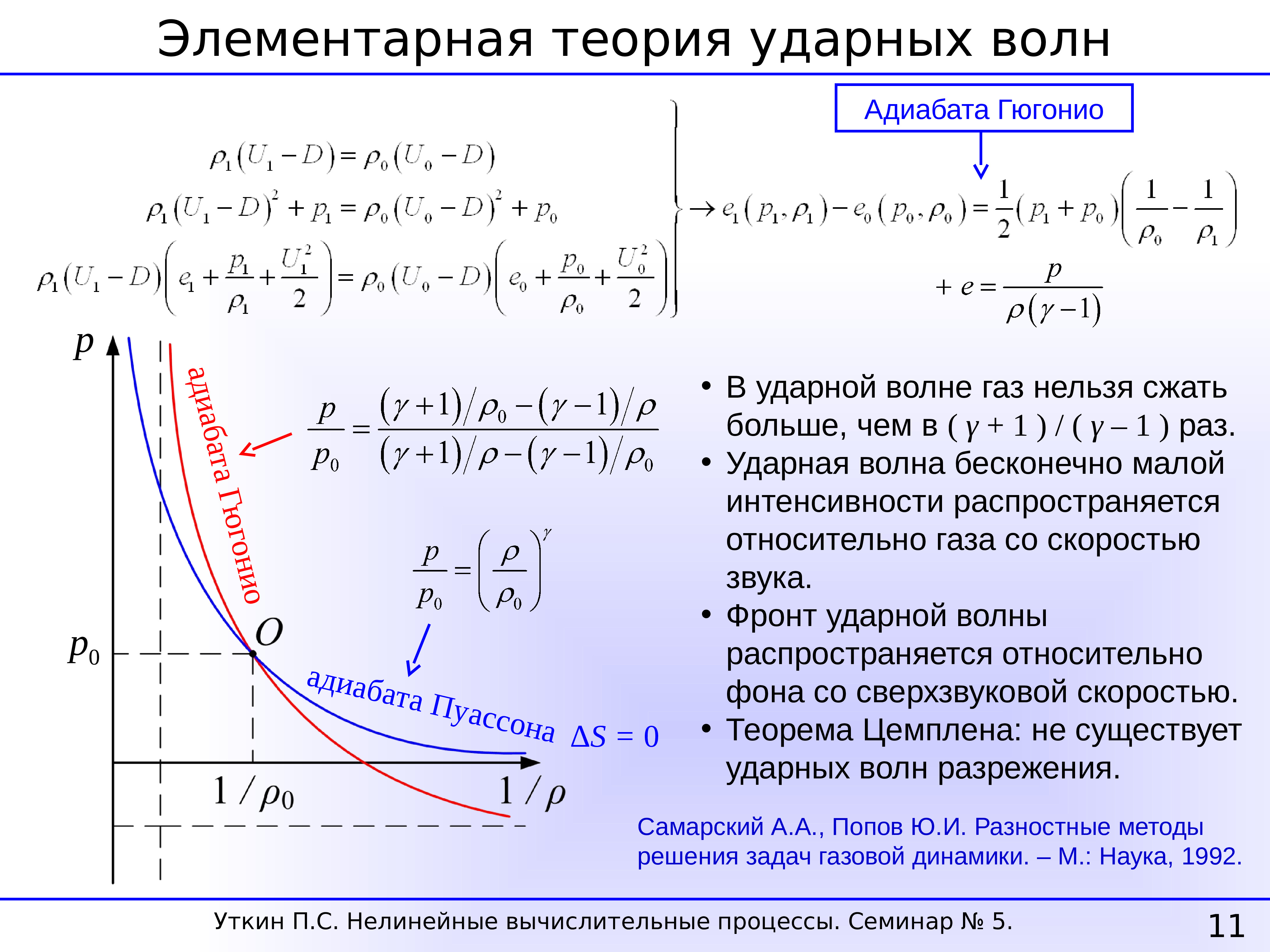
Сформулировать первый закон термодинамики можно иначе: количество теплоты, получаемое системой извне при ее переходе из одного состояния в другое, расходуется на повышение внутренней энергии системы и на работу, которую она выполняет против внешних сил

Например, вы кипятите чайник с водой. Количество тепла расходуется на их нагревание (увеличивается энергия частиц, то есть внутренняя энергия системы), а затем происходит приподнимание крышки — это работа, которую выполняет система.

Внешняя работа над системой равна работе системы, но с противоположным знаком

Адиабатический (адиабатный) процесс

Процесс при тепловой изоляции системы от окружающей среды, то есть

Изменение внутренней энергии происходит только за счет работы внешних сил. Или совершаемая системой работа происходит за счет убыли внутренней энергии.

Практически все реальные процессы происходят с теплообменом: адиабатические процессы — это редкое исключение.

Первый закон термодинамики для изопроцессов

При изотермическом процессе температура не изменяется, значит не изменяется внутренняя энергия

Все количество теплоты, которую получает газ расходуется на выполнение им работы против внешних сил. Или, если газ сжимается, при этом не изменяется температура, работу выполняют внешние силы, а газ отдает некоторое количество теплоты в окружающую среду.

• При изохорном процессе объем не изменяется, значит работа нулевая
• Первый закон термодинамики принимает вид
• В этом случае
• Если газ изохорно охлаждается, его внутренняя энергия уменьшается, и он отдает теплоту в окружающую среду.
• При изобарном процессе первый закон термодинамики имеет общий вид
• Здесь справедливы формулы

Источник: http://fizmat.by/kursy/termodinamika/pervyj_zakon

Адиабатный процесс, его суть и и формулы :

Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Связь с первым началом термодинамики

Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении.

Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю.

Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Следствие из первого начала термодинамики для адиабатического процесса

Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования.

Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения.

Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю.

Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен.

В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона.

Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Примеры адиабатных процессов

Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике.

Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов.

Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.

Источник: https://www.syl.ru/article/206205/mod_adiabatnyiy-protsess-ego-sut-i-i-formulyi

4.9 Адиабатный процесс

Адиабатным называют такой процесс, в котором к системе не подво-дится тепло и от системы не отводится тепло.

При адиабатном процессе должна быть обеспечена идеальная теплоизоляция от внешней среды, в отличие от изотермического процесса, требующего идеального теплового контакта со средой.

В реальных условиях процесс является адиабатным, если система снабжена хорошей теплоизоляцией или если процесс протекает настолько быстро, что не происходит заметного теплообмена с внешней средой.

(4.9.1)

Можно записать и в интегральной форме:

(4.9.2)

Если вещество расширяется и совершает работу над внешними телами, то и, как следует , , т. е. внутренняя энергия вещества уменьшается. Это и понятно: в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – это внутренняя энергия самой системы. Соотношения справедливы для любых адиабатных процессов: равновесных или неравновесных, для любых веществ, находящихся в любых агрегатных состояниях, так как они являются следствием закона сохранения энергии.

Для идеального газа:

(4.9.3)

Отсюда видно, что при адиабатном расширении газ охлаждается , а при адиабатном сжатии газ нагревается , хотя теплота при этом процессе не подводится и не отводится.

Проинтегрировав, найдем работу, совершаемую идеальным газом при адиабатном процессе.

(4.9.4)

Теплоемкость вынесена из-под интеграла, т. к. для идеального газа она не зависит от температуры.

Чтобы найти уравнение адиабаты в переменных подставим вместо p его выражение из уравнения Менделеева –Клапейрона В результате будем иметь

(4.9.5)

Интегрирование последнего соотношения дает

(4.9.6)

Откуда находим

(4.9.7)

Выразим величину через отношение теплоемкостей В результате будем иметь Подставив, получим

(4.9.8)

Последнее соотношение есть уравнение адиабаты (уравнение Пуассона) в переменных T,V. Чтобы записать это уравнение в координатах p,V или T,p нужно произвести замену соответствующих переменных , воспользовавшись уравнением Менделеева – Клапейрона. В результате получим еще два эквивалентных уравнения адиабаты:

(4.9.9)

(4.9.10)

Выражение для работы можно записать иначе. Для этого уравнение адиабаты представим в виде:

(4.9.11)

Отсюда находим

(4.9.12)

Подставляя, и учитывая что
получим

(4.9.13)

Из уравнения Пуассона (4.9.9) следует, что давление идеального газа в адиабатном процессе убывает быстрее, чем в изотермическом процессе , так как всегда и, таким образом, .

Физически это объясняется тем, что при адиабатном расширении давление газа уменьшается не только за счет уменьшения объема, но и по причине происходящего при этом понижении температуры.

Поэтому и работа против меньшего внешнего давления ( для равновесного процесса) при адиабатном процессе будет меньше, чем работа против большего внешнего давления при изотермическом процессе. На рис. 1 работа расширения от объема до объема при адиабатном процессе равна площади фигуры , а при изотермическом – площади фигуры .

рис. 1

Наоборот, при адиабатном сжатии от объема до объема давление газа растет быстрее, чем при изотермическом процессе, так как при адиабатном процессе давление увеличивается не только за счет уменьшения объема, но и вследствие роста температуры газа. Поэтому и работа при адиабатическом сжатии, равная площади фигуры больше работы сжатия при изотермическом процессе, равной площади фигуры .

Источник: http://flash-fizika.narod.ru/4_9.html

Адиабатный (адиабатический) процесс

Согласно первому закону тер­модинамики ΔU = Q + A.

Изотермический, изохорный и изобарный изопроцессы широко применяются в технике.

Так, закон Гей-Люссака положен в основу строения газовых термометров; закон Шарля «ра­ботает» в устройствах, которые называются автоклавами, и т. п.

Термодинамика изучает еще один процесс, широко применяющий­ся на практике, в частности в тепловых двигателях. Это так называемый адиабатный процесс.

Адиабатный процесс — это термодинами­ческий процесс, который происходит в теп­лоизолированной системе, то есть при от­сутствии теплообмена с окружающими тела­ми.

Поскольку в таком случае Q = 0, то в со­ответствии с первым законом термодина­мики вся выполненная работа идет на изме­нение внутренней энергии системы: A = ΔU.

На­пример, создать оболочки с низкой тепло­проводностью (по принципу термоса) или осуществить процесс настолько быстро, что­бы теплообмен между системой и окружа­ющими телами был непродолжительным и им можно было пренебречь.

При адиабатном сжимании га­за вся выполненная работа идет на увеличение внутрен­ней энергии тела: A = ΔU. При адиабатном расширении газа A’ = —ΔU, то есть газ вы­полняет работу за счет умень­шения собственной внутрен­ней энергии.

Рис. 2.5. Графическое изображение адиа­баты

Например, быстрое сжатие газа вызывает возрастание внутренней энергии, которая равняется количеству выполненной работы A, и газ нагревается. На этом явлении, в частности, построено самовозгорание топ­ливной смеси в дизельных двигателях.

И наоборот, если газ сам выполняет работу вследствие стремительного расширения, то его внутренняя энергия уменьшается, и тем­пература газа снижается. Это свойство адиабатного процесса положено в основу сжижения газа.

Примером адиабатного процесса является также взрыв, плавление предохранителя при коротком замыкании и т. п.

Адиабаты, как и изотермы, не перекрещиваются между собой. Материал с сайта http://worldofschool.ru

Графически на координатной плоскости pV адиабатный процесс изображается кри­вой, которая называется адиабатой (рис. 2.5).

Она падает круче, чем изотерма, поскольку при адиабатном процессе изменение дав­ления происходит за счет одновременного увеличения объема и уменьшения темпе­ратуры.

Этот вывод подтверждает также фор­мула (24): p = nkТ, ведь увеличение объема газа ведет к уменьшению концентрации мо­лекул газа, и потому уменьшение давления обусловливают два параметра — температура газа T и концентрация молекул n.

Вследствие адиабатного расширения газа происходит изменение его состояния, которое характеризуется умень­шением внутренней энергии; при адиабатном сжимании газа его внутренняя энергия воз­растает.

На этой странице материал по темам: Вопросы по этому материалу:

Источник: http://WorldOfSchool.ru/fizika/termodinamika/pr-ya-v/processy/adiabatnyj-adiabaticheskij-process

Работа при адиабатическом расширении идеального газа

page id: 114 (Кэшируется)

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором не происходит процесс теплообмена системы с окружающими телами. С точки зрения первого начала термодинамики это означает, что работа совершается газом только за счет внутренней энергии:

Q = ∆U + A = 0;

A = –∆U .

Здесь:

• Q — количество теплоты, полученной газом;
• ∆U — приращение (изменение) внутренней энергии;
• A — работа, совершенная телом при расширении.

Таким образом, работа A, совершенная газом при расширении, равна убыли внутренней энергии –∆U. Положительная работа при адиабатическом процессе практически всегда (за исключением редких случаев) происходит с уменьшением температуры. Для идеального газа внутренняя энергия может быть вычислена по формуле:

U = i/2 νRT,

Здесь:

• i — число степеней свободы 1 молекулы газа;
• ν — количество вещества газа;
• R — универсальная газовая постоянная,
• T — абсолютная температура по шкале Кельвина.

Подставив это выражение в формулу, выражающую первое начало термодинамики для адиабатического процесса, получим:

A = i/2 νR(T1 –T2).

Кривая, соответствующая адиабатическому процессу называется адиабата. Поскольку для идеального газа в таком процессе работа при адиабатическом расширении всегда сопровождается падением температуры, на диагарамме p-V адиабата «спадает» быстрее, чем изотерма. Уравнение адиабаты (уравнение Пуассона) имеет вид:

pV γ = const

Здесь:

• p — давление идеального газа;
• V — объем газа;
• γ = (i + 2)/i — показатель адиабаты,

Адиабатический процесс является частным случаем политропного процесса — термодинамического процесса, проходящего при постоянной теплоемкости. Поскольку в адиабатическом процессе изменение температуры происходит без обмена теплом, теплоемкость при адиабатном процессе равна нулю.

• Изменить масштаб: «CTRL + колесо мыши» или «CTRL + «+»»–«CTRL + «–»»
• Изменить позицию: перетащить при зажатой «CTRL + левая кнопка мыши»
• Стереть все «следы»: «CTRL + F»

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser

(Click here to install Java now)

Модель разработана при помощи системы динамической математики GeoGebra Анухин П.М., преподаватель физики, Аничков лицей Создано: 9.02.2011

Источник: http://school-physics.spb.ru/tiki-index.php?page=virt_thermodynamics_adiabate

Адиабатный процесс в термодинамике

• Связь с первым началом термодинамики
• Влияние первого начала термодинамики на протекающий адиабатический процесс
• Применение адиабатного процесса для расчета тепловых машин
• Термодинамический процесс, происходящий в теплоизолированной системе, либо протекающий с большой (взрывной) скоростью, исключающей передачу тепла в окружающую среду, называется адиабатическим (адиабатным).

Этот процесс характеризуют несколько основных моментов. Например, адиабатический процесс обычно развивается энергично и быстро. В термодинамике все адиабатные процессы протекают, обычно, мгновенно.

В результате обобщения опытных фактов был создан первый закон термодинамики.

Адиабатный процесс производится с большой скоростью, исключающей теплообмен с окружающей средой.

Осуществляется полная теплоизоляция системы от влияния внешней среды.

Связь с первым началом термодинамики

Между первым законом термодинамики и адиабатным процессом прослеживается четкая связь. Первый закон термодинамики гласит – изменение внутренней энергии системы, связанной с развитием термодинамического процесса пропорционально работе, совершаемой данным элементов и изменением количества тепла идеального газа.

Влияние первого начала термодинамики на протекающий адиабатический процесс

Для определения взаимосвязи первого закона термодинамики на адиабатный процесс, нужно представить, что в замкнутой, теплоизолированной системе процесс уже завершился.

Не вдаваясь в незначительные детали и нюансы можно с уверенностью утверждать – газ, расширяясь, совершает работу, при этом уменьшается его внутренняя энергия.

Следовательно, работа, совершаемая при адиабатном расширении газа, производится посредством энергетического потенциала газа.

После открытия и четкого описания адиабатического процесса, физиками произведено большое количество практических экспериментов, приведших к разработке первой теоретической модели, связавшей адиабатный процесс с универсальным циклом Карно.

Эта модель помогла ученым-физикам установить предельные возможности тепловых машин.

У модели есть некоторые недостатки, например с ее помощью сложно описать некоторые природные явления из-за отсутствия изотерм, требующих предварительного определения скорости термодинамических процессов.

Применение адиабатного процесса для расчета тепловых машин

В современной энергетике свыше 90% электрической энергии производится на ТЭС (тепловых электростанциях). Рабочим телом, заставляющим вращаться турбины, является перегретый водяной пар, получаемый при кипении воды.

Отвод тепла в ходе адиабатического процесса при расширении пара, передающего накопленную энергию турбине, осуществляется по изобаре. На реактивных и турбовинтовых двигателях самолетов это явление происходит дважды – при сжатии воздуха и последующем расширении.

Для теоретического обоснования понятия адиабатического процесса, физики-теоретики вывели расчетные формулы.

Для увеличения и стабилизации рабочего потенциала пара осуществляется его перегрев. Перегретый пар под максимально возможным давлением подается на паровую турбину. В результате происходящего адиабатического процесса расширения идеального пара совершается работа, и турбина начинает вращаться.

Ее вращение передается на электрогенератор, вырабатывающий электрическую энергию. КПД системы связан с увеличением давления и температуры перегретого водяного пара.

Из вышесказанного можно сделать вывод, что адиабатный процесс в термодинамике активно используется для производства механической и электрической энергий.

Источник: https://sciterm.ru/spravochnik/adiabatnij-process-v-termodinamike/

ПОИСК

    Изменение энтропии при адиабатическом расширении идеального газа определяют по формуле [c.70]

    Охлаждение газов при их расширении в детандере.

В данном случае расширение предварительно сжатого газа происходит в газовом двигателе, который одновременно совершает внешнюю работу последняя может быть использована для любых целей, например для перекачки жидкостей или нагнетания газов.

Расширение сжатого газа в детандере происходит без обмена теплом с окружающей средой, и совершаемая при этом газом работа производится за счет его внутренней энергии, в результате чего газ охлаждается. Предельная температура охлаждения определяется по общему уравнению (IV, 1) для адиабатического расширения идеального газа. [c.652]

    Вычислите W, AU, АН, AS для процессов перехода идеального газа из состояния 1 (Я,, Тi) в состояние 2 (Р2, Т2) 1) при изотермическом расширении и изобарическом нагревании 2) при изотермическом расширении и изохорическом нагревании 3) при адиабатическом расширении и изобарическом нагревании 4) при адиабатическом расши рении и изохорическом нагревании. [c.92]

    В идеальной форме, как показано на рис. 3.25, простой (т. е.

без промежуточного охлаждения воздуха и регенерации тепла) цикл ГТД (цикл Брайтона) состоит из обратимого адиабатического (изоэнтропийного) сжатия (линия 1—2), подвода тепла при постоянном давлении (линия 2—< ), адиабатического расширения (линия 3—4) и охлаждения при постоянном давлении до начального состояния (линия 4—1). На практике охлаждение достигается непрерывным выпуском отработавших газов и замещением их воздухом из окружающей среды. [c.160]

    Рассмотрим работу идеальной тепловой машины, в которой в качестве рабочего вещества применяется идеальный газ. За счет теплоты, поглощаемой от нагревателя, изменяется состояние газа и совершается работа.

Машина работает по циклу, который состоит из четырех процессов 1) изотермического расширения 2) адиабатического расширения 3) изотермического сжатия 4) адиабатического сжатия. Все процессы проводятся обратимо, и газ после завершения цикла возвращается в исходное состояние. Допустим, что машина работает без трения и не теряет теплоты на лучеиспускание.

Возьмем в качестве рабочего вещества 1 моль идеального газа, начальное состояние которого характеризуется температурой ТI, давлением рх и объемом VI (точка А, рис. 33). [c.95]

    Идеальный газ адиабатически расширяется из объема Vi в вакуум. Вычислить возрастание энтропии, если в конечном состоянии газ имеет объем и показать, что процесс расширения является необратимым. [c.99]

    На таких диаграммах можно легко проследить ход тех изменений, которым подвергается вещество (испарение, конденсация, сжатие, расширение, охлаждение, изменения адиабатические, изотермические, изоэнтальпные и другие).

Для любой точки линии изменения можно быстро найти на диаграмме параметры, характеризующие состояние вещества (энтропию, энтальпию, давление, объем, температуру).

В работе, связанной с развитием технологического метода, когда обязателен, например, выбор оптимального варианта процесса, проходящего при рассмотренных нами изменениях системы, энтропийные диаграммы незаменимы.

    В то время как при адиабатическом расширении любого газа, происходящем с совершением внешней работы, его температура сильно меняется, температура идеального газа при расширении без совершения внешней работы остается постоянной в течение всего процесса. Однако опыт показывает, что при адиабатическом расширении без совершения внешней работы температура реальных газов хотя и незначительна, но снижается снижение его происходит за счет работы внутримолекулярных, так называемых ван-дер-ваальсовых, сил. Это явление носит название холодильного эффекта, для подсчета которого существует ряд эмпирических формул  [c.74]

    Решение. Для определения работы адиабатического расширения воспользуемся уравнением (VI.15). Величину у определим из Ср и Су. Аргон — одноатомный газ. Следовательно, его изохорная теплоемкость на основании молекулярно-кинетической теории идеальных газов равна v= /2 R = 1,5-9,3143 = 12,4715 Дж/(моль К)  [c.47]

    Если разность давлений на длине канала невелика по сравнению с абсолютным давлением в канале, то удельный объем газа с достаточной точностью может быть принят постоянным.

Если же требуется учесть изменение Уг по длине канала, то обычно используют аппроксимацию вида Уг = /(Ян), построенную по данным для состояния насыщения рассматриваемой среды.

При небольших давлениях для описания изменения Юг = 1(Рц) используют, в зависимости от конкретных условий движения среды в канале, адиабатический или изотермический законы расширения идеального газа. [c.82]

    Один пример уже был приведен в 8. В данном параграфе ограничимся рассмотрением квазистатических процессов. Очевидно, вышеупомянутый закон должен быть справедлив для этого специального класса изменений состояний. Примером может служить адиабатическое сжатие или расширение идеального газа, которое осуществляется изменением величин Р я V, связанных уравнением (7.2). [c.46]

    Учитывая условия адиабатического расширения (2.24), состояния равновесия (2.27), полученное выражение (2.26) и уравнение состояния идеального газа, можно показать, что относительная длина витка винтовой линии основной струи равна [c.43]

    При адиабатическом расширении идеального газа его температура понижается (Га < Ti). [c.61]

    Задание. Найдите работу расширения I моль идеального газа при постоянном объеме системы, постоянном давлении, постоянной температуре и в адиабатическом процессе. Используйте общее уравнение (2.1), уравнение состояния идеального газа и первый закон термодинамики. [c.65]

    Почему в формулировках Клаузиуса и Кельвина речь идет о круговом процессе — действуя посредством кругового процесса Потому что, например, при однократном расширении идеального газа по изотерме 1—2 (рис. П1.

3) в принципе возможно поЛное превращение теплоты в работу [вспомните соотношение (П.33), где Qt= Ат. Но нельзя бесконечно расширять газ, и для повторения операции получения второй и т. д. порций работ необходимо будет его сжать. Если сжимать газ при той же температуре Ti, т.

е. по изотерме 2—1 (рис. П1.3), не получится выигрыша работы. Поэтому в цикле Карно газ из состояния 2 расширяют адиабатически до состояния 3, снижая его температуру до T a. Сжатие при T a требует затраты меньшей работы [формула (П.

33)1, а поэтому в целом и получается выигрыш работы, равный площади цикла 1 2 3 4. [c.69]

    Для определения работы при адиабатическом расширении идеального газа используем уравнения (1.8) и (1.12) бЛ — [c.19]

    Отсюда следует, что адиабатическое расширение одного моля идеального газа от до описывается уравнением [c.19]

Примером обратимых процессов может служить адиабатическое расширение или сжатие идеального газа. Однако этот процесс может быть обратим лишь при условии полной тепло-изолированности системы и бесконечно медленного изменения объема и давления газа, необходимого для быстрого выравнивания температуры.

Изотермическое расширение или сжатие идеального газа тоже может быть обратимым процессом при условии немедленного теплообмена с окружающей средой, необходимого для сохранения постоянства температуры. И адиабатический, и изотермический процессы обратимы при условии бесконечно медленного их протекания и исключения трения.

Таким образом, понятие об обратимости процесса вводится в целях установления стандарта для сравнения реальных процессов. [c.46]

    Вычислите максимальную работу а) изотермического и б) адиабатического расширения 2 молей азота от 10 до 20 л (считая его идеальным газом) с начальной температурой 25° С. Примите, что Су — кЯ-Исходя из уравнения J,Jт=(— 1Ср) дН дР)т, выведите формулу [c.23]

    Насколько изменится внутренняя энергия одного моля идеального газа при адиабатическом расширении от состояния с давлением Р и температурой 7 до бесконечно большого объема Какая при этом будет произведена работа  [c.12]

    На этом вывод заканчивается, потому что работа, произведенная на (. идеальным газом при его адиабатическом и обратимом расширении от до У ,. получается путем подстановки последнего выражения в т = Су Т  [c.109]

    Реальные циклы сжижения отличаются от идеального тем, что при дросселировании или адиабатическом расширении сжижается не весь газ, а только некоторая часть его. Несжиженная часть, имеющая низкую температуру, используется для охлаждения вновь введенной порции сжижаемого газа. [c.746]

    Показать, что для обратимого адиабатического расширения идеального газа [c.42]

    Заметим, также, что в отличие от дросселирования адиабатическое расширение сопровождается охлаждением даже идеального газа. Конечная температура газа может быть найдена из соотношения. = (pa/pi) - [c.744]

    Р е ш е н и е. Для определения работы адиабатического расширения поспользуемся уравнением (VI.15). Величину определим из Ср и С /. Аргон — одноатомный газ. Следовательно, его изохорная теплоемкость на основании выводов из молекулярно-кинетической теории идеальных газов = /2 =1,5-8,3143=12,4715 Дж/(моль-К)  [c.49]

    В сосуде при 273 К и 1,01 10 Па находится 10 моль одноатом- юго газа в идеальном состоянии.

Рассчитайте конечную температуру, давление газа и работу процесса расширения газа до объема, в дьз раза превышающего первоначальный а) при медленном изотермическом расширении в цилиндре с поршнем, двигающемся без трения б) п])И адиабатическом расширении в аналогичных условиях в) при мгновенном удалении перегородки между сосудом и вакуумированным просгранством того же объема. Объясните различие результатов, полученных в трех процессах. [c.58]

    Обычно во всех экспериментальных работах давление и температуру определяют непосредственно с помощью манометров и термометров, хотя не менее точные результаты измерений дают и относительные методы. Для определения молярного объема и плотности применяются самые различные методы измерения.

Наиболее простым и прямым путем является определение массы газа и занимаемого им объема, по которым можно найти и = У1п и р = п1У. Непосредственное определение плотности можно также осуществить с помощью метода ядерного магнитного резонанса (ЯМР) и по результатам измерений показателя преломления.

Из этих методов широко известны метод адиабатического расширения (метод Джоуля— Томсона) и метод последовательного изотермического расширения (метод Барнетта). [c.73]

    Но что такое ра.ч(гость те.мператур Эго один из моментов, упу щенных па.

ми пз виду мы также упустили несколько других моментов, Во-первых, мы не определили точно, расширяется или сжимается система мы вычислили изменение внутренней энергии и тем самым — проделанную работу при переходе от некоторого начального состояния в точно не определенное конечное состояние.

Во-вторых, и это важнее, мы даже не определили, производится лп работа в условиях обрати.мостн. И тем не менее уравнение (3,2,23) справедливо для все.х видов адиабатического расширения или сжатия идеального газа, обратимого или необратимого  [c.106]

    Однако практически преимущества детандирования, по сравнению с дросселированием, не столь значительны, как следует нз теоретических соображений.

Действительно, согласно уравнению (IV) для идеального газа, работа адиабатического расширения, при прочих равных условиях, пропорциональна абсолютной температуре газа в первой степени.

Расширение газов в детандере происходит при значительно более низких температурах, чем их сжатие в компрессоре, и поэтому доля расхода энергии, компенсируемая работой детандера, невелика. Она уменьшается еще больше при работе детандера в (збласти, где происходит частичное сжижение газа, т. е.

когда свойства газа весьма значительно отклоняются от законов идеального состояния. Эффективность охлаждения при расширении газа в детандере также заметно снижается вследствие гидравлических ударов и вихреобразования, приводящих к выделению тепла и потерям холода, обусловленных несовершенством тепловой изоляции детандера. [c.653]

    Второй закон термодинамики-тесно связан с обратимостью процессов. Обратимыми называются такие процессы, которые можно реализовать в прямом и обратном направлении так, чтобы система и окружающая ее среда точно вернулись в исходные состояния.

Примером обратимых процессов может служить движение идеальной механической системы, в которой отсутствует трение и другие источники теплоты (математический маятник). Колебания физического маятника не будут обратимыми, так как часть энергии превращается в теплоту трения.

Практически обратимым процессом можно считать адиабатическое или изотермическое расширение или сжатие идеального газа при условии бесконечно медленного протекания процесса и исключенияг всякого трения.

Обратимые процессы являются идеальными предельными случаями реальных процессов. [c.92]

    Для адиабатического процесса йд — О и, следовательно, йи = — РйУ. Таким образом, Сукт = — (1уа и ш =— Су Т2—Т ). Для адиабатического обратимого процесса расширения идеального газа [c.208]

    Затрата работы будет минимальной при идеальном процессе сжижения газа, который можно представить осуществляемым путем изотермического сжатия и адиабатического расширения. Как видно из Т—5-диаграммьг (рис.

517), в таком процессе газ сжимается изотермически при температуре T- от точки А до точки В по прямой ЛВ. После сжатия газ адиабатически расширяется (вертикаль ЙС), превращаясь в жидкость.

Газ подвергается также охлаждению, причем охлаждающей водой от него отнимают не только тепло в количестве, необходимом для сжижения, но и тепло, в[лделивгпееся в результате изотермического сжатия [c.744]

Источник: https://www.chem21.info/info/916632/