Формула работы

Работа — это скалярная величина, которая определяется по формуле

Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.

Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.

Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.

Угол между вектором силы и перемещением

1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.

На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.

Работа силы тяжести

Работа реакции опоры

Работа силы трения

Работа силы натяжения веревки

Работа равнодействующей силы

Работу равнодействующей силы можно найти двумя способами: 1 способ — как сумму работ (с учетом знаков «+» или «-«) всех действующих на тело сил, в нашем примере 2 способ — в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок

Работа силы упругости

Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.

Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу

Мощность

Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле

Коэффициент полезного действия

КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время

Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.

КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.

Главное запомнить

• 1) Формулы и единицы измерения; 2) Работу выполняет сила;
• 3) Уметь определять угол между векторами силы и перемещения

Консервативные (потенциальные) и неконсервативные (непотенциальные) силы*

Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными. Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной.

Формула нахождения работы*

Есть условия, при которых нельзя использовать формулу Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:

1. Значение работы некоторой силы зависит от выбора системы отсчета.

Источник: http://fizmat.by/kursy/zakony_sohranenija/rabota

Механическая работа. Мощность (Зотов А.Е.). Видеоурок. Физика 7 Класс

В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».

Рис 1. Работа в повседневном смысле слова

Мы же будем говорить здесь о работе с точки зрения физики.

Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.

Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.

• Рис 2. Работа – это физическая величина
• Формула  справедлива, когда на тело действует постоянная сила.
• В международной системе единиц СИ работа измеряется в джоулях.

Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.

Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.

Рис 3. Джеймс Прескотт Джоуль (1818 – 1889)

Из формулы для вычисления работы  следует, что возможны три случая, когда работа равна нулю.

Первый случай – когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.

Второй случай – когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.

Третий случай – когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела в направлении действия силы.

Рис 4. Три случая, когда работа равна нулю

Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы. Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).

Предположим, при выполнении строительных работ котлован необходимо засыпать песком. Экскаватору для этого понадобится несколько минут, а рабочему с помощью лопаты пришлось бы трудиться несколько часов. Но и экскаватор, и рабочий при этом выполнили бы одну и ту же работу.

1. Рис 5. Одну и ту же работу можно выполнить за разное время
2. Чтобы охарактеризовать быстроту выполнения работы в физике используется величина, называемая мощностью.
3. Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
4. Мощность обозначается латинской буквой N.
5. Единицей измерения мощности я системе СИ является ватт.

Один ватт – это мощность, при которой работа в один джоуль совершается за одну секунду.

Единица мощности названа в честь английского ученого, изобретателя паровой машины Джеймса Уатта.

Рис 6. Джеймс Уатт (1736 – 1819)

Объединим формулу для вычисления работы  с формулой для вычисления мощности.

• Вспомним теперь, что отношение пути, пройденного телом, S, ко времени движения t представляет собой скорость движения тела v.
• Таким образом, мощность равна произведению численного значения силы на скорость движения тела в направлении действия силы.
• Этой формулой удобно пользоваться при решении задач, в которых сила действует на тело, движущееся с известной скоростью.
• Список литературы

1. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
2. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
3. Перышкин А.В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Physics.ru (Источник).
2. Интернет-портал Festival.1september.ru (Источник).
3. Интернет-портал Fizportal.ru (Источник).
4. Интернет-портал Elkin52.narod.ru (Источник).

Домашнее задание

1. В каких случаях работа равна нулю?
2. Как находится работа на пути, пройденном в направлении действия силы? В противоположном направлении?
3. Какую работу совершает сила трения, действующая на кирпич, при его перемещении на 0,4 м? Сила трения равна 5 Н.

Источник: https://interneturok.ru/lesson/physics/7-klass/rabota-moshnost-energija/mehanicheskaya-rabota-moschnost-zotov-a-e

Определение работы и работа силы трения — успехи современного естествознания (научный журнал)

1
Показано, что общепринятая формула для определения работы справедлива только для частных случаев. Правильное определение работы. Общепринятая формула работы тоже применима только к одному частному случаю.

Вот как определяет сущность работы О.Д. Хвольсон [1, Стр.

91-92] «Сила совершает работу, когда её точка приложения перемещается… …

следует отличать два случая производства работы: в первом сущность работы заключается в преодолевании внешнего сопротивления движению, которое совершается без увеличения скорости движения тела; во втором — работа обнаруживается увеличением скорости движения, к которому внешний мир относится индифферентно. На деле мы обыкновенно имеем соединение обоих случаев: сила  преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела».

Для вычисления работы постоянной силы предлагается формула:

    (1)

где  S — перемещение тела под действием силы F, a — угол между направлениями силы и перемещения. При этом говорят [2], что «если сила перпендикулярна перемещению, то работа силы равна нулю.

Если же, несмотря на действие силы, перемещение точки приложения силы не происходит, то сила никакой работы не совершает.

В [2] также говорится: «Понятие работы как физической величины, введенное в механике, только до известной степени согласуется с представлением о работе в житейском смысле.

Действительно, например, работа грузчика по подъёму тяжести расценивается тем больше, чем больше поднимаемый груз и чем на большую высоту он должен быть поднят.

Однако с той же житейской точки зрения мы склонны называть «физической работой» всякую деятельность человека, при которой он совершает известные физические усилия. Но, согласно даваемому в механике определению, эта деятельность может и не сопровождаться работой.

В известном мифе об Атланте, поддерживающем на своих плечах небесный свод, люди имели в виду усилия, необходимые для поддержания огромной тяжести, и расценивали эти усилия как колоссальную работу. Для механики же здесь нет работы, и мышцы Атланта могли бы быть попросту заменены прочной колонной».

Эти рассуждения напоминают известное высказывание И.В. Сталина: «Есть человек — есть проблема, нет человека — нет проблемы».

В учебнике физики для 10 класса [3, Стр.

138] предлагается следующий выход из данной ситуации: «При неподвижном удержании человеком груза в поле тяжести Земли совершается работа и рука испытывает усталость, хотя видимое перемещение груза равно нулю.

Причиной этого является то, что мышцы человека испытывают постоянные сокращения и растяжения, приводящие к микроскопическим перемещениям груза». Всё хорошо, вот только как рассчитать эти сокращения-растяжения?

Но если шкаф большой массы и большие силы трения, то человек, действуя тем же импульсом силы, шкаф не перемещает, т.е. работа не совершается. Что-то тут не вяжется с так называемыми законами сохранения. Или взять пример, показанный на рис. 1. Если сила F направлена горизонтально ( ), то работа , а если под углом a, то .

Так как , то, естественно, возникает вопрос, куда же исчезла энергия, равная разности работ ( )?

Рисунок 1. Сила F направлена горизонтально ( ), то работа , а если под углом a, то

Приведем пример, показывающий, что работа совершается, если тело остаётся неподвижным. Возьмем электрическую цепь состоящую из источника тока, реостата и амперметра магнитоэлектрической системы. При полностью введенном реостате сила тока бесконечно мала и стрелка амперметра стоит на нуле.

Начинаем постепенно двигать реохорд реостата. Стрелка амперметра начинает отклоняться, закручивая спиральные пружины прибора. Это совершает работу сила Ампера: сила взаимодействия рамки с током с магнитным полем. Если остановить реохорд, то установится постоянная сила тока и стрелка перестает двигаться.

Говорят, что если тело неподвижно, то сила работы не совершает. Но амперметр, удерживая стрелку в том же положении, по прежнему потребляет энергию , где U — напряжение, подведенное к рамке амперметра,  — сила тока в рамке. Т.е.

сила Ампера, удерживая стрелку, по прежнему совершает работу по удержанию пружин в закрученном состоянии.

Покажем, почему возникают подобные парадоксы. Вначале получим общепринятое выражение для работы. Рассмотрим работу разгона по горизонтальной гладкой поверхности первоначально покоящегося тела массы m за счет воздействия на него горизонтальной силой F в течение времени t. Этому случаю соответствует угол  на рис.1. Запишем II закон Ньютона в виде .

Умножим обе части равенства на пройденный путь S: . Поскольку , то получим  или . Отметим, что умножая обе части уравнения на S, мы тем самым отказываем в работе тем силам, которые не производят перемещение тела ().

Кроме того, если сила F действует под углом a к горизонту, мы тем самым отказываем в работе всей силе F, «разрешая» работу только её горизонтальной составляющей: .

Проведем другой вывод формулы для работы. Запишем II закон Ньютона в дифференциальной форме

   (2)

Однако вернемся к нашей задаче о разгоне неподвижного тела. После интегрирования уравнения (2), получим , т.е. импульс силы равен импульсу (количеству движения), полученному телом. Возведем в квадрат и разделив на  обе части равенства, получим

 или    (3)

Таким образом мы получим другое выражение для вычисления работы

где  — это импульс силы. Это выражение не связано с путем S, пройденным телом за время t, поэтому оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным.

В случае, если сила F действует под углом a (рис.1), то её раскладываем на две составляющие: силу тяги  и силу , которую назовем силой левитации, она стремится уменьшить силу тяжести.

Если  будет равна , то тело будет находиться в квазиневесомом состоянии (состояние левитации). Используя теорему Пифагора: , найдем работу силы F

Если сила левитации , то работа левитации будет равна

Это как раз та работа, которую выполнял Атлант, удерживая на своих плечах небесный свод.

А теперь рассмотрим работу сил трения. Если сила трения является единственной силой, действующей по линии движения (например, автомобиль, двигавшийся по горизонтальной дороге со скоростью , выключил двигатель и стал тормозить), то работа силы трения будет равна разности кинетических энергий и может быть рассчитана по общепринятой формуле:

Однако, если тело движется по шероховатой горизонтальной поверхности с некоторой постоянной скоростью , то работу силы трения нельзя вычислять по общепринятой формуле , поскольку в данном случае движения надо рассматривать как движение свободного тела ( ), т.е.

как движение по инерции, и скорость V создает не сила , она была приобретена ранее. Например, тело двигалось по идеально гладкой поверхности с постоянной скоростью, и в тот момент, когда оно въезжает на шероховатую поверхность, включается сила тяги . В данном случае путь S не связан с действием силы .

Если взять путь м, то при скорости  м/с время действия силы будет составлять  с, при м/с время с, при м/с время с. Поскольку сила трения считают не зависящей от скорости, то, очевидно, на одном и том же отрезке пути м сила  совершит гораздо большую работу за 200 с, чем за 10 с, т.к.

в первом случае импульс силы , а в последнем — . Т.е. в данном случае работу силы трения надо рассчитывать по формуле:

        (9)

Зависимость  от , выраженных в долях , показана на рис.2.

• Рисунок 2. Зависимость  от , выраженных в долях
• Рисунок 3. Зависимость суммы ( ) от величины , выраженных так же в долях

На рис.3. показана зависимость суммы ( ) от величины , выраженных так же в долях. Эта сумма имеет минимум, равный  при .

То же самое относится и к случаю равномерного скольжения вниз по шероховатой наклонной плоскости (угол наклона ), когда сила трения равна скатывающей силе  или , т.е. .

В этом случае, чтобы тело равномерно скользило вниз, оно должно получить начальный импульс . Тогда работа силы трения будет определяться не длиной наклонной плоскости S, а временем скольжения :

1.           (10)
2. Учитывая, что , , а , опуская знак «минус», получим
3.          (11)

Зависимость  от K совпадает с графиком (рис.2), только вместо  следует подставить ( ), то же самое относится и к графику на рис. 3.

СПИСОК ЛИТЕРАТУРЫ

1. Хвольсон О.Д. Курс физики. Т. I. Р.С.Ф.С.Р. Госуд.Изд-во, Берлин, 1923.
2. Элементарный учебник физики. Т. I. — М.: Наука, 1972.
3. Касьянов В.А. Физика. 10 класс. Учебн.-М.: Дрофа, 2003.

Библиографическая ссылка

Иванов Е.М. ОПРЕДЕЛЕНИЕ РАБОТЫ И РАБОТА СИЛЫ ТРЕНИЯ // Успехи современного естествознания. – 2005. – № 8. – С. 10-13;
URL: http://natural-sciences.ru/ru/article/view?id=8991 (дата обращения: 01.04.2020).

Источник: https://natural-sciences.ru/ru/article/view?id=8991

Механическая работа — определение, основные формулы и примеры вычислений

Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.

Что такое работа в физике – определение и формула

Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию. 

• В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
• A = F * S
• В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
• A = F * S * cosA

В чем измеряется работа

Физические единицы, в которых выражается механическая работа, – Джоули. 

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах. 

Работа силы трения

При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной. 

Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.

Положительная и отрицательная работа

Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости. 

Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей. 

Полезная или затраченная работа

У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле. 

Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:

КПД = А полезная / А затраченная,

и выражается в процентах. КПД всегда меньше 100.

Мощность

Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:

Р = A / t

В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.

1. Однако при равномерном движении можно использовать и другую формулу:
2. Р = F * v
3. Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.

Примеры решения задач

Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1

Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.

Решение:

Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.

• При помощи простой математики найдем числовой ответ:
• A = 50 м * 10 кг * 10 Н/кг;
• A = 5000 Дж.
• Ответ: 5000 Дж.
• Впрочем, не всегда речь идет о силе тяжести.

Задача 2

Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.

Решение:

Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.

1. Далее при помощи элементарных вычислений рассчитаем ответ:
2. A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
3. Ответ: 0,4 Дж.
4. Но во всех задачах по данной теме траектория движения тела прямая.

Задача 3

Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.

Решение:

В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь.

Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.

• Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
• Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
• В таком случае:
• F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
• Ответ: 5308 Н.
• В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.

Задача 4

Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.

1. Решение:
2. На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы. 
3. Запишем условие в более наглядном виде.
4. Дано:
5. m = 2500 кг;
6. F = 10000 H;
7. t = 10 с;
8. КПД = 30%;

угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);

V – ?

Выведение формулы:

Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).

• A1 = mg;
• A2 = P * t / КПД.
• То есть mg = P * t / КПД.

Шаг 2. P = F * V * cosA.

Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.

1. V = (m * g * КПД) / (F * t * cosA).
2. Числовое решение:
3. V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
4. V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
5. V = 7500 / 50000;
6. V = 0,15 м/с.
7. Ответ: 0,15 м/с.

Источник: https://nauka.club/fizika/mekhanicheskaya-rabota.html

Механическая работа

Механическая работа – это скалярная физическая величина, которая характеризует изменение положения тела под действием силы и равна произведению модуля силы на модуль перемещения (путь).

A = Fs

За единицу измерения работы в СИ принят 1 джоуль.

[А] = 1Н×1м = 1 Дж

• Анализ формулы механической работы:
• 1. Работа силы положительная
  А > 0, если направление силы и направление перемещения совпадают;

Пример: кот падает с крыши. Направление движение кота совпадает с направлением действия силы тяжести. Значит, работа силы тяжести положительная.

1. 
2. 2. Работа силы отрицательна
   А < 0, если направление силы и направление перемещения направлены в противоположные стороны;

Пример: кота подбросили вверх. Направление движение кота противоположно направлению действия силы тяжести. Значит, работа силы тяжести отрицательная.

3. Работа силы равна нулю
А = 0, если
1. под действием силы тело не перемещается, т.е когда s = 0
2. величина силы равна нулю, т.е. F = 0
3. угол между направлениями перемещения и силой равен 90°.

Пример: кот просто идёт по дорожке. Направление движения кота перпендикулярно направлению действия силы тяжести. Значит, работа силы тяжести равна нулю.

• 
• Геометрический смысл механической работы
• Если построить график зависимости значения силы от перемещения (пути), пройдённого телом, то этот график будет представлять собой отрезок прямой, параллельной оси перемещения (пути).
• 

Из рисунка видно, что заштрихованная область под графиком представляет собой прямоугольник со сторонами F и s. Площадь данного прямоугольника равна F • s.
Геометрический смысл механической работы заключается в том, что работа силы численно равна площади фигуры под графиком зависимости силы от перемещения тела.

Источник: https://www.easyphysics.in.ua/category/7class/mechanical_work_and_energy/mechanical_work/

Работа постоянной силы. Мощность. КПД — Техническая механика

§1. Работа постоянной силы

Работа постоянной силы F при прямолинейном движении точки ее приложения равна произведению модуля  силы F на перемещение S и на косинус угла между направлением силы F и перемещения S:       A=F·S·Cos α

Если угол  острый, то работа положительна. В частности, при  элементарная работа A=FS.

Если угол  тупой, то работа отрицательна. В частности, при  элементарная работа A=-FS.

Если угол , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Положительную силу F (α> 90°) называют движущей, а отрицательную (α> 90°) – силой сопротивления.

Единицей измерения работы в системе СИ является джоуль(1 дж= 1 Н∙м). 1 Дж – работа, совершаемая силой 1 Н на 1 м пути.

§2. Консервативные силы

Силы, действующие на тело, могут быть консервативными и неконсервативными.

Сила называется консервативной или потенциальной, если работа, совершаемая этой силой при перемещении материальной точки из одного положения в другое, не зависит от вида траектории (формы пути) и определяется только начальным и конечным положениями тела (рис.1): А1В2 = А1С2 = А12.

Рис.1. Работа консервативной силы 

В случае, если тело движется в обратном направлении А12= –А21, т.е. изменение направления движения по траектории на противоположное вызывает изменение знака работы. Следовательно, при движении материальной точки по замкнутой траектории работа консервативной силы равна нулю (например, поднятие и опускание груза):

Консервативными силами являются силы гравитационного взаимодействия, силы упругости, электростатические силы. Силы, не удовлетворяющие условию (1), называются неконсервативными. К неконсервативным силам относят силы трения и сопротивления. Поле, в котором действуют консервативные силы, называется потенциальным.

§3. Мощность

Мощностьюназывается величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность: P=A/t, гдеt — время, в течение которого произведена работа A. В общем случае мощность рассчитывается: P=FV

Следовательно, мощность равна произведению силы на скорость движения.

Единицей измерения мощности в системе СИ является Ватт(1 вт=1 дж/сек). В технике за единицу мощности часто принимается 1 лошадиная сила, равная  736 Вт.

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы: A=P·t

 Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 кВт-ч = 3,6∙106 Дж).

Из равенства  P=FV  видно, что у двигателя, имеющего дан­ную мощность P сила F тяги  будет тем больше, чем меньше ско­рость движения V. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяю­щие при полной мощности двигаться с меньшей скоростью и раз­вивать большую силу тяги.

§4. Коэффициент полезного действия

            Создавая механизм, важно не только обеспечить движение рабочих органов машины, удовлетворяющих заданному технологическому процессу, но необходимо чтобы машина обладала высоким коэффициентом полезного действия (КПД).

            При наличии сил трения и сопротивления воздуха не вся затраченная работа Аз используется в машинах. Полезная работа Ап всегда меньше затраченной, т.е. Ап

Источник: https://www.sites.google.com/site/tehmehprimizt/lekcii/teoreticeskaa-mehanika/dinamika/rabota-postoannoj-sily-mosnost

Формула работы

ОПРЕДЕЛЕНИЕ

Механическая работа — это произведение силы, приложенной к объекту, смещения, создаваемого этой силой.

A — произведение (может обозначаться как W), F — сила, S — движение.

Единицей измерения работы является Дж (джоуль).

Эта формула применима к телу, движущемуся по прямой и постоянному значению действующей на него силы. Если между вектором силы и прямой, описывающей траекторию тела, существует угол, то формула примет вид:

Кроме того, понятие работы можно определить как изменение энергии тела:

• Именно это применение этой концепции чаще всего встречается в проблемах.
• Примеры решения проблем на тему «Механические работы»
• ПРИМЕР 1

Задача

Перемещение по кругу с радиусом 1 м, тело перемещается в противоположную точку круга под действием силы 9H. Найдите работу, проделанную этой силой.

Решение.

Согласно формуле, работу нужно искать на основе не пройденного расстояния, а перемещения, т. Е. Нет необходимости подсчитывать длину дуги окружности. Достаточно просто учесть, что при движении в противоположную точку круга тело совершает движение, равное диаметру круга, т. Е. 2 м. В соответствии с формулой:

Ответ.

1. Совершенная работа равна A = 18 Дж.
2. ПРИМЕР 2

Задача

Решение

По определению изменение энергии тела — это проделанная на нем работа.

Однако мы не можем найти силу, подставляя исходные данные в формулу, так как мы не знаем движения тела. Мы знаем только его движение вдоль оси OY (обозначим ее через h). Найдите движение тела, используя определение функции sin:

Теперь вы можете заменить все в формуле:

Ответ

Сила равна

Нужны оригинальность, уникальность и персональный подход? Закажи свою оригинальную работу УЗНАТЬ СТОИМОСТЬ

Источник: https://sciterm.ru/spravochnik/formula-raboti/

В чем измеряется работа силы

Слово «работа» имеет несколько значений: результат труда, действие механизма, любая деятельность или её готовый продукт.

В чём измеряется работа, можно говорить лишь после того, как станет понятно, о каком процессе идёт речь.

В физике рассматриваются такие её виды, как: механическая, термодинамическая или работа выхода – количество энергии, приданное отрицательно заряженной частице (электрону) для удаления его из твёрдого вещества.

Работа как составная часть процесса

Определение

Когда на тело действует некоторая сила, заставляющая его проделать путь в определённом направлении, есть смысл говорить о совершённой им полезной работе. Это физическая мера, в механике равна скалярному значению силы, влияющей на тело.

Важно! Работа напрямую зависит от того, куда и в какую сторону действует сила, от её количественного значения, а также от того, как далеко переместится объект, попавший под воздействие этой силы.

Работа силы, приложенной к материальной точке

Сила F→ постоянной величины и направления воздействует на точку. Траектория движения точки прямолинейная. Соответствующая A такой силы будет равна произведению её проекции F→ на направление перемещения (касательную) и длину элементарного смещения точки:

A = Fs*s = F*s*cos(F,s) = F→*s→ ,

где:

• А – работа;
• F→ – сила;
• s→ – вектор смещения.

Как видно из формулы, это произведение скалярное.

Внимание! При таких вычислениях F→ пребывает неизменной в промежутке времени, за которое рассчитывается необходимая работа.

Такая формула справедлива только для прямолинейного перемещения точки и F→ = const.  В противном случае рассчитать работу поможет интеграл:

А = ∫ F→*ds→,

тут интеграл второго рода является криволинейным и суммирует все перемещения по кривой. При этом необходимо принимать перемещения ds→ конечными, в итоге длину каждого сделать стремящейся к нулю.

Приложение силы к реальной точке

Работа сил, приложенных к системе материальных точек

Возникает, когда необходимо измерить значение для сил, влияющих на систему реальных точек. Её можно получить путём сложения работ для сил, способствующих передвижению каждой точки такой системы.

Для случаев, когда тело не представляет собой систему, состоящую из дискретных точек, применяют его мысленное разбиение на элементы. Бесконечно маленький размер такого элемента позволяет считать его материальной точкой. Применение интегрирования вместо дискретной суммы даст возможность рассчитать значение A.

К сведению. Производить математические вычисления допустимо для нахождения работы не только одной определённой силы, но и для любого количества подобных сил, приложенных к точке или системе точек.

Кинетическая энергия

В чем измеряется освещенность

Это часть полной энергии, определяющая энергетику движения. В системе СИ измеряется в джоулях (Дж), в СГС – в эргах (эрг).

• Как связать понятие работы с кинетической энергией? Формула кинетической энергии имеет вид:
• Ek = m*v2/2.
• В этой формуле физическая величина Ek равна 1/2 от массы тела, умноженной на скорость этого тела в квадрате.
• Далее отображается работа сил, воздействующих на точку при помощи 2-го закона Ньютона. Формула закона позволяет через ускорение (а) выразить силу (F):
• F = m*a,
• где:

• m – масса тела;
• a – ускорение тела.

1. Оперируя с кинематическими величинами и обратив внимание на формулу А = F*s, пробуют выразить желаемую взаимосвязь.
2. Случай прямолинейного ускоренного движения, где скорость и перемещение можно выразить формулой:
3. s = v22-v21/2a,
4. где:

• v1 – модуль вектора начальной скорости (в начале участка);
• v2 – модуль вектора конечной скорости (в конце участка).

• Следует подставить значение величины перемещения s и F в формулу работы:
• А = m*a*(v22-v21)/2a = m*v22/2 – m*v21/2.
• Уменьшаемое или вычитаемое, отображаемые во второй части полученного равенства, имеют общий вид:
• m*v/2.
• Это есть кинетическая энергия, её обычно обозначают – Ek.
• Из всего этого следует, что работа, выполняемая над телом, равнодействующих сил, соответствует изменению Ek.

Следует запомнить! Когда сила давит на тело сонаправленно его движению, совершаемая ею работа положительна, и Ek > 0. Когда она приложена навстречу движению тела, тогда  Ek < 0, и работа отрицательная.

Потенциальная энергия

Эта физическая характеристика является частью полной механической энергии. Описывает расположение тела в силовом поле (источнике силы). Причём эта величина может давать оценку только для целой системы. Она бесполезна для характеристики отдельных точек. При этом оценивается не величина, а ее изменение.

Единицей измерения является Дж или Эрг. Наиболее часто применяемые графические обозначения – U, Ep, W.

Различают следующие типы потенциальной энергии:

• в пределах земного притяжения;
• в зоне действия электростатических полей;
• в системах механической природы.

1. Для тела, расположенного поблизости от земной поверхности, формула имеет вид:
2. Ер = m*g*h,
3. где:

• m – масса;
• g – ускорение свободного падения (9,8 м/с2);
• h – высота центра массы тела над нулевым уровнем.

• Уровень нуля можно выбирать произвольно.
• Электрически заряженная материальная точка, имеющая потенциал φ(r→), находясь в зоне электростатического поля, обладает потенциальной энергией Ер. Она вычисляется с помощью выражения:
• Ер = qp* φ(r→),
• где qp – электрический заряд, которым эта точка обладает.

В механических системах при упругих деформациях тела разные его точки взаимодействуют между собой. Такие взаимодействия можно охарактеризовать потенциальной энергией.

1. Упругая деформация может быть записана как:
2. Ep = k*(∆x)2/2.
3. Здесь k – это жёсткость (упругость), ∆x – величина смещения от равновесного положения.

Работа в термодинамике

В чем измеряется работа сил в термодинамике? Термодинамика рассматривает процессы преобразования системы, в результате которых меняется объём. При этом внутреннее изменение энергии тела есть работа.

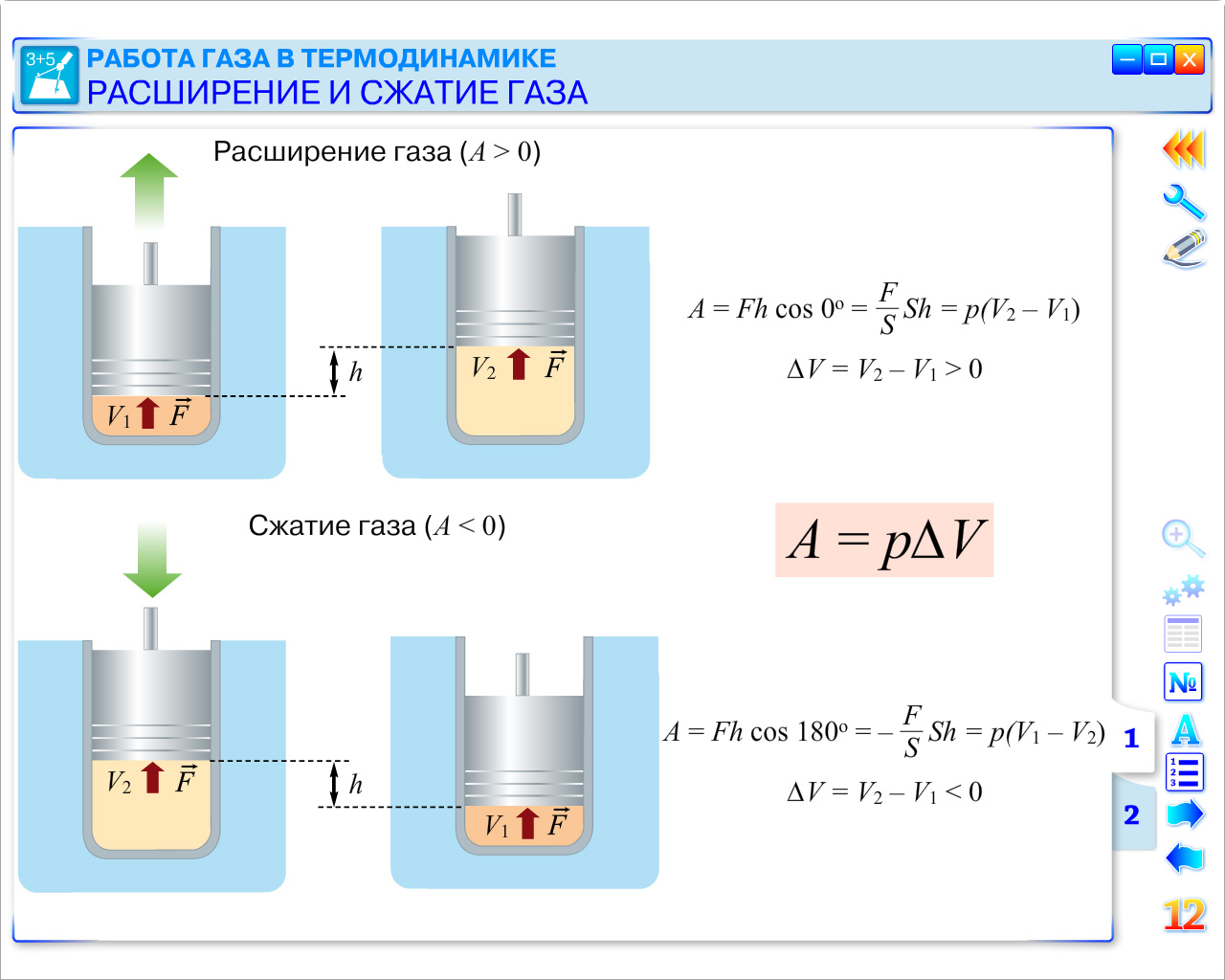
Лучше всего разобрать это на примере  воздействия газа на поршень. Пусть газ давит на поверхность поршня с силой F→’.

Она, согласно 3-му закону Ньютона, направлена в противоположную сторону той силе, с которой поршень воздействует на газ. Это значит, F→’ = – F→.

Единица измерения силы тока

Под давлением газа (p) поршень начинает совершать перемещение ∆h. В случае, если оно мало, то можно говорить о том, что p = const. Тогда работа будет равна A’ = F’*∆h. Можно подставить сюда значение F’= p*S, где S – площадь поверхности, на которую давит газ. После этого выражение примет вид:

A’ = p*S*∆h = p*∆V,

где ∆V – изменение объёма.

Важно! Работа положительная, если газ расширяется. Это обусловлено тем, что поршень движется в ту же сторону, куда направлена F→’. При сжимании газа его работа имеет отрицательное значение, потому как поршень перемещается в противоположную от F→’ сторону.

Работа силы в теоретической механике

• При изучении в теоретической механике преобразований любых форм механического движения в иные типы движения используют понятие работы силы. При расчётах подразумевают, что и направление, и модуль этой силы F постоянны, выражение имеет вид:
• A = F→*s→ = F*s*cos(F→,s→) = F*s*cos α.
• От угла α зависит знак А, от направления зависит величина работы:

• если угол α между направлением силы и перемещением равен нулю, то A = F*s;
• работа А имеет положительное значение, если α меньше 900, и отрицательное, если он больше 900;
• при α = 900 между направлениями силы и перемещения работа равна нулю;
• при α = 0, когда направления F и s совпадают, А = F*s;
• при α = 1800 (сила и перемещение противоположны по направлению), А = – F*s.

Отдельными случаями в теоретической механике рассматривают воздействие сил при перемещениях точек по криволинейным траекториям и их вращениях по оси.

Размерность и единицы

1. Работа, совершаемая в процессах физики, имеет почти одинаковые обозначения, измерять её можно, зная единицы.
2. Основная единица измерения работы – 1 джоуль (Дж). Он равен:
3. 1 Дж = 1 Н*м = 1 кг*м²/с².
4. 1 эрг = 1 г*см²/с² = 1 дин*см = 10−7 Дж.

Работа двигателя внутреннего сгорания соразмерна тяге одной лошади. Одна лошадиная сила равна поднятию лошадью тяжести весом 75 кг. Хотя это не совсем верно.

В данном случае речь идёт о мощности, это не что иное, как работа двигателя, выполняемая им ежесекундно.

• (В*А*с) – это тоже единица измерения, работа, совершаемая электрическим током при перемещении заряженных зарядов по цепи за единицу времени. Сама формула пишется так:
• А = U*I*t,
• где:

• U – напряжение, (вольт);
• I – ток (ампер);
• t – время (cекунда).

Сила трения, которая не только изнашивает трущиеся детали, но и помогает движению транспорта, также совершает определённую работу. Её выполняет и сила тяжести. На определение величины работы тех или иных сил влияют условия, при которых она совершается.

Видео

Источник: https://amperof.ru/teoriya/izmeryaetsya-rabota-sily.html