Формула скорости

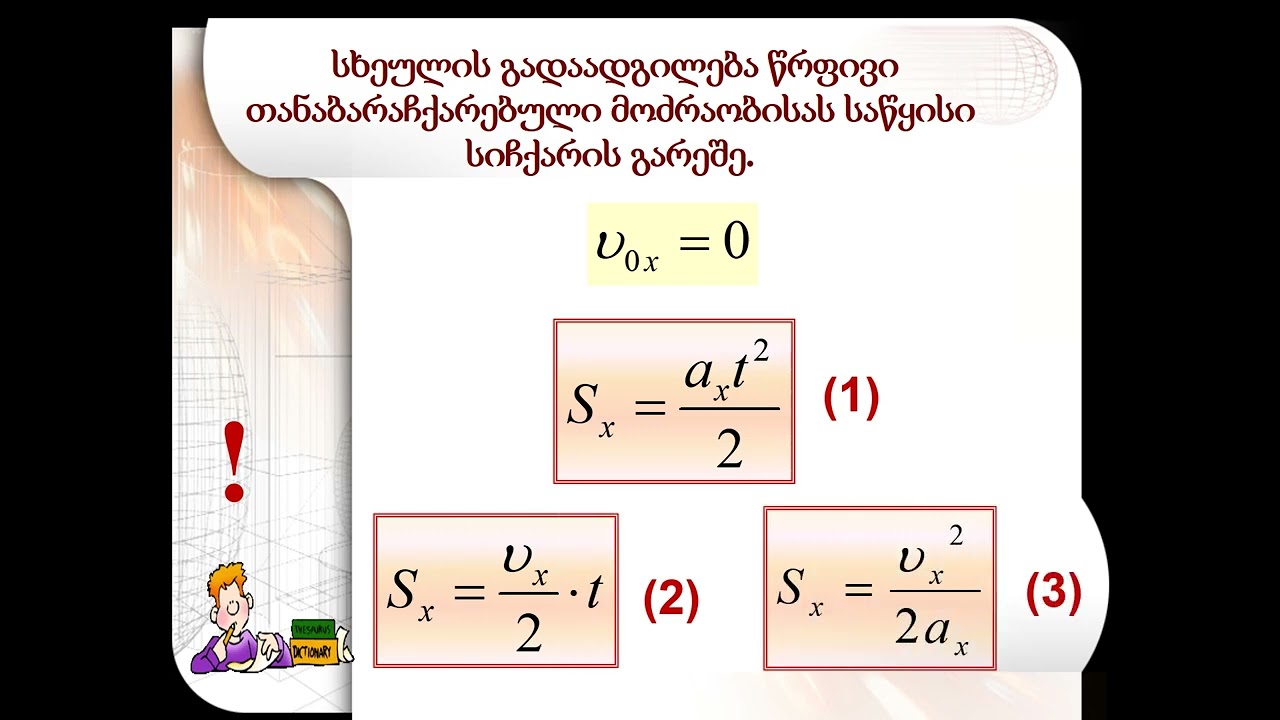
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток.

Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа.

Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник: http://fizmat.by/kursy/kinematika/okruzhnost

Средняя скорость

При решении этих задач обязательно помним, что средняя скорость может быть найдена только делением всего пути на все время движения, даже если какое-то время объект не двигался (делал остановку). Если путь не задан, то необходимо ввести буквенное обозначение длины пути.

Задача 1. Поезд прошел путь 200 км. В течение времени ч он двигался со скоростью км/ч, затем сделал остановку на время мин. Оставшуюся часть пути он шел со скоростью км/ч. Какова средняя скорость движения поезда?

Путь в этой задаче известен. Значит, осталось определить время движения поезда. Кроме того, известно и время его движения на первом участке, значит, нам осталось определить время движения поезда на последнем кусочке, где он двигался со скоростью км/ч. Нетрудно понять, что длина этого отрезка пути равна 100 км, так как поезд уже преодолел 100 км за первый час. Поэтому

•    
•    
• Таким образом,
•    
• Ответ: 50 км/ч

Задача 2. Определить среднюю скорость поезда, если первую половину пути он шел со скоростью км/ч, а вторую половину пути  – со скоростью км/ч.

В этой задаче путь неизвестен. Обозначим его . Тогда время движения поезда на первой половине пути

1. Время движения на второй половине –
2. Средняя скорость – результат деления всего пути, пройденного поездом, на все время:
3.    
4.    
5.    
6.    
7. Ответ: км/ч

Задача 3. Два автомобиля одновременно выехали из Москвы в Петербург.  Один автомобиль первую половину пути ехал со скоростью км/ч, а вторую половину – со скоростью км/ч. Другой автомобиль первую половину времени ехал со скоростью км/ч, а вторую – со скоростью км/ч. Какой автомобиль приедет в Петербург раньше?

Если окажется, что средняя скорость одного из автомобилей больше, чем у другого, то он и должен прибыть раньше. Определим среднюю скорость каждого автомобиля. Первый:

•    
•    
•    
• Второй за первую половину времени прошел:
• За вторую половину времени:
• Тогда его средняя скорость:
• Таким образом, второй автомобиль прибудет раньше.

Задача 4. Найти среднюю скорость самолета, если известно, что первую треть пути он летел со скоростью км/ч, вторую треть – со скоростью км/ч, а последнюю часть пути – со скоростью, вдвое большей средней скорости  на первых двух участках пути.

1. Найдем среднюю скорость самолета на двух первых участках пути.
2. Тогда .
3. Определяем среднюю скорость на всем участке пути:
4. Ответ: 700 км/ч

Задача 5. Найти среднюю скорость поезда, если известно, что на прохождение отдельных участков дистанции, длины которых относятся как , потребовались промежутки времени, находящиеся в отношении , и на последнем участке скорость поезда км/ч. Считать, что на каждом из участков поезд двигался равномерно.

• Определим весь путь по его частям:
• Если , то , , , а весь путь
• Определим время движения поезда на последнем участке, зная его скорость:
• Тогда, так как
• Отсюда найдем :
• Общее время движения:
• Наконец, находим среднюю скорость:
• Ответ: средняя скорость поезда – 40 км/ч.

Источник: https://easy-physic.ru/srednyaya-skorost/

Угловая скорость и угловое ускорение

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

Размерности:

• Количество оборотов за единицу времени [об/мин], [c-1].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П1 в положение П2) – это и есть угловая скорость:

ω=dφ/dt=φ’, рад/с; с-1    (2.3)

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с2], [с-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

• равномерное вращение (ω — const)
• равнопеременное вращение (ε — const)
  ω = ω0+εt;
  φ = φ0+ω0t+εt2/2.    (2.6)

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

ω=n2π/60=nπ/30 рад/с; с-1.

Источник: https://isopromat.ru/teormeh/obzornyj-kurs/uglovaya-skorost-i-uskorenie

Расстояние, скорость, время

В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Расстояние

Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).

Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.

Скорость

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.

100 м : 25 с = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч). 

• У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
• 100м : 25с = 4 (м/с)
• Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
• Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
• 100 м : 50 c = 2 (м/с)
• Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
• Скорость движения первого школьника — 4 (м/с)
  Скорость движения второго школьника — 2 (м/с)
• 4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.

Время

Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.

Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?

1. Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
2. Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
3. 1000 : 500 = 2 (мин)

Время движения обозначается маленькой латинской буквой t.

Взаимосвязь скорости, времени, расстояния

Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

s = v × t

Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.

• Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
• v = 50 (м/мин)
• t = 10 минут
• s = v × t = 50 × 10 = 500 (метров до магазина)

Если известно время и расстояние, то можно найти скорость:

v = s : t

Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?

Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?

1. Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
2. s = 900 метров
3. t = 10 минут
4. v = s : t = 900 : 10 = 90 (м/мин)

Если известна скорость и расстояние, то можно найти время:

t = s : v

Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?

• Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
• Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
• s = 500 метров
• v = 100 (м/мин)
• t = s : v = 500 : 100 = 5 (минут до спортивной секции)

Источник: http://spacemath.xyz/rasstoyanie_scorost_vremya/

Формула зависимости времени, скорости и расстояния: 4 класс. Как найти время, зная скорость и расстояние? Как найти скорость, если известно время и расстояние? Как найти расстояние, если известно время и скорость? График зависимости скорости тела от времени: фото

Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.

Содержание

• Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
• Как найти время, зная скорость и расстояние?
•  Как найти скорость, если известно время и расстояние?
• Как найти расстояние, если известно время и скорость?
• График зависимости скорости тела от времени: фото
• Таблица 4 класс: скорость, время, расстояние
• Примеры решения задач на скорость, время, расстояние за 4 класс
• ВИДЕО: Задачи на движение

Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?

Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса.

Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S. Скорость обозначается буквой  v.

А время, за которое пройден путь, обозначается буквой  t. 

• Путь — S  
• Скорость — v
• Время — t 

Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.

Как зависит время прохождения пути от скорости?

Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.

Как расстояние зависит от времени и скорости?

Как найти время, зная скорость и расстояние?

Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:

Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту . Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?

Как решать задачи для 4 класса?

Как легко решать задачи на движение, где нужно найти расстояние, время или скорость? 

1. Внимательно прочитайте задачу и определите, что известно из условия задачи.
2. Напишите на черновике эти данные.
3. Также напишите, что неизвестно и что нужно найти
4. Воспользуйтесь формулой для задач про расстояние, время и скорость
5. Введите в формулу известные данные и решите задачу

Решение для задачи про Зайца и Волка.

• Из условия задачи определяем, что нам известно скорость и расстояние.
• Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.

В случае опасности заяц может бежать со скоростью 80 км/час

• Пишем в черновик эти данные например так:
• Расстояние до норы — 3 километра
• Скорость Зайца — 1 километр за 1 минуту
• Время — неизвестно
• Теперь запишем то же самое математическими знаками:
• S — 3 километра
• V — 1 км/мин
•  t — ?
• Вспоминаем и записываем в тетрадь формулу для нахождения времени:
•  t = S : v
• Теперь запишем решение задачи цифрами:
•  t = 3 : 1 = 3 минуты

С какой скоростью могут передвигаться разные животные?

Как найти скорость, если известно время и расстояние?

Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:

Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?

Решение задачи на движение:

1. В черновик записываем, что нам известно расстояние и время.
2. Из условия задачи определяем, что нужно найти скорость
3. Вспоминаем формулу для нахождения скорости.

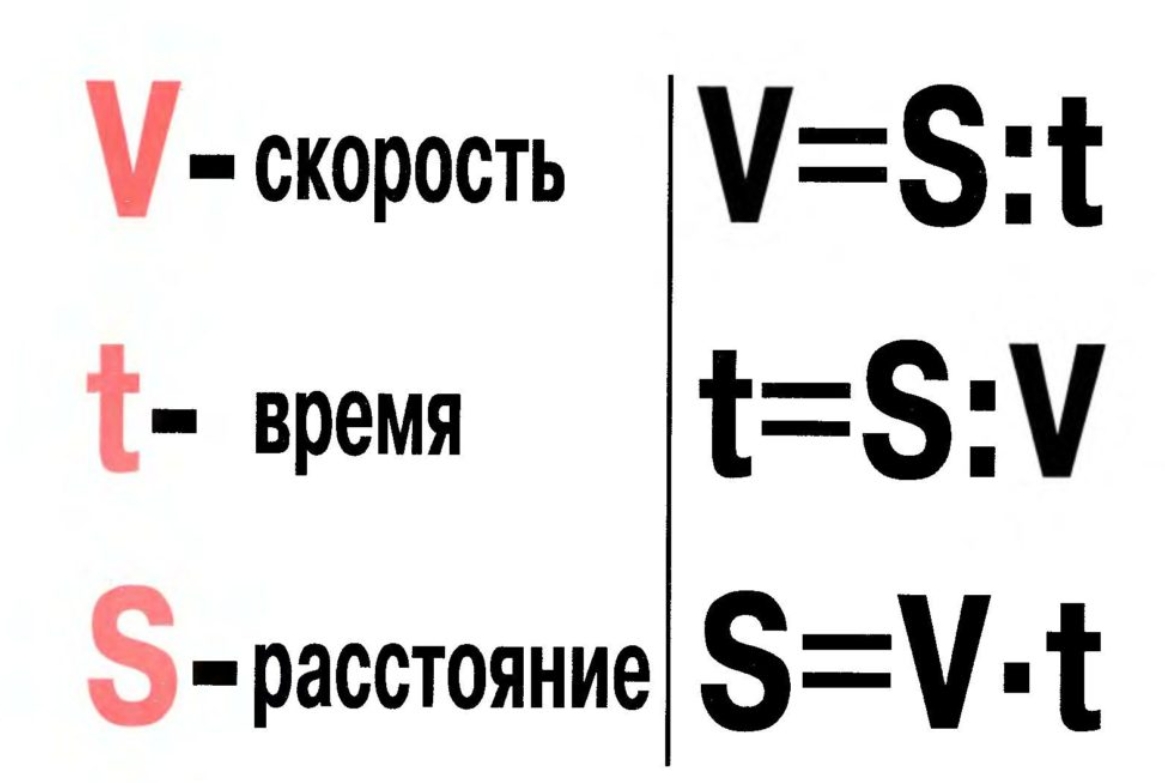
Формулы для решения таких задач показаны на картинке ниже.

Формулы для решения задач про расстояние, время и скорость

1. Подставляем известные данные и решаем задачу:
2. Расстояние до норы — 3 километра
3. Время, за которое Заяц добежал до норы — 3 минуты
4. Скорость — неизвестна
5. Запишем эти известные данные математическими знаками
6. S — 3 километра
7.  t — 3 минуты
8. v — ?
9. Записываем формулу для нахождения скорости
10. v = S : t
11. Теперь запишем решение задачи цифрами:
12. v = 3 : 3 = 1 км/мин

Волк может бежать со скоростью 60 км/час

Как найти расстояние, если известно время и скорость?

Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:

Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?

• Решение задачи: Записываем в черновик, что нам известно из условия задачи:
• Скорость Зайца — 1 километр за 1 минуту
• Время, которое Заяц бежал до норы — 3 минуты
• Расстояние — неизвестно
• Теперь, то же самое запишем математическими знаками:
• v — 1 км/мин
•  t — 3 минуты
• S — ?
• Вспоминаем формулу для нахождения расстояния:
• S = v ⋅ t 
• Теперь запишем решение задачи цифрами:
• S = 3 ⋅ 1 = 3 км

Может быть, они умеют дружить?

Как научиться решать более сложные задачи?

Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

Ребенок, который умеет решать задачи, может гордиться собой

Единицы измерения

Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.

ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.

Единицы измерения для решения задач про скорость, время и расстояние

Для любознательных: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Единицы измерения

Задача про удава: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд.  Какова длина удава? (решение под картинкой)

Как узнать длину удава?

1. Решение: 
2. Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
3. Запишем эти данные:
4. Скорость мартышки — 60 см/сек
5. Скорость слоненка — 20 см/сек
6. Время — 5 секунд
7. Расстояние неизвестно
8. Запишем эти данные математическими знаками:
9. v1 — 60 см/сек
10. v2 — 20 см/сек
11. t — 5 секунд
12. S — ?
13. Запишем формулу для расстояние, если известна скорость и время:
14. S = v ⋅  t 
15. Посчитаем, какое расстояние прошла мартышка:
16. S1 = 60 ⋅ 5 = 300 см
17. Теперь посчитаем, сколько прошел слоненок:
18. S2 = 20 ⋅ 5 = 100 см
19. Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
20. S = S1 + S2 = 300 + 100 = 400 см

График зависимости скорости тела от времени: фото

Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.

Зависимость времени от скорости при движении

Таблица 4 класс: скорость, время, расстояние

В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.

№	Скорость (км/час)	Время (час)	Расстояние (км)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:

1. Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
2. Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
3. Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
4. Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
5. Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?

Задача про самолет

Ответы на приведенные задачи можно найти в таблице ниже:

№	Скорость (км/час)	Время (час)	Расстояние (км)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Примеры решения задач на скорость, время, расстояние за 4 класс

Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:

Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?

• Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
• S = v ⋅  t 
• Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
• S = 10 ⋅ 1 = 10 километров 
• Расстояние, которое прошел Тема считают аналогично:
• S = v ⋅ t 
• Подставляем в формулу цифровые значения его скорости и времени
• S = 5 ⋅ 1 = 5 километров
• Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
• 10 + 5 = 15 километров
• Как научиться решать сложные задачи, для решения которых требуется логически мыслить? 

Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:

Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?

Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.

Кто едет быстрее? Задача про друзей

Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:

Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)

Задача про велосипедистов

Решение:

• 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
• 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
• 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
• 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
• Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
• Ответ: 24 км, 36 км.

Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.

ВИДЕО: Задачи на движение

Источник: https://heaclub.ru/formula-zavisimosti-vremeni-skorosti-i-rasstoyaniya-4-klass-kak-najti-vremya-znaya-skorost-i-rasstoyanie-kak-najti-skorost-esli-izvestno-vremya-i-rasstoyanie-kak-najti-rasstoyanie-esli-izvestn

Как найти скорость, формула

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики.

Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

1

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

2

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

3

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),

S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

V= (S(1)+S(2))/(t(1)+t(2)).

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

• ω = 2π/T, где:
  π – константа ≈3,14,
• T – период.
• Или ω = 2πn, где:
  π – константа ≈3,14,
• n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

1. ω = V/R, где:
   V – численное значение векторной величины (линейной скорости),
2. R – радиус траектории следования тела.

5

Как найти скорость – сближение и отдаление точек

• В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.
• Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
  V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.
• Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

6

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Источник: https://sovetclub.ru/kak-najti-skorost-formula

Формула средней скорости движения

Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории

Средняя скорость движения —  это отношение полного пути пройденного объектом на общее время затраченное на это путешествие

Естественно предположить, что если объект часть общего пути прошел за одно время,  другую часть  за другое время, а третью за третье время, то  средняя скорость  будет являтся отношением  всех частей пути на все затраченное время.

А если  известно  например  части пути и скорость объекта на каждом пути ?  Не среднее арифметическое же брать от всех скоростей… хотя очень часто  именно так и поступают впервые большинство учеников, да и взрослых тоже

На самом деле, при известных частях пути и скоростей на участке формула будет следующая

наверняка догадались как она получилась из предыдущей формулы.

Если в задании пути буду обозначаться как часть от общего ( например,  первая половина пути, 2/3 пути и т.п.) то, учитывая  что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость  будет определятся как

Пример: 

Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.

Решение:

Ответ: 60 км/час

И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.

Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час.

Какое расстояние  между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час

Смотрим вот на эту формулу    и думаем

Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)

Теперь со временем

На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути.  Не пугайтесь что получилось «время  равно одной десятой пути». Оно потом понадобится..

Время на втором участке известно и равно 1 час

Напишем нашу формулу по полученным данным

Выразим расстояние от точки А до точки Б через среднюю скорость и получим

Поставим значение средней скорости  получим что общее расстояние которое преодолел пешеход равно  4 километра и почти 286 метров

Сложновато? Зато интересно и увлекательно.

Из последней формулы  вытекает  «парадоксальный» вывод: При средней скорости приближающейся к 10 км/час  расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще  становится отрицательным.

Что хотелось бы по этому поводу сказать. не всегда надо бездумно подвергать анализу последнюю формулу, особенно когда знаменатель  обращается в ноль.

Источник: https://abakbot.ru/online-10/177-srednyaya-skorost-dvizheniya