Производная функции: основные понятия и определения

Справочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.

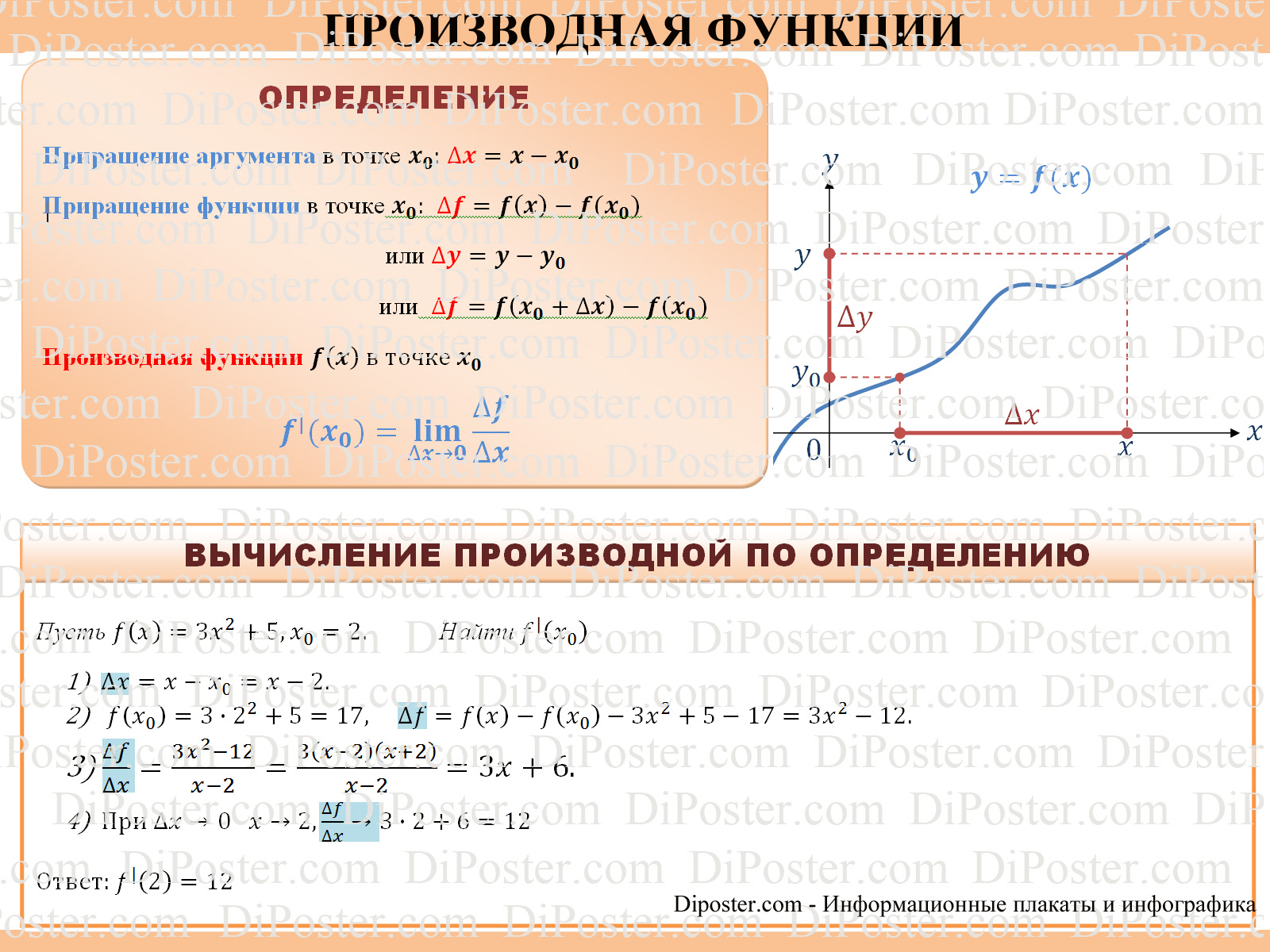
Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть

Таблица производных основных математических функций:

Правила вычисления производных

Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)

Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).

Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).
Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!

Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.

Производная от произведения числа на функцию. Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.

Производная сложной функции:

Ваши комментарии и отзывы к странице с производными:
Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.

Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.

Виртуальный математический справочник.
Колпаков Александр Николаевич, репетитор по математике.

Источник: https://ankolpakov.ru/2010/10/30/proizvodnye-matematicheskix-funkcij-opredelenie-tablica-osnovnyx-proizvodnyx-pravila-ix-vychisleniya/

Производная функции

Елена Репина 2013-08-06 2014-01-11

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует.

Пример: 

Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…

Работу нам упростит таблица производных и правила дифференцирования.

Геометрический смысл производной

• 
• Если мы рассмотрим прямоугольный треугольник , то заметим, что есть .
• А при стремлении к нулю, точка будет приближаться к точке и секущая «превратится» в касательную к графику функции в точке .
• Поэтому геометрический смысл производной таков:
• Производная  в точке  () равна тангенсу угла   наклона   касательной к графику функции в этой точке:
• ,
• где – угол наклона касательной (проведенной  к в т. )

Физический смысл производной

1. Если точка движется вдоль оси и ее координаты изменяются по закону , то мгновенная скорость точки:
2. ,
3. а ускорение:

Пример:

Материальная точка движется прямолинейно по закону , где  — расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .

• Решение:
• м/с
• Ответ: 60.

Уравнение касательной

Уравнение касательной к графику в точке :

Пример:

1. Составить уравнение касательной к графику функции  в точке .
2. Решение:
3. 1.
4. 2.
5. 3.
6. Ответ:
7. Смотрите также  «Производная функции в точке. Знак производной и монотонность функции»

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Источник: https://egemaximum.ru/proizvodnaya-funkcii/

Производная, основные определения и понятия

В этой статье дадим основные понятия, на которых будет базироваться вся дальнейшая теория по теме производная функции одной переменной.

Путь x – аргумент функции f(x) и — малое число, отличное от нуля.

(читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения (отсюда видна суть названия «приращение» аргумента).

При переходе от значения аргумента к значения функции изменяются соответственно от до при условии монотонности функции на отрезке . Разность называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.

Определение производной функции в точке.

Пусть функция f(x) определена на промежутке (a; b), и — точки этого промежутка.Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при . Обозначается .

Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, чтопроизводная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.

Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.

Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке.

Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x) на интервале (a; b).

Операция нахождения производной называется дифференцированием.

Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.

http://www.cleverstudents.ru/derivative/derivative_basic_definitions_and_conceptions.html

Пусть функции и имеют производные в точке . Тогда существуют производные в левых частях следующих равенств и имеют место соотношения:

http://kma.imkn.urfu.ru/Method/math_an_1/modules/part_7.html

Не нашли то, что искали? Воспользуйтесь поиском:

Источник: https://studopedia.ru/5_17903_proizvodnaya-osnovnie-opredeleniya-i-ponyatiya.html

Производная функции. Геометрический смысл производной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

• Вот другой пример.
• Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
• 

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

1. Производная функции обозначается .
2. Покажем, как найти с помощью графика.
3. 

Нарисован график некоторой функции . Возьмем на нем точку  с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

• Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
• Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина  в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

1. .
2. Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке  наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке  производная отрицательна.

• Вот что получается:
• Если функция возрастает, ее производная положительна.
• Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках  (точка максимума) и  (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка  — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке  с «плюса» на «минус».

1. В точке  — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
2. Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
3. Если производная положительна, то функция возрастает.
4. Если производная отрицательная, то функция убывает.
5. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
6. В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
7. Запишем эти выводы в виде таблицы:

возрастает	точка максимума	убывает	точка минимума	возрастает
+		—		+

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке  касательная к графику горизонтальна, и производная равна нулю. Однако до точки  функция возрастала — и после точки  продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.

Источник: https://ege-study.ru/ru/ege/materialy/matematika/proizvodnaya-funkcii-geometricheskij-smysl-proizvodnoj/

4.1.1 Понятие о производной функции, геометрический смысл производной

Видеоурок: Производная и ее геометрический смысл

Лекция: Понятие о производной функции, геометрический смысл производной

Понятие о производной функции

Рассмотрим некоторую функцию f(x), которая будет непрерывной на всем промежутке рассмотрения. На рассматриваемом промежутке выберем точку х0, а также величину функции в данной точке.

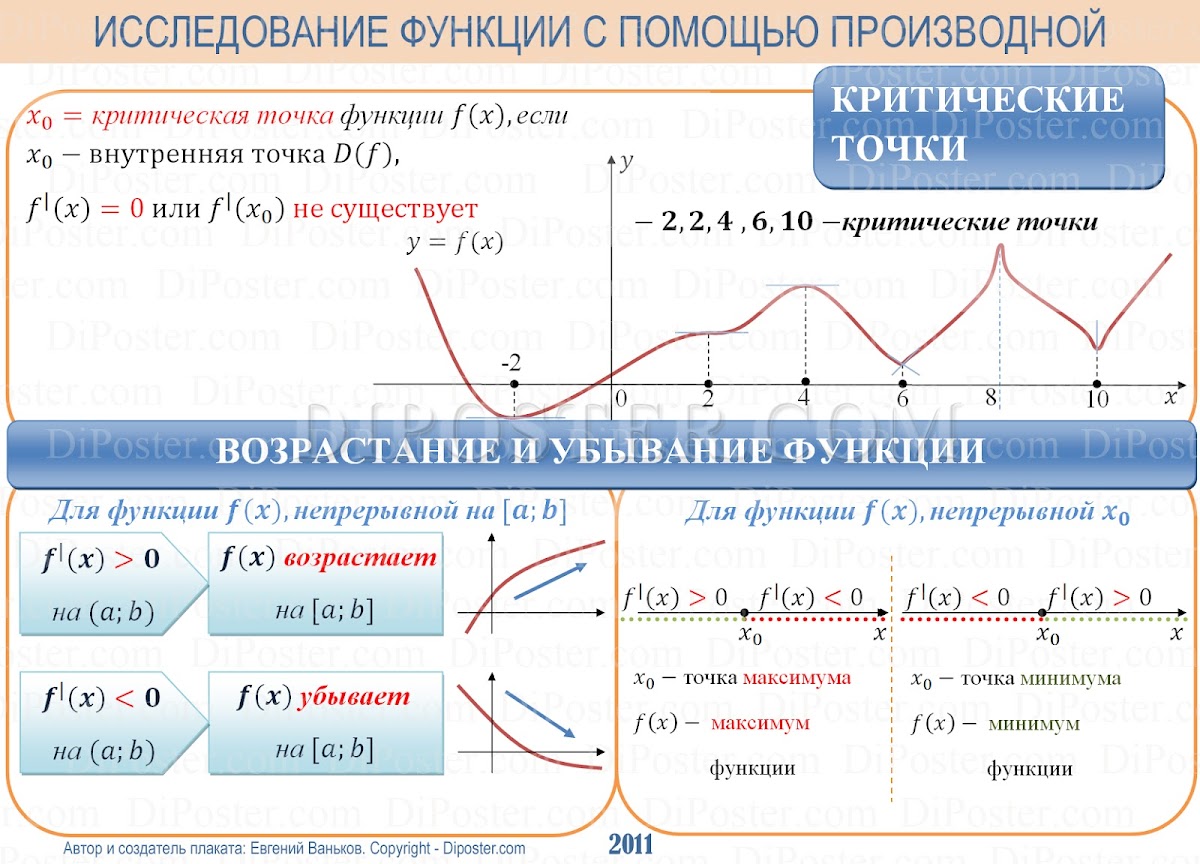
Итак, давайте рассмотрим график, на котором отметим нашу точку х0, а также точку (х0 + ∆х). Напомним, что ∆х – это расстояние (разница) между двумя выбранными точками.

Так же стоит понимать, что каждому х соответствует собственное значение функции у. 

Разница значений функции в точке х0 и (х0 + ∆х) называется приращением данной функции: ∆у = f(х0 + ∆х) — f(х0).

Давайте обратим внимание на дополнительную информацию, которая имеется на графике – это секущая, которая названа КL, а также треугольник, который она образует с интервалами KN и LN.

Угол, под которым находится секущая, называется её углом наклона и обозначается α. Легко можно определить, что градусная мера угла LKN так же равна α.

• А теперь давайте вспомним соотношения в прямоугольном треугольнике tgα = LN / KN = ∆у / ∆х.
• То есть тангенс угла наклона секущей равен отношению приращения функции к приращению аргумента.
• В свое время, производная – это предел отношения приращения функции к приращению аргумента на бесконечно малых интервалах.

Производная определяет скорость, с которой происходит изменение функции на некотором участке.

Геометрический смысл производной

Если найти производную любой функции в некоторой точке, то можно определить угол, под которым будет находится касательная к графику в данной токе, относительно оси ОХ. Обратите внимание на график – угол наклона касательно обозначается буквой φ и определяется коэффициентом k в уравнении прямой: y = kx + b.

То есть можно сделать вывод, что геометрическим смыслом производной является тангенс угла наклона касательной в некоторой точке функции.

Для нахождения производных необходимо пользоваться основными формулами, которые можно найти в таблице производных:

Предыдущий урок

Следующий урок

Источник: https://cknow.ru/knowbase/699-411-ponyatie-o-proizvodnoy-funkcii-geometricheskiy-smysl-proizvodnoy.html

Что такое производная? Понятие производной

Прежде, чем ответить на вопрос как найти производную, необходимо понять что такое производная и, главное, зачем она нужна?

Так вот, производная функции очень важное понятие в науке и имеет огромное значение в прикладных задачах. Говоря о производной, имеют в виду скорость изменения чего-либо, например, движения материальной точки, или скорость распада химических элементов.

Запомните, везде, где протекают неравномерные процессы, производная помогает успешно изучать эти самые процессы.

К слову, с помощью производной решаются задачи оптимизации. Например, оптимизация процессов с целью извлечь максимальную прибыль, или затратить наименьшее количество ресурсов.

С появлением производной стало возможным объяснить научным языком законы природы. Да что там законы природы, производная реально помогает сэкономить деньги. Вы спросите как? Время придёт — увидите!

Немного конкретики

Производная от функции есть новая функция, которая получается по конкретному правилу. Процесс поиска производной называется дифференцированием функции.

• Такие термины как найти производную, решить производную, вычислить производную, взять производную, продифференцировать функцию — означают одно и то же.
• Еще раз повторим, чтобы найти производную от функции, необходимо эту функцию продифференцировать.
• Чтобы безошибочно решать производные, нужно запомнить табличные производные, знать правила дифференцирования и научиться применять их в соответствующих случаях.

И тут возникает резонный вопрос. А как конкретно вычислять производные? По каким таким правилам нужно дифференцировать?

Давайте построим логическую цепочку. С английского языка слово difference переводится как разность. А вот и сама формула для определения производной:

Производная определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Очень важным моментом в понимании производной является то, что производная определяется в некоторой точке области определения функции. Запомните это!

Функцию, имеющую конечную производную в некоторой точке, называют дифференцируемой в данной точке, то есть путем операции дифференцирования, можно получить производную для исходной функции.

Историческая справка

Открытие производной принято считать заслугой Исаака Ньютона. В конце XVII века он установил зависимость скорости от времени и расстояния по следующей формуле: V(t)=S’(t). В этом заключается физический смысл производной

Ученый обнаружил, что подобная взаимосвязь присутствует между множеством различных количественных характеристик, исследуемых физикой, биологией, географией, химией и другими науками.

Наравне с Ньютоном часть открытия основных законов математического анализа принадлежит немецкому математику Лейбницу.

К этим законам Лейбниц пришел, решая задачу проведения касательной к произвольной кривой, т.е. сформулировал геометрический смысл производной

1. Сам термин производная и современные обозначения y’, f’ ввёл Лагранж уже только в 1797 году, спустя столетие с момента ее «зарождения».
2. Применение производной
3. Вычисление производной функции необходимо для решения множества разнообразных задач. Такие задачи используют в своей работе представители различных профессий:

Инженеры-технологи. Деятельность таких специалистов связана с необходимостью организации производства таким образом, чтобы получить возможность выпуска максимально возможного объема продукции.

Конструкторы. При разработке деталей высокоточных механизмов важно правильно рассчитать их массу и другие параметры.

Экономисты. Область деятельности таких специалистов связана с проведением расчетов на транспортные и прочие расходы организации. С помощью специальных формул профессионалы проводят вычисления с целью минимизировать затраты.

• Вычисление производных широко используется в различных дисциплинах.
• Производная в алгебре
• В математике дифференциальное исчисление используется при решении следующих видов задач:
• ● Построение касательной к графику функции

  ● Поиск промежутков возрастания и убывания функции

  ● Поиск точек экстремума функции

  ● Поиск промежутков выпуклости и вогнутости графика функции

  ● Поиск точек изгиба функции

• Производная в физике
• В физике также широко применяется вычисление производных. Чаще всего это необходимо для нахождения следующих величин:
• ● Скорость (находится как производная от расстояния)

  ● Ускорение (производная скорости)

  ● Скорость распада радиоактивных элементов

  ● Скорость материальной точки

  ● Мгновенная скорость

• Производная в химии
• В химии дифференциальное исчисление используется для построения математических моделей химических взаимодействий и изучения их свойств.

При помощи производной можно вычислить скорость химической реакции. Этот показатель является одним из важнейших при решении различных задач и вычислении множества параметров.

1. Также производная необходима для вычисления следующих величин:
2. ● Количество вещества в момент времени

   ● Интервал времени

   ● Изменение количества вещества

   ● Средняя скорость химической реакции

3. Производная в других науках
4. В биологии дифференциальное исчисление используется при изучении популяций.
5. В географии производные позволяют получить следующие данные:
6. ● Некоторые сейсмографические величины

   ● Особенности электромагнитного поля местности

   ● Уровень радиоактивности ядерных и геофизических показателей

   ● Различные показатели в экономической географии

   ● Формула расчета численности населения на территории в определенный момент времени

7. Также дифференциальное исчисление используется для решения различных задач в экономике, электротехнике и многих других дисциплинах.
8. Теперь вы знаете что такое производная функции и откуда она взяла свои истоки.
9. Далее объясним в чём заключается геометрический смысл производной?

Источник: https://math24.biz/article?id=ponyatiye_proizvodnoy