Точки разрыва функции, с примерами

Определение точек разрыва функции и их видов является продолжением темы непрерывности функции. Наглядное (графическое) объяснение смысла точек разрыва функции даётся так же в контрасте с понятием непрерывности.

Научимся находить точки разрыва функции и определять их виды. И помогут нам в этом наши верные друзья — левый и правый пределы, обобщённо называемые односторонними пределами.

Если у кого-то есть страх перед односторонними пределами, то скоро развеем его.

Точки на графике, которые не соединены между собой, называются точками разрыва функции. График такой функции, терпящей разрыв в точке x=2 — — на рисунке ниже.

Обобщением вышесказанного является следующее определение. Если функция не является непрерывной в точке , то она имеет в этой точке разрыв а сама точка называется точкой разрыва. Разрывы бывают первого рода и второго рода.

Для того, чтобы определять виды (характер) точек разрыва функции нужно уверенно находить пределы, поэтому нелишне открыть в новом окне соответствующий урок. Но в связи с точками разрыва у нас появляется кое-что новое и важное — односторонние (левый и правый) пределы. Обобщённо они записываются (правый предел) и (левый предел).

Как и в случае с пределом вообще, для того, чтобы найти предел функции, нужно в выражение функции вместо икса подставить то, к чему стремится икс.

Но, возможно, спросите вы, чем же будут отличаться правый и левый пределы, если в случае правого к иксу хотя что-то и прибавляется, но это что-то — ноль, а в случае левого из икса что-то вычитается, но это что-то — тоже ноль? И будете правы. В большинстве случаев.

Но в практике поиска точек разрыва функции и определения их вида существует два типичных случая, когда правый и левый пределы не равны:

• у функции существует два или более выражений, зависящих от участка числовой прямой, к которой принадлежит икс (эти выражения обычно записываются в фигурных скобках после f(x)=);
• в результате подстановки того, к чему стремится икс, получается дробь, в знаменателе которой остаётся или плюс ноль (+0) или минус ноль (-0) и поэтому такая дробь означает либо плюс бесконечность, либо минус бесконечность, а это совсем разные вещи.

Точка разрыва первого рода: у функции существуют как конечный (т. е. не равный бесконечности) левый предел, так и конечный правый предел, но функция не определена в точке или левый и правый пределы различны (не равны).

Точка устранимого разрыва первого рода. Левый и правый пределы равны. При этом существует возможность доопределить функцию в точке.

Доопределить функцию в точке, говоря просто, значит обеспечить соединение точек, между которыми находится точка, в которой найдены равные друг другу левый и правый пределы.

При этом соединение должно представлять собой лишь одну точку, в которой должно быть найдено значение функции.

Пример 1. Определить точку разрыва функции и вид (характер) точки разрыва.

Решение. Функция не определена в точке . Находим левый и правый пределы функции в этой точке:

• ,
• .
• Левый и правый пределы равны, следовательно точка — точка устранимого разрыва первого рода.
• Есть возможность доопределить функцию:

График функции с точкой разрыва — под примером.

Точка неустранимого (конечного) разрыва первого рода. Существуют левый и правый пределы, но они различны (не равны). Функцию невозможно доопределить. Разность пределов называется скачком.

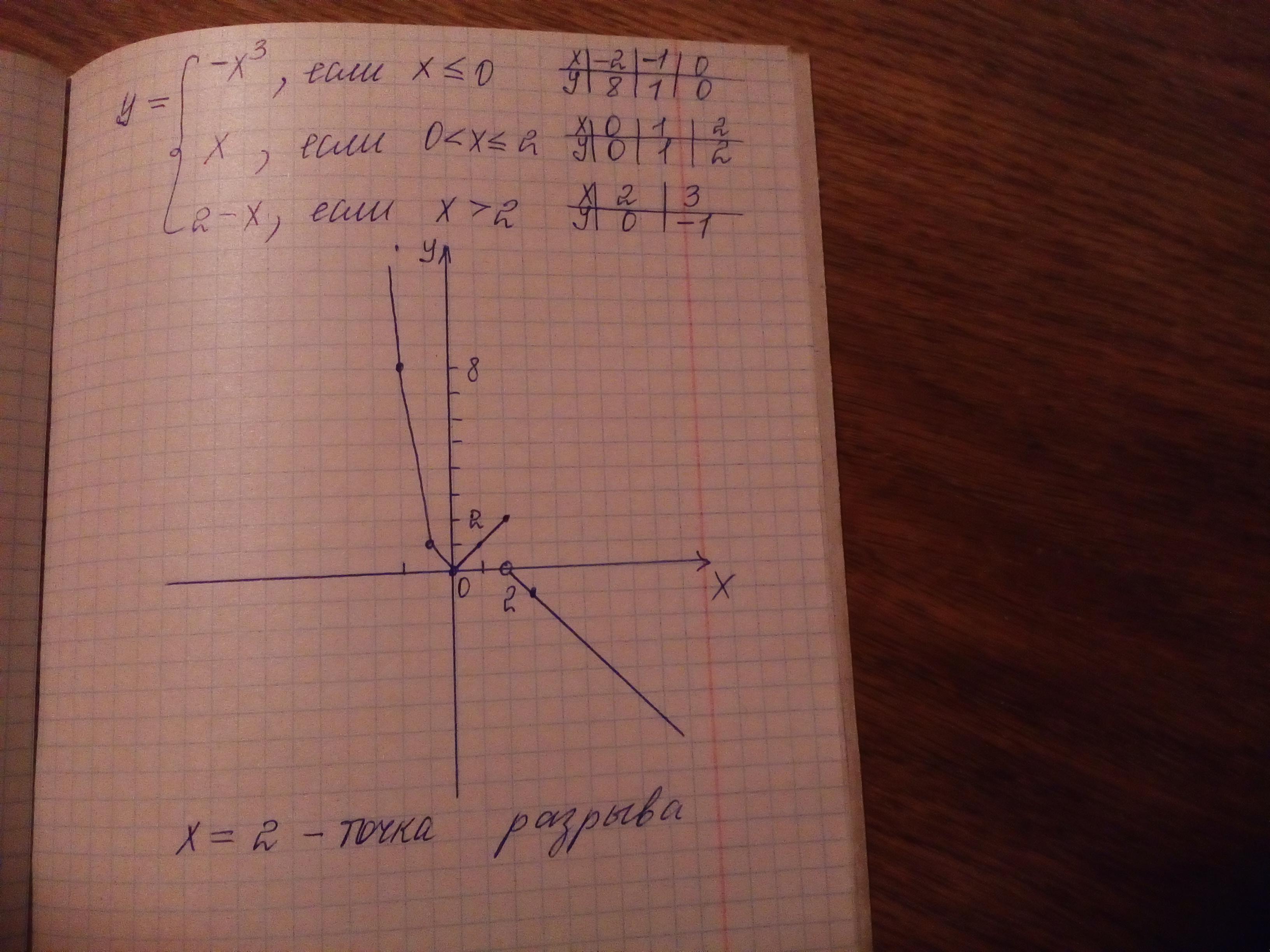
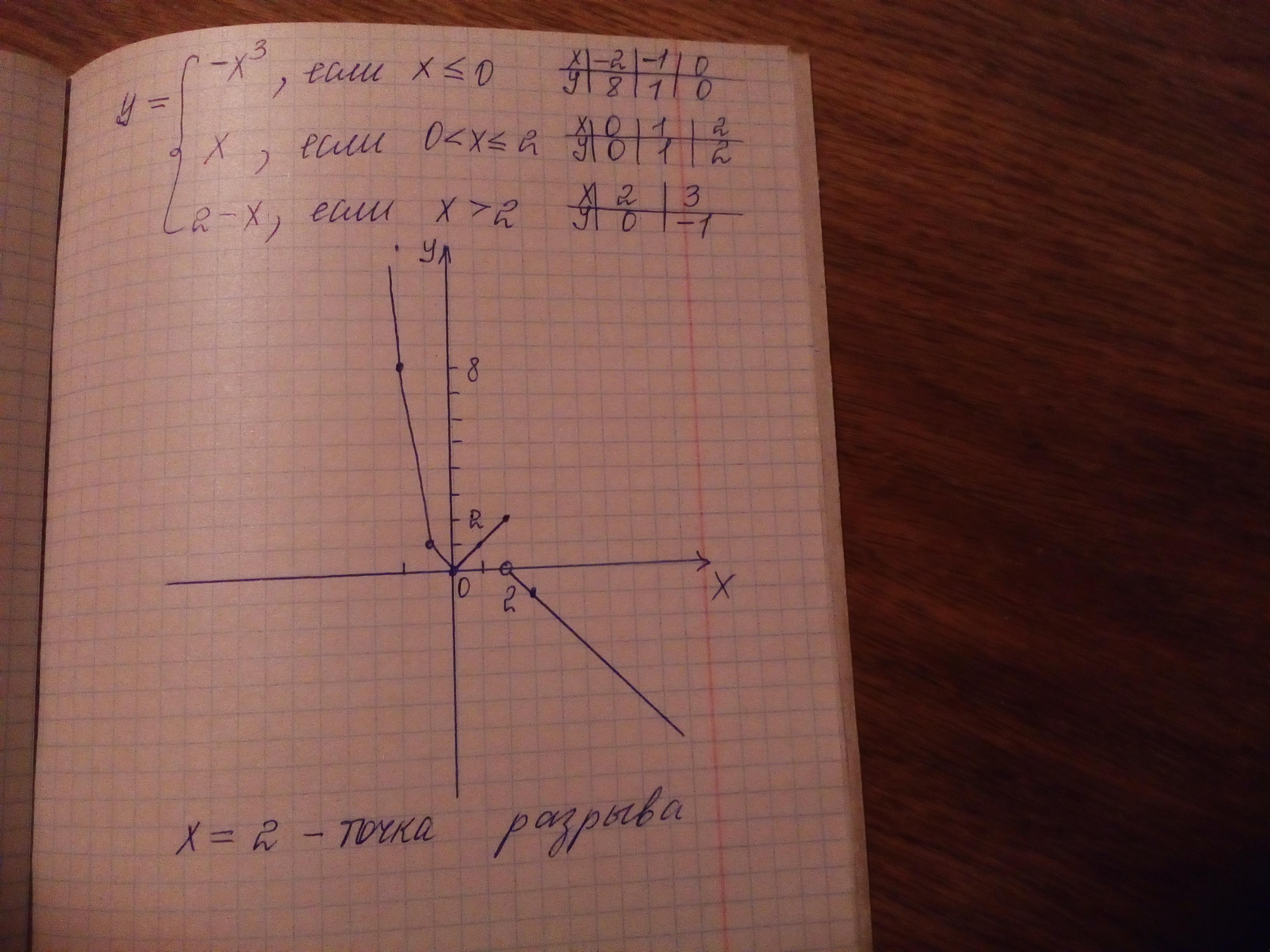
Пример 2. Определить точку разрыва функции и вид (характер) точки разрыва для функции

Решение. Очевидно, что в точке меняется выражение функции. Найдём левый и правый пределы функции в этой точке:

,

.

Левый и правый пределы не равны равны, следовательно точка — точка неустранимого (конечного) разрыва первого рода. График функции с точкой разрыва — под примером.

Нахождение точек разрыва функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Производная, дифференциал и их применение

Пройти тест по теме Предел

Точки разрыва второго рода

Точка разрыва второго рода: точка, в которой хотя бы один из пределов (левый или правый) — бесконечный (равен бесконечности).

Пример 3. Определить точку разрыва функции и вид (характер) точки разрыва для функции

Решение. Из выражения степени при e видно, что в точке функция не определена. Найдём левый и правый пределы функции в этой точке:

Один из пределов равен бесконечности, поэтому точка — точка разрыва второго рода. График функции с точкой разрыва — под примером.

Нахождение точек разрыва функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.

И ещё пара примеров, решаемых вместе, а далее — для самостоятельного решения.

Пример 4. Определить точку разрыва функции и вид (характер) точки разрыва для функции

Решение. Из выражения степени при 2 видно, что в точке функция не определена. Найдём левый и правый пределы функции в этой точке:

Пределы не равны и конечны, поэтому точка — точка неустранимого разрыва первого рода. График функции с точкой разрыва — под примером.

Пример 5. Определить точку разрыва функции и вид (характер) точки разрыва для функции

Решение. Очевидно, что в точке функция не определена. Найдём левый и правый пределы функции в этой точке:

,

.

Оба предела бесконечны, поэтому точка — точка разрыва второго рода. График функции с точкой разрыва — под примером.

Решить задачи на точки разрыва самостоятельно, а затем посмотреть решение

Пройти тест по теме Предел

Весь раздел «Исследование функций»

Источник: https://function-x.ru/function_discontinuity.html

[Зачет 81] Непрерывность функции в точке. Точки разрыва и их классификация. Скачок. Вертикальные асимптоты

Непрерывность функции в точке. 

Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).

Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:

f(x) = f(x0),

(1)

т.е.

» O( f(x0) )     $ O(x0) :     x О O(x0) Ю f(x) О O( f(x0) ) .

Точки разрыва и их классификация. 

       Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

      Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

• Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
• 
• не является непрерывной в любой точке х0.

Пример. Функция f(x) =  имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.

.

Скачок.

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции.

Вертикальные асимптоты. 

Если хотя бы один из односторонних пределов f(x0 − 0),  f (x0 + 0) равен бесконечности, то прямая x = x 0 называется вертикальной асимптотой графика функции y = f(x).

 Вертикальные асимптоты 

     1. Линия задана уравнением y = f(x). Если , то x = a — вертикальная асимптота. В частности, если , то x = a — вертикальная правосторонняя асимптота; если же , то x = a — вертикальная левосторонняя асимптота.

     2. Линия задана уравнениями x = x(t), y = y(t). Если , , то x = a — вертикальная асимптота. В частности, если , , то x = a — вертикальная правосторонняя асимптота; если же , , то x = a — вертикальная левосторонняя асимптота.

Источник: http://fizmatinf.blogspot.com/2013/05/81.html

Точки разрыва функции первого и второго рода

Функция f(x) называется непрерывной в точке х = а если: 1) она определена в этой точке; 2) существует предел функции в этой точке

3) значение предела равно значению функции в точке х = а, т.е.

Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.

Классификация точек разрыва

Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа и слева

• Если, кроме этого, выполняется хотя бы одно из условий то функция в точке х = а имеет неустранимый разрыв первого рода.
• Если пределы равны, однако функция не существует то имеем устранимый разрыв первого рода.
• Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа или слева не существует или бесконечна.
• Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ если они разные и не равны бесконечности.
• При нахождении точек разрыва функции можно руководствоваться следующими правилами:

1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале. 2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки. 3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.

1. Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.
2. Рассмотрим несколько задач по данной теме.
3. Задача 1. Найти точки разрыва функции а)
4. Решение: Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая
5. Найдем односторонние пределы в точках разрыва

При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.

• Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы являются точками разрыва второго рода. График функции приведен на рисунке ниже
• ——————————————————-
• б)
• Решение: Задача достаточно простая. В первую очередь находим нули знаменателя
• Таким образом функция определена на всей действительной оси за исключением точек , которые являются точками разрыва. Вычислим односторонние пределы справа и слева
• Пределы бесконечны поэтому, по определению, имеем точки разрыва второго рода.

Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.

1. ——————————————————-
2. в)
3. Решение: Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке

Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.

——————————————————-

Задача 2. Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.

• а)
• Решение: Для заданной функции точка x = 2 является точкой разрыва. Найдем предел функции , чтобы определить характер разрыва
• По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2
• График функции на интервале который нас интересует приведен далее
• ——————————————————-
• б)

Решение: Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы

1. Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция — непрерывная.
2. Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.
3. Исследуем на непрерывность вторую точку
4. По определению функция в точке x = 2 имеет неустранимый разрыв І рода.
5. Прыжок функции равен 29 — (- 3) = 31.
6. По условию задания построим график функции.

Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.

Источник: https://yukhym.com/ru/issledovanie-funktsii/tochki-razryva-funktsii.html

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел и правосторонний предел ;
• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Пример 1

Решение.

Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.

Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода.

Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.

• Пример 2
• Показать, что функция имеет устранимый разрыв в точке x = 0.
• Решение.

Очевидно, данная функция не определена при x = 0. Поскольку sin x является непрерывной функцией для всехx, то искомая функция также непрерывна при всех x за исключением точки x = 0. Так как , то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию

1. которая будет непрерывной при любом действительном x.
2. Пример 3
3. Найти точки разрыва функции , если они существуют.
4. Решение.

Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем «поведение» этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется.

• Вычислим односторонние пределеы при x = 0.
• Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен
• При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва.
• Пример 4
• Найти точки разрыва функции , если они существуют.
• Решение.

Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке.

Видно, что в точке x = 0 существует разрыв первого рода (рисунок 2).

Рис.2

Рис.3

1. Пример 5
2. Найти точки разрыва функции , если таковые существуют.
3. Решение.

Функция определена и непрерывна при всех x, за исключением точки , где существует разрыв. Исследуем точку разрыва.

Так как значения односторонних пределов конечны, то, следовательно, в точке существует разрыв первого рода. График функции схематически показан на рисунке 3.

42.

43.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) — немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке выполняется условие — .

Свойство 2: Функция, непрерывная на отрезке , принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения и , что , причем .

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например — ).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано — Коши). Функция, непрерывная на отрезке , принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция непрерывна в точке , то существует некоторая окрестность точки , в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) — Коши). Если функция — непрерывная на отрезке и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где .

Т.е. если , то .

Определение. Функция называется равномерно непрерывной на отрезке , если для любого существует такое, что для любых точек и таких, что верно неравенство .

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) — немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Свойство 7: Если функция определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция тоже однозначна, монотонна и непрерывна.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть. в точке функция непрерывна в точке

точка разрыва 1 — го рода

Источник: https://megaobuchalka.ru/7/30562.html

Как найти точки разрыва функции — пошаговая инструкция

Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.

Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.

Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.

Определение точки разрыва

Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:

Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:

Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.

К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.

Классификация точек разрыва.

Точки разрыва первого и второго рода

Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:

• Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.
• Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно. Разница первого и второго называется скачком.
• Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.

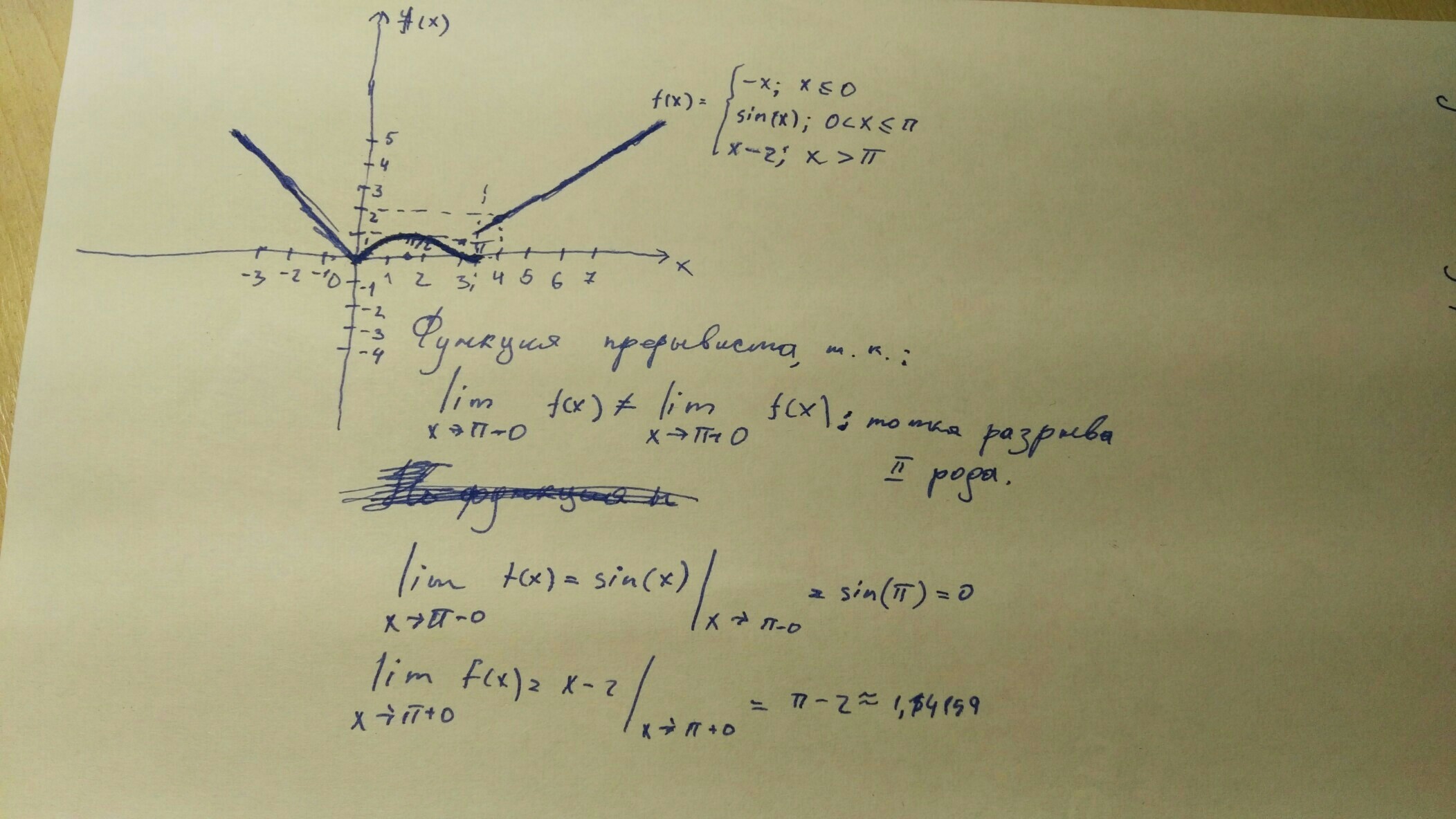
Как найти точки разрыва функции

Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.

Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² — 25)/(y — 5):

1. Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
2. Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
3. Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.

Видео

Из этого видео вы узнаете, как исследовать непрерывность функции.

Источник: https://LivePosts.ru/articles/education-articles/matematika/kak-najti-tochki-razryva-funktsii-poshagovaya-instruktsiya