Число е: определение, значение и примеры

Число e

Теорема. Последовательность с общим членом    имеет конечный предел при  . Замечание. Для обозначения этого предела используется символ e: Число  e  является иррациональным, приближенное значение которого равно e = 2.71828182845904523536028747135266249775724709… Доказательство. Покажем сначала, что    представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона, Полагая  , получим Аналогично, Сравним выражения для    и  . Во-первых, оба эти выражения содержат только положительные слагаемые. Во-вторых, начиная со второго слагаемого, каждый член в выражении для    превышает соответствующий член выражения для  , поскольку В-третьих, выражение для    состоит из большего числа слагаемых. Следовательно,   Далее докажем, что последовательность    является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом,    для всех натуральных значений  n.Перейдем к доказательству существования верхней границы. Очевидно, что Кроме того,    для всех  k > 3. Тогда Правая часть этого неравенства представляет собой сумму членов убывающей геометрической прогрессии. В качестве верхней границы этой суммы выступает любое число  . Таким образом, последовательность с общим членом представляет собой ограниченную монотонно возрастающую последовательность и, следовательно, имеет конечный предел – согласно теореме о монотонных последовательностях.

Источник: http://portal.tpu.ru/SHARED/k/KONVAL/Sites/Russian_sites/Calc1-ru/1/09.htm

Математика, которая мне нравится

Число впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел.

Однако никто не понял, что это логарифмы по основанию , так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число.

Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется , но опять-таки завуалированно.

Следующее появление числа снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу . Только к 1661 г.

Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы равнобочной гиперболы на промежутке от до равна .

Это свойство делает основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.

Гюйгенс сделал следующий шаг в 1661 г. Он определил кривую, которую назвал логарифмической (в нашей терминологии мы будем называть ее экспоненциальной). Это кривая вида .

И снова появляется десятичный логарифм , который Гюйгенс находит с точностью до 17 десятичных цифр.

Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к , но само число остается неузнанным).

В дальнейших работах по логарифмам опять-таки число не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г.

В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию . Число явно опять не появляется, а остается неуловимым где-то в стороне.

Удивительно, что число в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти

   

Он использует биномиальную теорему для доказательства того, что этот предел находится между и , и это мы можем рассматривать как первое приближение числа . Хотя мы принимаем это за определение , это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.

Ранее упоминалось, что логарифмы в начале их изучения никак не связывались с экспонентами. Конечно, из уравнения мы находим, что , но это гораздо более поздний способ восприятия.

Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной.

С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.

Мы знаем, что число появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение . Наконец у появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.

В 1697 г. Иоганн Бернулли начинает изучение показательной функции и публикует Principia calculi exponentialum seu percurrentium. В этой работе вычисляются суммы различных экспоненциальных рядов, и получены некоторые результаты их почленным интегрированием.

Эйлер (Euler) ввел так много математических обозначений, что
неудивительно, что обозначение также принадлежит ему. Кажется смешным утверждение, что он использовал букву из-за того, что это первая буква его имени.

Вероятно, это даже не потому, что взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г.

Он сделал много открытий, изучая в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с . Он показал, что

•    
• Эйлер также нашел первые 18 десятичных знаков числа :
•    

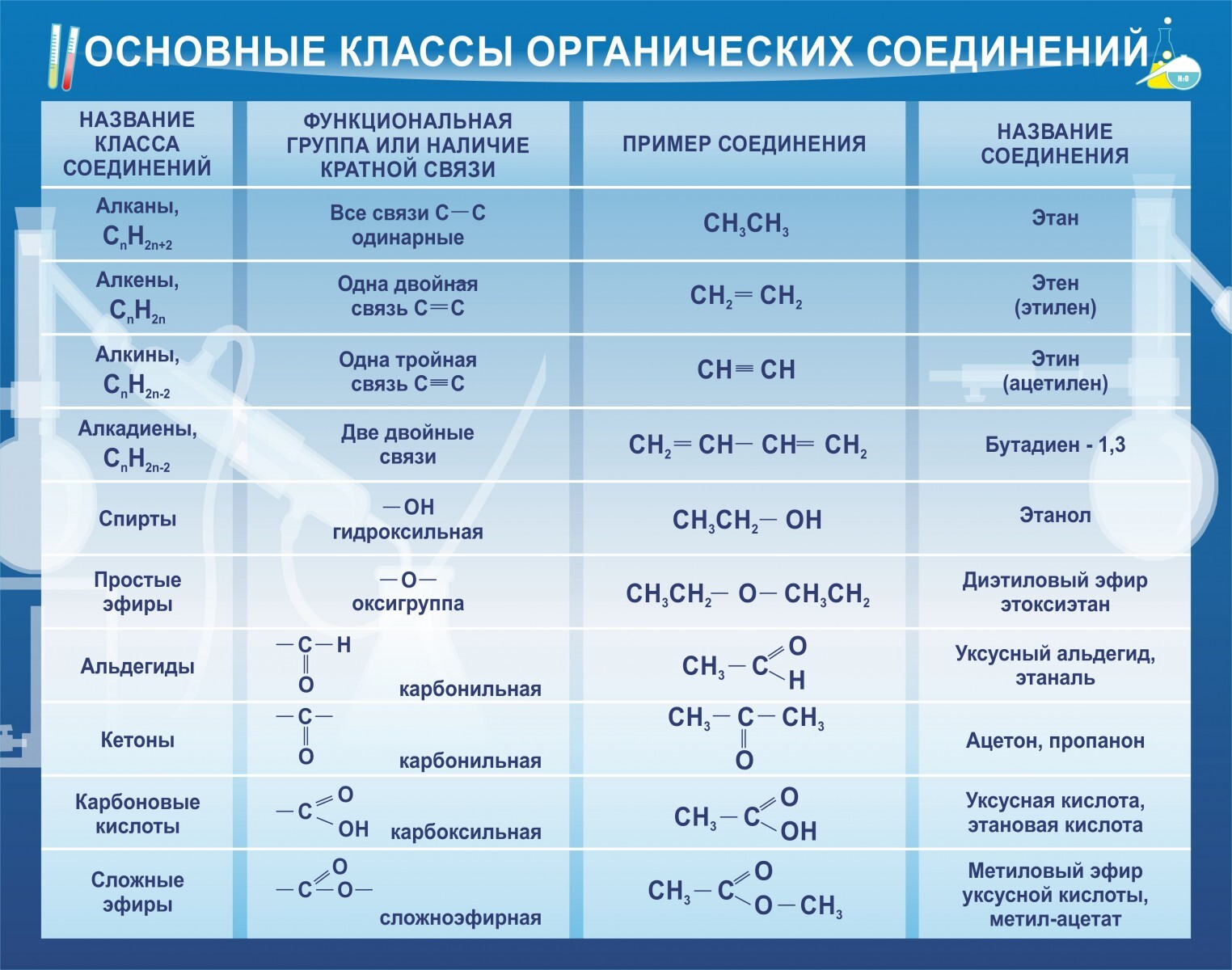
правда, не объясняя, как он их получил. Похоже, что он вычислил это значение сам. На самом деле, если взять около 20 членов ряда (1), то получится точность, которую получил Эйлер. Среди других интересных результатов в его работе приведена связь между функциями синус и косинус и комплексной показательной функцией, которую Эйлер вывел из формулы Муавра.

Интересно, что Эйлер нашел даже разложение числа в непрерывные дроби и привел образцы такого разложения. В частности, он получил
и
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность . Действительно, если бы непрерывная дробь для продолжалась так же, как в приведенном образце, (каждый раз прибавляем по ), то она никогда бы не прервалась, и (а значит, и ) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность .

Первым, кто вычислил довольно большое число десятичных знаков числа , был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа . В действительности, нужно около
120 членов разложения (1), чтобы получить 200 верных знаков числа .

1. В 1864 г. Бенджамен Пирс (Peirce) стоял у доски, на которой было написано
2. В своих лекциях он мог бы сказать своим студентам: “Джентльмены, мы не имеем ни малейшего представления, что бы это значило, но мы можем быть уверены, что это значит что-то очень важное”.

Большинство считает, что Эйлер доказал иррациональность числа . Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел и является трансцендентным.

Далее вычисляли следующие десятичные знаки числа . В 1884 г. Бурман (Boorman) вычислил 346 знаков числа , из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма .

J.J.Connor, E.F.Robertson. The number e. Перевод статьи http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/e.html

Источник: http://hijos.ru/2010/10/09/chislo-e/

«Популярное изложение»: Число Эйлера и наши финансы. Краткое знакомство с константой «е»

Число «е» – одна из важнейших математических констант, о которой каждый слышал на школьных уроках математики. Concepture публикует популярное изложение, написанное гуманитарием для гуманитариев, в котором доступным языком расскажет зачем и почему существует число Эйлера.

В то время как у числа π (пи) есть вполне определенный геометрический смысл и его использовали еще древние математики, то число е (число Эйлера) заняло свое заслуженное место в науке сравнительно недавно и корни его уходят прямиком… к финансовым вопросам.

С момента изобретения денег прошло совсем немного времени, когда люди догадались, что валюту можно одалживать или ссужать под определенный процент. Естественно, «древние» бизнесмены не пользовались привычным нам понятием «процент», но увеличение суммы на какой-то определенный показатель за установленный период времени было им знакомо.

На фото: банкнота стоимостью 10 франков с изображением Леонарда Эйлера (1707-1783).

Пытаясь высчитать, за сколько времени сумма, одолженная, допустим, под 20% годовых увеличится вдвое, люди уже начинали наощупь отыскивать путь, который в конечном итоге привел к определению числа е.

Мы не будем углубляться в пример с 20% годовых, так как от него добираться до числа Эйлера слишком долго. Воспользуемся самым распространенным и наглядным объяснением значения этой константы, а для этого нам придется немного пофантазировать и вообразить, что какой-то банк предлагает нам положить деньги на депозит под 100% годовых.

Мысленно-финансовый эксперимент

Для этого мысленного эксперимента можно взять любую сумму и результат всегда будет идентичным, но именно начиная с 1, мы сможем прийти непосредственно к первому приближенному значению числа е. Потому, допустим, что мы вкладываем в банк 1 доллар, при ставке 100% годовых в конце года у нас будет 2 доллара.

Но это только если проценты капитализируются (прибавляются) раз в год. А что если они будут капитализироваться два раза в год? То есть будет начисляться по 50% каждые полгода, причем вторые 50% будут начисляться уже не от начальной суммы, а от суммы, увеличенной на первые 50%. Будет ли это выгоднее для нас?

Наглядная инфографика, отображающая геометрический смысл числа π.

Разумеется, будет. При капитализации два раза в год, спустя полгода у нас будет 1,50 доллара на счете. К концу года прибавится еще 50% от 1,50 доллара, то есть общая сумма составит 2,25 доллара. Что же будет, если капитализацию проводить каждый месяц?

Нам будут начислять по 100/12% (то есть, примерно по 8,(3)%) каждый месяц, что окажется еще более выгодным – к концу года у нас будет 2,61 доллара. Общая формула для вычисления итоговой суммы при произвольном количестве капитализаций (n) в год выглядит так:

Получается, при значении n = 365 (то есть, если наши проценты будут капитализироваться каждый день), мы получим вот такую формулу: 1(1+1/365)365 = 2,71 доллара.

Из учебников и справочников мы знаем, что е приблизительно равно 2,71828, то есть, рассматривая ежедневную капитализацию нашего сказочного вклада мы уже подошли к приблизительному значению е, которое уже достаточно для многих вычислений.

Рост n можно продолжать бесконечно и чем больше будет его значение, тем точнее мы сможем вычислить число Эйлера, вплоть до необходимого нам, по какой-либо причине, знака после запятой.

Получается, число е что-то вроде меры всех изменений и «натуральный язык математического анализа». Ведь «матан» крепко повязан с понятиями дифференцирования и интегрирования, а обе эти операции имеют дело с бесконечно малыми изменениями, которые так великолепно характеризует число е.

Уникальные свойства числа Эйлера

Рассмотрев самый доходчивый пример объяснения построения одной из формул для вычисления числа е, кратко рассмотрим еще пару вопросов, которые к нему напрямую относятся. И один из них: что же такого уникального в числе Эйлера?

По идее, абсолютно любая математическая константа уникальна и у каждой есть своя история, но, согласитесь, претензия на звание натурального языка математического анализа – довольно весомая претензия.

Первая тысяча значений ϕ (n) для функции Эйлера.

Однако, у числа е есть на то основания. При построении графика функции y = ex выясняется поразительный факт: не только y равен ex, этому же показателю равен градиент кривой и площадь под кривой. То есть площадь под кривой от определенного значения y до минус бесконечности.

Никакое другое число этим похвастаться не может. Нам, гуманитариям (ну, или просто НЕ математикам), такое заявление мало что говорит, но сами математики утверждают, что это очень важно. Почему важно? Мы попробуем разобраться в этом вопросе в другой раз.

Логарифм, как предпосылка Числа Эйлера

Возможно, кто-то помнит со школы, что число Эйлера – это также основание натурального логарифма. Что ж, это согласуется с его природой, как меры всех изменений. Все-таки, причем же тут Эйлер? Справедливости ради нужно отметить, что е также иногда называется числом Непера, но без Эйлера история будет неполной, как и без упоминания о логарифмах.

Изобретение в XVII веке логарифмов шотландским математиком Джоном Непером стало одним из важнейших событий истории математики. На праздновании в честь юбилея этого события, которое прошло в 1914 году Лорд Мултон (Lord Moulton) так отозвался о нем:

«Изобретение логарифмов было для научного мира как гром среди ясного неба. Никакая предшествующая работа не вела к нему, не предсказывала и не обещала это открытие. Оно стоит особняком, оно прорывается из человеческой мысли внезапно, не заимствуя ничего из работы других разумов и не следуя уже известным тогда направлениям математической мысли».

Пьер-Симон Лаплас, знаменитый французский математик и астроном, еще более драматично выразил важность этого открытия: «Изобретение логарифмов, уменьшив часы кропотливого труда, вдвое увеличило жизнь астронома». Что же так впечатлило Лапласа? А причина очень проста – логарифмы позволили ученым в разы уменьшить время, обычно затрачиваемое для громоздких вычислений.

В общем и целом, логарифмы упрощали вычисления – опускали их на один уровень ниже по шкале сложности. Проще говоря, вместо умножения и деления приходилось совершать операции сложения и вычитания. А это намного эффективнее.

е – основание натурального логарифма

Давайте примем за данность тот факт, что Непер был первопроходцем в сфере логарифмов – их изобретателем. По крайней мере, он опубликовал свои открытия первым. В таком случае возникает вопрос: в чем заслуга Эйлера?

Все просто – его можно назвать идейным наследником Непера и человеком, который довел дело жизни шотландского ученного до логарифмического (читать логического) завершения. Интересное такое вообще возможно?

Какой-то очень важный график построенный при помощи натурального логорифма.

Если говорить конкретнее, то Эйлер вывел основание натурального логарифма, теперь известное как число е или число Эйлера. Кроме этого, он вписал свое имя в историю науки столько раз, сколько и не снилось Васе, который, кажется, успел «побывать» везде.

К сожалению, конкретно принципы работы с логарифмами – это тема отдельной большой статьи. Поэтому пока будет достаточно сказать, что благодаря работе ряда самоотверженных ученых, которые, буквально, посвятили годы своей жизни составлению логарифмических таблиц в те времена, когда никто и слыхом не слыхивал о калькуляторах, прогресс науки сильно ускорился.

На фото: Джон Непер — шотландский математик, изобретатель логарифма (1550—1617.)

Забавно, но этот прогресс, в конце концов, привел к выходу из употребления данных таблиц, а причиной тому послужило именно появление ручных калькуляторов, которые полностью переняли на себя задачу по выполнению такого рода вычислений.

Возможно, вы еще слышали о логарифмических линейках? Когда-то без них инженерам или математикам бывало не обойтись, а сейчас это почти как астролябия – интересный инструмент, но скорее в плане истории науки, чем повседневной практики.

Почему так важно быть основанием логарифма?

Оказывается, основанием логарифма может быть любое число (например, 2 или 10), но, именно благодаря уникальным свойствам числа Эйлера логарифм по основанию е называется натуральным. Он как бы встроен в структуру реальности – от него никуда не убежать, да и не нужно, ведь он значительно упрощает жизнь ученым, работающим в самых разных областях.

Приведем доходчивое объяснение природы логарифма с сайта Павла Бердова. Логарифм по основанию a от аргумента x – это степень, в которую надо возвести число a, чтобы получить число x. Графически это обозначается так:

Выше мы видели число 2 в образе основания логарифма, но математики говорят, что самый талантливый актер на эту роль – число Эйлера. Поверим им на слово… А потом проверим, чтобы убедиться самим.

Выводы

Наверное, плохо, что в рамках высшего образования так сильно разделены естественные и гуманитарные науки. Иногда это приводит к слишком сильному «перекосу» и получается так, что с человеком, прекрасно разбирающимся, допустим, в физике и математике, абсолютно неинтересно говорить на другие темы.

И наоборот, можно быть первоклассным специалистом-литературоведом, но, в то же время, быть совершенно беспомощным, когда речь заходит о той же физике и математике. А ведь все науки интересны по-своему.

• Надеемся, что мы, пытаясь преодолеть свою собственную ограниченность в рамках импровизированной программы «я – гуманитарий, но я лечусь», помогли и вам узнать и, главное, понять, что-то новое из не совсем привычной научной сферы.
• Ну а тем, кто захочет поподробнее узнать о числе Эйлера, можем порекомендовать несколько источников, в которых может при желании разобраться даже далекий от математики человек: Эли Маор в своей книге «е: история одного числа» («e: the story of a number») подробно и доступно описывает предысторию и историю числа Эйлера.
• Также, в разделе «Рекомендуем« под этой статьей Вы сможете название youtube-каналов и видео, которые были сняты профессиональными математиками, пытающимися доходчиво объяснить число Эйлера так, чтобы это было понятно даже не специалистам Русские субтитры в наличие. 

1. Eli Maor – «e: the story of a number»
2. Канал «Mathologer» – «The number e explained»
3. Канал «Numberphile» – «Euler's Number»

Источник: https://concepture.club/post/nauka/vse-chto-nuzhno-znat-o-konstante-e

Число е

ЧИСЛО e. Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e–kt, где k – число, характеризующее скорость распада данного вещества.

Обратная величина 1/k называется средним временем жизни атома данного вещества, так как в среднем атом прежде, чем распасться, существует в течение времени 1/k. Величина 0,693/k называется периодом полураспада радиоактивного вещества, т.е.

временем, за которое распадается половина исходного количества вещества; число 0,693 приближенно равно loge 2, т.е. логарифму числа 2 по основанию e.

Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени t начальное количество бактерий N превращается в Nekt.

Число 1/k часто называют временем релаксации. В статистике величина e–kt встречается как вероятность того, что за время t не произошло событий, наступающих случайно со средней частотой k событий в единицу времени. Если S – сумма денег, вложенных под r процентов с непрерывным начислением вместо начисления через дискретные промежутки времени, то к моменту времени t первоначальная сумма возрастет до Setr/100.

Причина «вездесущности» числа e заключается в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию e, а не 10 или какому-либо другому основанию.

Например, производная от log10 x равна (1/x)log10 e, тогда как производная от loge x равна просто 1/x. Аналогично, производная от 2x равна 2xloge 2, тогда как производная от eх равна просто ex.

Это означает, что число e можно определить как основание b, при котором график функции y = logb x имеет в точке x = 1 касательную с угловым коэффициентом, равным 1, или при котором кривая y = bx имеет в x = 0 касательную с угловым коэффициентом, равным 1.

Логарифмы по основанию e называются «натуральными» и обозначаются ln x. Иногда их также называют «неперовыми», что неверно, так как в действительности Дж.Непер (1550–1617) изобрел логарифмы с другим основанием: неперов логарифм числа x равен 107 log1/e (x/107) (см. также ЛОГАРИФМ).

• Различные комбинации степеней e встречаются в математике так часто, что имеют специальные названия. Таковы, например, гиперболические функции
• 
• График функции y = ch x называется цепной линией; такую форму имеет подвешенная за концы тяжелая нерастяжимая нить или цепь. Формулы Эйлера
• 

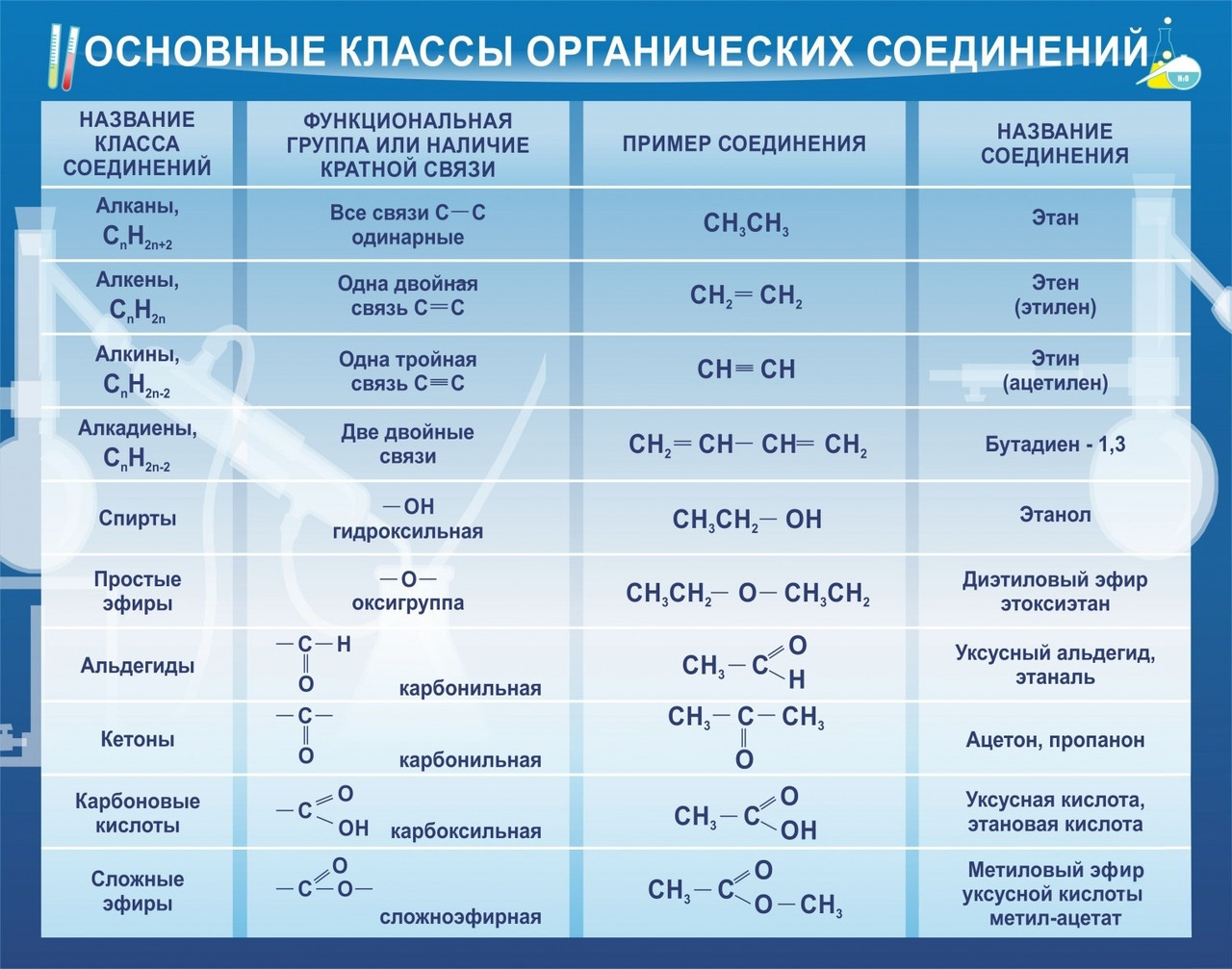
где i2 = –1, связывают число e с тригонометрией. Частный случай x = p приводит к знаменитому соотношению eip + 1 = 0, связывающему 5 наиболее известных в математике чисел.

1. При вычислении значения e могут быть использованы и некоторые другие формулы (чаще всего пользуются первой из них):
2. 
3. 

Значение e с 15 десятичными знаками равно 2,718281828459045. В 1953 было вычислено значение e с 3333 десятичными знаками. Символ e для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783).

Десятичное разложение числа e непериодично (e – иррациональное число). Кроме того, e, как и p, – трансцендентное число (оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами). Это доказал в 1873 Ш.Эрмит. Впервые было показано, что столь естественным образом возникающее в математике число является трансцендентным.

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Источник: https://www.krugosvet.ru/enc/matematika/chislo-e

Экспонента и число е: просто и понятно

Перевод большой статьи «An Intuitive Guide To Exponential Functions & e»

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные.

Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей.

Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д.

Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Понятие экспоненциального роста

Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:

• Бактерии делятся и «удваиваются» в количестве каждые 24 часа
• Мы получаем вдвое больше лапшинок, если разламываем их пополам
• Ваши деньги каждый год увеличиваются вдвое, если вы получаете 100% прибыли (везунчик!)

И выглядит это примерно так:

Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.

Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:

• рост = 2x
• Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
• рост = (1+100%)x

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

1. Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
2. рост = (1+прирост)x
3. Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.

Продолжение

Источник: https://zero2hero.org/article/math/34-eksponenta-i-chislo-e-pros

Числа π и e

Все знают геометрический смысл числа π — это длина окружности с единичным диаметром:

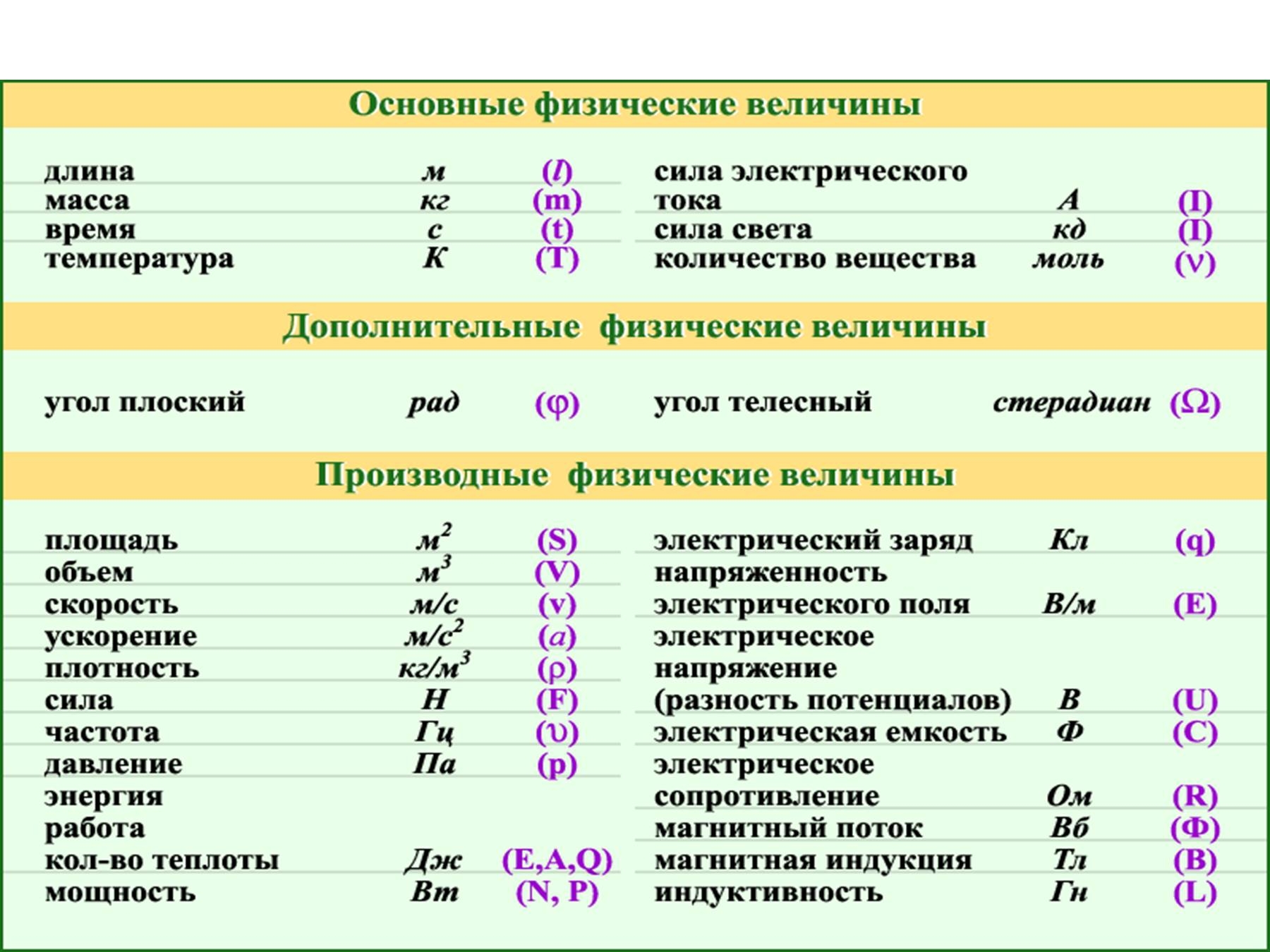
А вот смысл другой важной константы, e, имеет свойство быстро забываться. То есть, не знаю, как вам, а мне каждый раз стоит усилий вспомнить, чем же так замечательно это число, равное 2,7182818284590… (значение я, однако, по памяти записал). Поэтому я решил написать заметку, чтобы больше из памяти не вылетало.

Число e по определению — предел функции y = (1 + 1 / x)x при x → ∞:

x	y
1	(1 + 1 / 1)1	= 2
2	(1 + 1 / 2)2	= 2,25
3	(1 + 1 / 3)3	= 2,3703703702…
10	(1 + 1 / 10)10	= 2,5937424601…
100	(1 + 1 / 100)100	= 2,7048138294…
1000	(1 + 1 / 1000)1000	= 2,7169239322…
∞	lim× → ∞	= 2,7182818284590…

Это определение, к сожалению, не наглядно. Непонятно, чем замечателен этот предел (несмотря на то, что он называется «вторым замечательным»). Подумаешь, взяли какую-то неуклюжую функцию, посчитали предел. У другой функции другой будет.

Но число e почему-то всплывает в целой куче самых разных ситуаций в математике.

Для меня главный смысл числа e раскрывается в поведении другой, куда более интересной функции, y = kx. Эта функция обладает уникальным свойством при k = e, которое можно показать графически так:

В точке 0 функция принимает значение e0 = 1. Если провести касательную в точке x = 0, то она пройдёт к оси абсцисс под углом с тангенсом 1 (в жёлтом треугольнике отношение противолежащего катета 1 к прилежащему 1 равно 1). В точке 1 функция принимает значение e1 = e.

Если провести касательную в точке x = 1, то она пройдёт под углом с тангенсом e (в зелёном треугольнике отношение противолежащего катета e к прилежащему 1 равно e). В точке 2 значение e2 функции снова совпадает с тангенсом угла наклона касательной к ней.

Из-за этого, заодно, сами касательные пересекают ось абсцисс ровно в точках −1, 0, 1, 2 и т. д.

Среди всех функций y = kx (например, 2x, 10x, πx и т. д.), функция ex — единственная обладает такой красотой, что тангенс угла её наклона в каждой её точке совпадает со значением самой функции.

Значит по определению значение этой функции в каждой точке совпадает со значением её производной в этой точке: (ex)´ = ex. Почему-то именно число e = 2,7182818284590…

нужно возводить в разные степени, чтобы получилась такая картинка.

• Именно в этом, на мой вкус, состоит его смысл.
• Числа π и e входят в мою любимую формулу — формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу i и, собственно, числа π и е:
• eiπ + 1 = 0

Почему число 2,7182818284590… в комплексной степени 3,1415926535…i вдруг равно минус единице? Ответ на этот вопрос выходит за рамки заметки и мог бы составить содержание небольшой книги, которая потребует некоторого начального понимания тригонометрии, пределов и рядов.

Меня всегда поражала красота этой формулы. Возможно, в математике есть и более удивительные факты, но для моего уровня (тройка в физико-математическом лицее и пятёрка за комплексный анализ в универе) это самое главное чудо.

Источник: https://ilyabirman.ru/meanwhile/all/pi-and-e

Число е

С замечательным числом e мы впервые встречаемся, начиная изучать показательную функцию, логарифмы и производные. Поэтому для лучшего понимания мы рекомендуем вам прочитать наши статьи «Показательная функция» и «Геометрический смысл производной».

В статье «Показательная функция» мы говорили о важнейшем свойстве функции — при эта функция очень быстро растет. И не просто «быстро растет» — чем больше x, тем больше скорость ее роста, тем круче идет график. Можно сказать, что с увеличением x растут и значения показательной функции, и ее производная. А если аргументом показательной функции является время, то при такая функция является математическим выражением стремительно развивающегося процесса.

Среди показательных функций есть особенная. Называется она экспонента, ее формула . Особенность ее в том, что в каждой точке скорость роста этой функции равна значению самой функции в этой точке. Другими словами, , то есть производная функции равна ей самой.

Логарифм по основанию e называется натуральным и обозначается . Если в уравнении или неравенстве вам встретились такие логарифмы, вы работаете с ними так же, как и с любыми другими, у которых основание больше 1.

Функция также обладает интересным свойством:

Это значит, что с ростом x график логарифмической функции идет более и более полого, скорость роста его уменьшается, что мы и видим.

Формулы для производных функций и содержат в себе выражение :

Число e, как и число , является одной из мировых констант. Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.

Число известно людям с глубокой древности. Оно равно отношению длины окружности к ее диаметру.  А вот с числом e (названным так в честь великого математика Леонарда Эйлера) человечество познакомилось намного позже. Впервые его вычислил математик Якоб Бернулли в начале XVIII века, причем сделал это, решая чисто практическую задачу о начислении процентов на банковский вклад.

В заданиях вариантов ЕГЭ вам встречались задачи, где вклад величиной x помещен в банк под p % годовых. Найти нужно было, например, каким станет вклад через два года.

Рассказывая о решении таких задач, мы вывели удобные формулы:
если величину x увеличить на p процентов, получится
если величину x дважды увеличить на p процентов, получим Именно таким станет вклад через два года;
если вклад пролежит в банке n лет, его величина станет равной

Итак, если вклад поместить банк под 10% годовых, он вырастет за год в 1,1 раз, за два года — в 1,21 раза, за десять — примерно в 2,6 раза. Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты.

Давайте так и сформулируем задачу. Пусть банк начисляет каждый день по одной сотой процента.

Во сколько раз вырастет вклад через 10000 дней (это двадцать семь с лишним лет)? Иными словами, чему приближенно равна величина
? И к чему будет стремиться величина , если n стремится к бесконечности?
Вот такую задачу и решал Бернулли.

Если n будет очень большим, или, как говорят математики, бесконечно большим, будет стремиться к бесконечности (то есть больше миллиона, больше миллиарда, больше двух миллиардов. . . ) — то величина  будет, наоборот, очень малой. Можно сказать, что будет стремиться к нулю.

Оказывается, что в этом случае величина  будет стремиться к числу e. Если банк каждый год начисляет по 1%, через 100 лет вклад увеличится примерно в e раз (напомним, что e ≈ 2,718).

Еще большая точность будет достигнута, если каждый день банк начисляет по 0,01 процента. Через 10000 дней вклад увеличится примерно в e раз.

 Итак, если n стремится к бесконечности, то величина стремится к числу e.

Этот неожиданный факт называется вторым замечательным пределом. Вы встретитесь с ним в курсе математического анализа.

Источник: https://ege-study.ru/ru/ege/materialy/matematika/chislo-e/

Число е в реальной жизни

Содержание

стр.
Общая характеристика работы ………………………………………	2
Основное содержание работы…………………………………………	4
Экспериментальная часть работы……………………………………	10
Заключение………………………………………………………………	11
Список использованной литературы………………………………..	12

•                            Число е  в реальной жизни.
• Общая характеристика работы
• «…Ею порождено многое из того,Что достойно упоминания»
•  «Ода экспоненте»
• английский поэт  Элмер  Брил  .

Актуальность Возникновение чисел в нашей жизни не случайность. Невозможно представить себе общение без использования чисел. История чисел увлекательна и загадочна.

Человечеству удалось установить целый ряд законов и закономерностей мира чисел, разгадать кое-какие тайны и использовать свои открытия в повседневной жизни.

Без замечательной науки о числах – математики – немыслимо сегодня ни прошлое, ни будущее. А сколько ещё не разгаданного!

1. Цель   константа  е — это фундаментальная константа, которая отражается в темпах роста .
2. Объект исследования:  найти    невидимую  связь между математикой и жизнью!  
3. Предмет исследования:  Фундаментальный характер  числа е      появляется при изучении роста какой-нибудь величины.
4. Гипотеза  в окружающей нас действительности всё  построено по удивительно гармоничным законам с математической точностью.
5. Цель и гипотеза исследования определили его задачи:

• Раскрыть понятия «число Эйлера», «экспонента», «экспоненциальность мира» и научиться «видеть» их в повседневной жизни .
• Познакомиться с определением числа е.
• Рассмотреть фундаментальный характер  числа е    при изучении роста какой-нибудь величины.  

 Методами исследовательской работы стали:

• Теоретические (анализ, синтез, сравнение научной и учебной литературы, а также ресурсов сети Интернет)
• Эмпирический (наблюдение, опрос учащихся и учителей МБОУ «Большекайбицкая СОШ»)
• Качественный анализ полученных в ходе исследования результатов.

• Исследование проводилось на базе МБОУ «Большекайбицкая средняя общеобразовательная школа» Кайбицкого муниципального района Республики Татарстан среди 40 учащихся 11-ых классов и 15 учителей.
• Этапы исследования:
• I этап. Изучение теоретических аспектов «числа е», а также истории возникновения знаменитого числа;

II этап. Разработка вопросов для опросника, проведение опроса с учащимися и учителями. Анализ результатов опроса, выявление первичных результатов;

III этап. Практическая работа – сделать буклет по данной теме и выступить перед одноклассниками , подвести итоги  исследовательской работы.

Основное содержание работы

 В незапамятные времена, научившись считать, люди познали меру количества – число. Вглядываясь в сочетания чисел, они с изумлением увидели, что числа имеют какую-то самостоятельную жизнь, удивительную и полную тайны; тайны необъяснимой и поэтому загадочной и многозначительной… Священные, волшебные, загадочные, таинственные, совершенные.

…       Как только их не называли! «Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетарными, а другими – магическими», — писал о них известный французский математик, один из создателей теории чисел Пьер де Ферма.

Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множества тайн.…

В своей жизни каждый из нас стакивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них.

Разговор об экспоненциальности нашего мира невозможно начать иначе, как с рассказа о так называемом «числе е».

Число е – это основание натуральных логарифмов и важнейшая математическая константа (обозначается строчной латинской буквой «e»), которая в высшей математике встречается буквально на каждом шагу, она играет особенно важную роль в дифференциальном и интегральном исчислении. Иногда число e называют числом Эйлера. Леонард Эйлер (1707 – 1783 гг.

) – это самый плодовитый в мире (на открытия) гениальный математик. Именно Эйлер первым ввел символ е (с этой буквы начинается его фамилия – Euler) и сделал так много открытий, связанных с числом е, что, в конце концов, е стали называть числом Эйлера. Численное значение указанного числа следующее:

e = 2,7 1828 1828 459045235360287471352662497757…,

Число е – трансцендентное число (доказал Ш. Эрмит в 1873 г.

), то есть оно не является корнем никакого многочлена с целыми коэффициентами, и не существует закона, по которому чередуются цифры после запятой в значении числа е (ещё в 1961 г.

с помощью ЭВМ было получено 100265 десятичных знаков). Предполагается, что e – это нормальное число, то есть вероятность появления разных цифр в его (бесконечной!) записи одинакова.

Иногда число е малообоснованно называют неперовым числом, по имени изобретателя логарифмов Джона Непера (1550–1617). 

Число e может быть определено несколькими способами.

• Число е обозначает предел, к которому стремится выражение е* = (1 + 1/N)^N, когда целочисленный параметр N устремляется к бесконечности: N = 1, 2, 3, 4, 5, 6, 7,… [символ ^ («крышка») будет означать «возведение в степень», то есть выражение в круглой скобке (1+1/N) возводится в степень N]. Короче говоря, выражение е* устремляется к числу е = 2,718281828459045… .

x	y
1	(1 + 1 / 1)1	= 2
2	(1 + 1 / 2)2	= 2,25
3	(1 + 1 / 3)3	= 2,3703703702…
10	(1 + 1 / 10)10	= 2,5937424601…
100	(1 + 1 / 100)100	= 2,7048138294…
1000	(1 + 1 / 1000)1000	= 2,7169239322…
∞	lim× → ∞	= 2,7182818284590…

• Число е  – это сумма бесконечного ряда: е = 1/0! + 1/1! +1/2! +1/3! +1/4! + 1/5! + … (в знаменателе стоят натуральные числа 0, 1, 2, 3, 4, 5, 6, 7, …, идущие до бесконечности).
• Число е – это единственное число, для которого выполняется следующее условие: площадь области под графиком y = 1/x на интервале от  х = 1 до x = e равна 1.

Число е можно представить в виде бесконечной цепной дроби (её открыл Эйлер):

е = 2 + 1/(1 +1/(2+2/(3+3/(4+4/…)))).

 Как и число π, е- трансцендентное число, то есть оно не может быть корнем какого-нибудь алгебраического уравнения с рациональными коэффициентами. Подобно тому,  как с помощью циркуля и линейки невозможно построить отрезок прямой, длина которого в соответствующих единицах в точности равна π, не существует и способа построения отрезка, длина которого выражалась бы числом е.  

Имея огромное применения в математике, остается неотмеченным вопрос: как же его используют в реальной жизни, то есть каково практическое применение числа Эйлера.

Число е встречается  буквально на каждом шагу в высшей математике, в особенности в задачах теории вероятностей, в реальной жизни оно проявляет себя ярче всего при росте какой – либо величины, будь то рост клетки или банковского счета.

  Предположим, что кто-то положил один доллар в банк, выплачивающий 4% годовых.  Если проценты простые, то каждый год сумма вклада возрастет на 4% от первоначального капитала. Каждый доллар через двадцать пять лет «вырастет» и превратится в два доллара.

Если же банк выплачивает сложный процент, то доллар будет расти быстрее, потому что после каждого начисления процентов капитал немного увеличивается и в следующий раз процент начисляется от большой суммы.

Чем чаще производят перерасчет и прибавление прибыли к основному капиталу, тем быстрее растет вклад. При ежегодном начислении сложных процентов доллар за 25 лет превратится в (1+1/25)25 , то есть в 2,66 долларов.

При начислении сложных процентов каждые полгода [если банк выплачивает 4 (сложных) процента годовых, то прирост  вклада за каждые шесть месяцев составляет 2%]  доллар за 25 лет превратится в (1+1/50)50 , или 2,69 доллара.

В действительности ничего подобного не произойдет. Через 25 лет один доллар вырос бы до величины (1+1/n)n  , где n- число начисленной прибыли. При n, стремящемся  к бесконечности, это выражение стремится к пределу, равному 2,718  , что всего на 3 цента больше той суммы, которая получилась бы, если бы прибыль начислялась лишь раз в полгода.

Этот предел и называется числом е. 

Предположим, что в банке, выплачивающем простой процент, один доллар через какой-то промежуток времени удваивается. При непрерывном начислении  прибыли доллар за то же время превратился бы в е долларов независимо от того, сколько простых процентов прибыли выплачивает в действительности банк.

Однако за очень большой промежуток времени даже очень маленькая ежегодная прибыль может увеличить первоначальный капитал до гигантской суммы.

Если бы в первом году нашей эры кто-то положил один доллар в банк, выплачивающий 4% годовых, то к 2015 году на его счету было бы уже (1,04)2015  долларов, то есть сумма вклада выражалась бы огромным числом!

       Не все величины возрастают так, как растет капитал в рассмотренных нами примерах. Тип роста, о котором шла речь, обладает одной весьма важной особенностью:  в каждый момент времени скорость роста пропорциональна величине того, что возрастет. Иначе говоря, отношение приращения изменяющейся величины к ее текущему значению всегда одно и то же.

Величины такого типа изменяются подобно снежному кому, несущемуся с вершины горы: чем больше становится ком, тем быстрее налипает на него снег. Этот тип роста свойствен многим процессам в живой и неживой природе. Все они описываются формулами, в которые входит функция y=е х.

Эта функция настолько важна, что она в отличие от других показательных функций, у=а х, где а ≠е (например, у=2х ), получила особое название. Её называют экспоненциальной функцией или кратко экспонентой. Экспонента с точностью совпадает со своей производной. Именно этим и объясняется причина столь частого появления экспоненты в формулах математического анализа.

Источник: https://nsportal.ru/ap/library/drugoe/2016/12/04/chislo-e-v-realnoy-zhizni-0