Стандартное обозначение площади — S
Площадь

Пусть длина стороны квадрата равна a, тогда формул квадрата:
S = a ⋅ a = a2

Пусть длины сторон прямоугольника равны a и b
S = a ⋅ b

Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
S = a ⋅ ha = b ⋅ hb

Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude).
Тогда формула площади:
$S = frac{(a + b)cdot h}{2}$

$P = picdot r^2$
$pi=3,14$
Площадь прямоугольного треугольника

$S=frac{a cdot b}{2}$
$S=frac{c cdot h_c}{2}$
Площадь треугольника — калькулятор
Стороны треугольника:
ABC — треугольник

длина его сторон: a, b, c и длина его высот: ha, hb и hc.
S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)
S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)
- p = ½(a + b + c)
- S = √p(p — a)(p — b)(p — c) — формула Герона
- $S = R^2sin(A) cdot sin(B) cdot sin(C) = frac{abc}{4R}$
где R — радиус описанной окружности 
- $S = ABcdot DE = BC cdot DF$
$S = AB cdot AD sin alpha$ - $S = frac12 AC cdot BD sin gamma$
Площадь выпуклого четырехугольника

$S = frac12 AC cdot BD sin varphi $
Площадь правильного многоугольника

$S = frac14 ncdot a^2cdot ext{ctg}(frac{pi}{n})$
n — число ребер(вершин).
$pi=3,14159265359$
Источник: https://www.math10.com/ru/geometria/ploshad.html
Как найти площадь геометрических фигур?
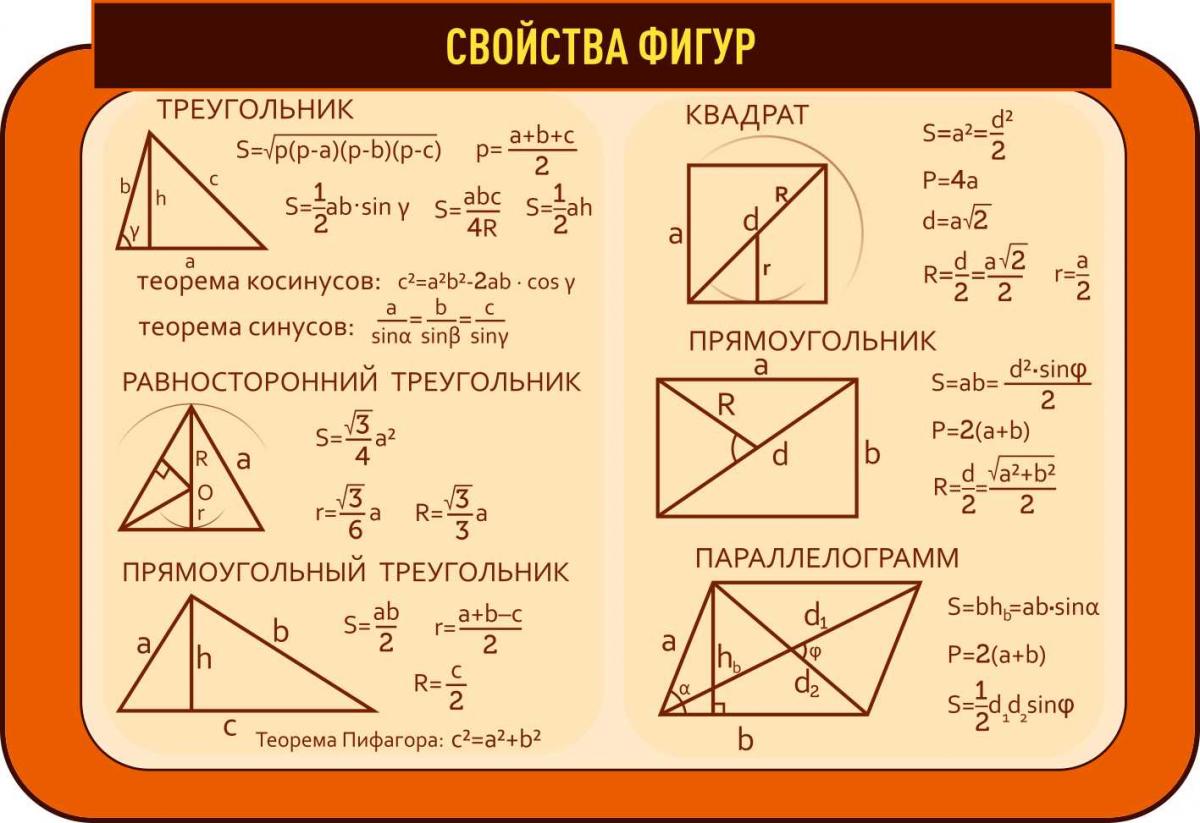
Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Треугольник
Прямоугольник
Квадрат
Параллелограмм
Ромб
Трапеция
Круг
Как найти площадь треугольника?
1. Самая известная формула площади треугольника по стороне и высоте:
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.

Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. 
Если треугольник тупоугольный, то высота опускается на продолжение основания:

Если треугольник прямоугольный, то основанием и высотой являются его катеты:

2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.


- Главное условие – угол берется между двумя известными сторонами.
- 3. Формула площади по трем сторонам (формула Герона):
S = ![]()
где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.

4. Формула площади треугольника через радиус описанной окружности:
S =
где a, b и с – стороны треугольника, а R – радиус описанной окружности.

5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.
Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
2. Также площадь квадрата можно найти через его диагональ:
S = d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
- Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
- 2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα
3. Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
1. Площадь круга можно найти через радиус:
S = π r2
2. Площадь круга можно найти через диаметр:
S = πd2/4
Источник: https://boeffblog.ru/matematika/matematika-osnovy/kak-najti-ploshhad-geometricheskix-figur
Площади четырехугольников
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
- В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
- S = ab,
- которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | a и b – смежные стороны |
 |
d – диагональ,φ – любой из четырёх углов между диагоналями | ||
 |
S = 2R2 sin φПолучается из верхней формулы подстановкой d=2R | R – радиус описанной окружности,φ – любой из четырёх углов между диагоналями | |
| Параллелограмм |  |
S = a haПосмотреть вывод формулы | a – сторона,ha – высота, опущенная на эту сторону |
 |
S = absin φПосмотреть вывод формулы | a и b – смежные стороны,φ – угол между ними | |
 |
d1, d2 – диагонали,φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
| Посмотреть вывод формулы | d – диагональ квадрата | ||
| S = 2R2Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a haПосмотреть вывод формулы | a – сторона,ha – высота, опущенная на эту сторону | |
| S = a2 sin φПосмотреть вывод формулы | a – сторона,φ – любой из четырёх углов ромба | ||
| Посмотреть вывод формулы | d1, d2 – диагонали | ||
| S = 2arПосмотреть вывод формулы | a – сторона,r – радиус вписанной окружности | ||
| Посмотреть вывод формулы | r – радиус вписанной окружности,φ – любой из четырёх углов ромба | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания,h – высота | |
| S = m h | m – средняя линия,h – высота | ||
| Посмотреть вывод формулы | d1, d2 – диагонали,φ – любой из четырёх углов между ними | ||
| Посмотреть вывод формулы | a и b – основания,c и d – боковые стороны | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны,φ – угол между ними | |
| a и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b. | |||
| S = (a + b) rПосмотреть вывод формулы | a и b – неравные стороны,r – радиус вписанной окружности | ||
| Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали,φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | ,Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника,p – полупериметр,Формулу называют «Формула Брахмагупты» |
| Прямоугольник |
| S = abгдеa и b – смежные стороны |
|
|
| Параллелограмм |
|
|
|
| Квадрат |
| S = a2гдеa – сторона квадрата |
| S = 4r2гдеr – радиус вписанной окружности |
|
|
| Ромб |
|
|
|
|
|
| Трапеция |
|
| S = m hгдеm – средняя линия,h – высота |
|
|
| Дельтоид |
| S = ab sin φгдеa и b – неравные стороны,φ – угол между ними |
| гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b. |
|
|
| Произвольный выпуклый четырёхугольник |
|
| Вписанный четырёхугольник |
|
| Прямоугольник |
| S = abгдеa и b – смежные стороны |
|
|
| Параллелограмм |
|
|
|
| Квадрат |
| S = a2гдеa – сторона квадрата |
| S = 4r2гдеr – радиус вписанной окружности |
|
|
| Ромб |
|
|
|
|
|
| Трапеция |
|
| S = m hгдеm – средняя линия,h – высота |
|
|
| Дельтоид |
| S = ab sin φгдеa и b – неравные стороны,φ – угол между ними |
| гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b. |
|
|
| Произвольный выпуклый четырёхугольник |
|
| Вписанный четырёхугольник |
|
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
- Рис. 1
- Доказательство. В соответствии с рисунком 1 справедливо равенство:
- что и требовалось доказать.
- Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
- S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
- SABCD = SAEFD = a ha ,
- что и требовалось доказать.
- Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
- S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
- Рис. 3
- Доказательство. Поскольку
- ha = b sin φ,
- то, в силу утверждения 2, справедлива формула
- S = a ha = ab sin φ,
- что и требовалось доказать.
- Утверждение 4. Площадь ромбаромба можно найти по формуле
- ,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
- что и требовалось доказать.
- Утверждение 5. Площадь трапеции можно найти по формуле
- ,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,
где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,
- что и требовалось доказать.
- Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
- S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7).
Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник: https://www.resolventa.ru/spr/planimetry/sqf.htm
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота (BE), проведённая между длинными сторонами, короче высоты (BF), проведённой между короткими сторонами.

Так как стороны ромба одинаковы, то высоты ромба также одинаковы: (BE = BF).
 Площадь произвольного параллелограмма
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.

- Проведём высоты из двух вершин (B) и (C) к стороне (AD) .
- Прямоугольные треугольники (ABE) и (DCF) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
- Параллелограмм (ABCD) и прямоугольник (EBCF) — равновеликие, так как состоят из равных фигур:
- SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
- Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
- SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
- Если обозначить сторону через (a), высоту — через (h), то:
- Sп−гр=a⋅h.
- Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.

- SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
- Формула определения площади ромба:
- Sромба=d1⋅d22.
- Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
- Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
- Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.

- Sтреуг=aha2, где (h) — высота (на рисунке — (BE)), проведённая к стороне (a) (на рисунке — (AD)).
- Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
- Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
- — формула Герона, где (a), (b) и (c) — стороны треугольника, (p) — полупериметр треугольника.
Площадь прямоугольного треугольника
- Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
- S=a⋅b2, где (a) и (b) — катеты.
- Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами (17) см, (39) см, (44) см.
- Решение:
- p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
- Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.
Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны (15) см, (13) см, (4) см.
- Решение:
- используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
- Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому (a =) (15) см.
- SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
- Составляем уравнение:
- 15⋅h2=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами (17) см и (39) см, длина диагонали равна (44) см. Вычислим площадь параллелограмма.
- Решение:
- диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
- Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.

Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.

- SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
- Если обозначить параллельные стороны (основания) трапеции через (a) и (b), высоту через (h), то:
- Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Источник: https://www.yaklass.ru/p/geometria/8-klass/ploshchadi-figur-9235/ploshchad-parallelogramma-treugolnika-i-trapetcii-9238/re-5498cfac-2fcc-49e0-a4ac-23cf5dabe20d
Площадь фигур
Определение площади Формулы площадей фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
 SEKFM = EK · EK
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
S = a2
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
 SABCD = AB · BC
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
 SABCE = AB · BC SEFKL = 10 · 3 = 30 м2 SCDEF = FC · CD SCDEF = 7 · 5 = 35 м2
SABCE = AB · BC SEFKL = 10 · 3 = 30 м2 SCDEF = FC · CD SCDEF = 7 · 5 = 35 м2
- Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников. S = SABCE + SEFKL S = 30 + 35 = 65 м2
- Ответ: S = 65 м2 — площадь огородного участка.
- Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC SABCD = 5 · 4 = 20 см2
- S ABC = SABCD : 2
- S ABC = 20 : 2 = 10 см2
- S ABC = S ACD = 10 см2
Источник: http://math-prosto.ru/?page=pages/area/area_figures.php
Формулы для нахождения площадей

- На завтрак были круглая яичница, параллелепипедная булочка
и кофе в цилиндрической кружке. - Геометрия мне очень даже пригодилась в жизни, да.
В стать «Есть ли у треугольника площадь» мы рассмотрели основные формулы для нахождения площади простейших геометрических фигур. Для решения большинства задач по нахождению площади плоских фигур эти формул вполне достаточно.
Их обычно используют при решении типовых задач на контрольных или при сдаче ЕГЭ. Но вы должны понимать, это далеко не полный список формул для нахождения площади геометрических фигур. Более того, это лишь вершина айсберга.
Взгляните что там, в глубине.
Формулы площади квадрата
Всем хорошо известны формулы для нахождения площади квадрата с известной стороной или диагональю. Но как быть, если эти величины нам неизвестны? Все очень просто! Нам помогут формулы для нахождения площади квадрата через:
- радиус вписанной окружности
-

- радиус описанной окружности
линию выходящую из угла на
середину стороны квадрата
через периметр
Формулы площади прямоугольника
Для прямоугольника помимо общеизвестной формулы нахождения площади перемножением длин двух его сторон существуют формулы для нахождения площади через:
известные диагонали и угол между ними
известную длину стороны и угол между этой стороной и диагональю
известный периметр и длину одной стороны
Формулы площади треугольника
- Все хорошо знают три основные формулы нахождения площади треугольника. Добавлю еще парочку:
- по трем сторонам и радиусу вписанной окружности
- здесь p=(a+b+c) — полупериметр
- по трем сторонам и радиусу описанной окружности
Формулы площади параллелограмма
- Для нахождения площади параллелограмма также существует несколько дополнительных формул:
- по известным диагоналям и углу между ними
- по двум известным высотам и углу между ними
Как вы могли заметить, некоторые формулы для нахождения площадей очень похоже. Строго говоря, квадрат, ромб, прямоугольник, трапеция и параллелепипед являются частными случаями другой геометрической фигуры — выпуклого четырехугольника. Поэтому, зная формулы для нахождения площади четырехугольника, всегда можно найти площадь любой другой фигуры.
Формулы площади четырехугольника
- формула площади выпуклого четырехугольника по известным длинам диагоналей и углу между ними
- формула площади выпуклого четырехугольника по длине периметра и радиусу вписанной окружности
- здесь p= (a+b+c+d)/2 — полупериметр
- формула площади выпуклого четырехугольника по известным длинам сторон и значениям противоположных углов
- здесь p=(a+b+c+d)/2 — полупериметр
- Θ=(f1+f2)/2 — полусумма углов
- формула площади выпуклого четырехугольника вокруг которого можно описать окружность
- здесь p=(a+b+c+d)/2 — полупериметр
Теперь вы знаете достаточно формул для нахождения площадей плоских фигур. Этого вполне достаточно для того спокойно чувствовать себя на экзамене и чтобы спокойно решать простейшие задачки по ЕГЭ. Но не надо думать, что способы нахождения площади ограничиваются этими формулами. Ведь помимо уже известных вам треугольников и квадратов существует огромное множество самых разнообразных геометрических фигур, таких как вогнутые четырехугольники, выпуклые и вогнутые многоугольники, а также фигуры , вообще не имеющие какой-либо определенной формы. Кроме того, существуют способы нахождение площади по формулам аналитической геометрии (когда известны координаты вершин или вектора сторон), или с помощью интегрального исчисления.
Ну а в заключение хочу вам представить еще одну универсальную формулу − формулу для нахождения площади эллипса: площадь эллипса равна произведению длин большой и малой полуосей эллипса на число ∏
Источник: http://df-dt.com/formuly-ploshhadej.html
Учим формулы легко и просто: площади плоских фигур — площадь треугольника и многоугольника
Продолжаем учить формулы легко и быстро
Для начала вспомним
Площадь треугольника
Конечно, вычислить площадь прямоугольника достаточно легко. Но далеко не все фигуры мы можем представить в виде нескольких прямоугольников. Чаще всего фигуры легко разделить на треугольники.
ABCDE — выпуклый многоугольник, который можно разбить на треугольники: EAB, BEC и ЕСD
Если сложить площади таких треугольников, то можно будет узнать и площадь многоугольника. Формулы площади треугольника позволят решить целый ряд геометрических задач, причем, разными способами, ведь площадь треугольника можно выразить через его различные элементы.
Итак, формул площади треугольника несколько, но каждая из них важна. Если вам сложно запомнить комбинацию букв — учите правило.
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения двух его сторон, умноженной на синус угла между ними
Источник: https://zen.yandex.ru/media/id/59ac54054bf161a5f926a729/5a38dc114826779f2a1d9e6c
Вычисление объемов фигур
Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.
Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.
Базовая информация
Объем геометрической фигуры — это количественная характеристика пространства, которое занимает тело. Она определяется его формой и размерами. Чтобы задачи на вычисление объемов геометрических фигур не вызывали затруднений, рекомендуем освежить в памяти основные формулы.
- Объем куба равняется кубу длины его грани.
- Объем призмы равняется произведению площади основания фигуры на высоту. Чтобы его рассчитать, воспользуйтесь следующий формулой: V = So h, где V — объем призмы, So — площадь ее основания, h — ее высота.
- Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты. Формула для его расчета: V = a · b · h, где a — длина, b — ширина, h — высота.
- Объем пирамиды равняется трети от произведения площади ее основания на высоту.
- Объем цилиндра равняется произведению площади его основания на высоту. Формулы для его расчета:
Для его расчета используется формула: V = a3, где V — объем куба, a — длина его грани.
Рассчитать его можно по формуле: V = 1/3 So· h , где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.
V = π R2 h V = So h
Где V — объем цилиндра, So — площадь основания цилиндра, R — радиус цилиндра, h — высота цилиндра, π = 3.141592.
Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?
Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.
Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.
Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.
Источник: https://shkolkovo.net/catalog/geometriya_v_prostranstve_stereometriya/ploshhad_i_obem_figur




