Графики тригонометрических функций.
Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах.
Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
 График функции y=sinA (синусоида) График функции y=sinA (синусоида) |
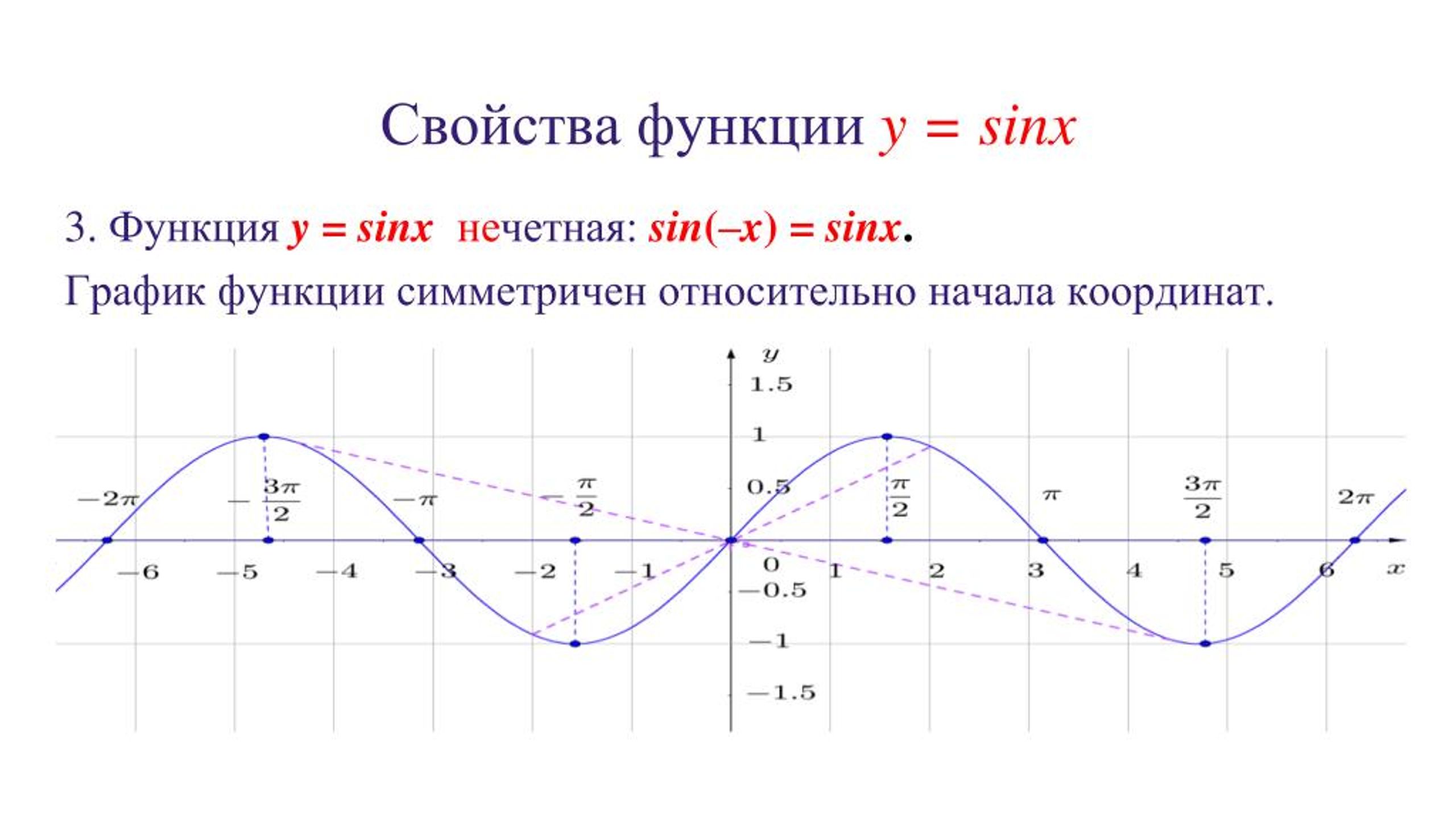 График функции y=cosA (косинусоида) График функции y=cosA (косинусоида) |
 График функции y=tgA (тангенсоида) График функции y=tgA (тангенсоида) |
Из графиков видно что:
- Графики синуса и косинуса колеблются в пределах между -1 и 1
- Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90o
- Кривые синуса и косинуса непрерывны и повторяются с периодом 360o , кривая тангенса имеет разрывы и повторяется с периодом 180o .
Углы произвольной величины

График. Положительное или отрицательное направление при движении по окружности.
 Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.) Пусть ОА вращается дальше таким образом, что Θ2 — любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.) Пусть ОА вращается дальше таким образом, что Θ2 — любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
График. Поcтроение углов в различных квадрантах.
 Пусть ОА вращается дальше таким образом, что Θ4- любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -.
Пусть ОА вращается дальше таким образом, что Θ4- любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -.
В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева.
График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
 Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o — 19,03o = 160,97o . Таким образом, 19,03o и 160,97o — это углы в диапазоне от 0o до 360o , синус которых равен 0,3261.
Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o — 19,03o = 160,97o . Таким образом, 19,03o и 160,97o — это углы в диапазоне от 0o до 360o , синус которых равен 0,3261.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. График. Нахождение всех углов по заданному значению синуса (пример)
Пример 1
Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 
Решение: Углы, синус которых равен -0,7071o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).
График. Нахождение всех углов по заданному значению синуса (пример)
Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o — 45 o = 315o .
 Примечание. Калькулятор дает только один ответ. График. Нахождение всех углов по заданному значению синуса (пример)
Примечание. Калькулятор дает только один ответ. График. Нахождение всех углов по заданному значению синуса (пример)
- Пример 2
- Найти все углы между 0o и 360o , тангенс которых равен 1, 327.

- Решение:
- График. Нахождение всех углов по заданному значению тангенса (пример)
Тангенс положителен в первом и третьем квадрантах — рис. слева.
Из рис ниже Θ = arctg1,327= 53o . Два угла в диапазоне от 0o до 360o , тангенс которых равен 1,327, это 53o и 180o + 53 o, т.е. 233o . График. Нахождение всех углов по заданному значению тангенса (пример)
Построение синусоиды и косинусоиды
Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая — это ТS, а горизонтальная — ОS.
График. Построение синусоиды.
Из определения тригонометрических функций
sin30o=TS/TO=TS/1, т.е. TS= sin30o и cos30o=OS/TO=OS/1, т.e. OS=cos30o
Вертикальную составляющую TS можно перенести на график в виде T'S', что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90o.
График. Построение косинусоиды.
Синусоидальные и косинусоидальные графики
| График. y=sinA и y=sin2A (синусоиды). | График. y=sinA и y=sin(1/2)A (синусоиды). |
| График. y=cosA и y=cos2A (косинусоиды). | График. y=cosA и y=cos(1/2)A (косинусоиды). |
Периодические функции и период Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями. Функции y=sinA и y=cosA повторяются через каждые 360o (или 2π радиан), поэтому 360o называется периодом этих функций.
Функции y=sin2A и y=cos2A повторяются через каждые 180o (или π радиан),поэтому 180o — это период для данных функций. В общем случае если y=sinpA и y=cospA (где р — константа), то период функции равен 360o/p (или 2π/p радиан ).
Следовательно, если y=sin3A, то период этой функции равен 360o/3= 120o, если y=cos4A, то период этой функции равен 360o/4= 90o.
Амплитуда Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для y=5cos2A амплитуда равна 5, а период — 360o/2= 180o.
Пример 3.
Построить y=3sin2A в диапазоне от А= 0o до А=360o.
Решение:
Амплитуда =3, период = 360o/2 =180o. График. Построение y=3sin2A (синусоида).
Пример 4.
Построить график y=4cos2x в диапазоне от х=0o до х=360o
Решение:
Амплитуда = 4. период = 360o/2 =180o.
График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения Кривые синуса и косинуса не всегда начинаются в 0o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α — сдвиг фазы относительно y=sinA и y=cosA.
Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o.
График. y=sin(A-60o) (синусоида).
Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже.
Если кривая y=cosA начинается в 0o, то кривая y=cos(A+45o) начинается на 45o левее (т.е. ее нулевая величина находится на 45o раньше ). Таким образом, говорят, что график y=cos(A+45o) опережает график y=cosA на 45o. График. y=cos(A+45o) (косинусоида). В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90o левее, т.е. опережает ее на 90o. Следовательно, cosA=sin(A+90o).
Пример 5.
Построить график y=5sin(A+30o) в диапазоне от А=0o до А=360o
Решение: Амплитуда = 5, период = 360o/1 = 360o. 5sin(A+30o) опережает 5sinA на 30o т.е. начинается на 30o раньше. График y=5sin(A+30o) (синусоида).
Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0o до А=360o.
Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).
Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt. Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда Т=2π/ ω (с), где
Т — это период
Число полных периодов, проходящих за 1 секунду, называется частотой f. Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц Следовательно, угловая скорость
- ω=2πf рад/с.
- Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то А — амплитуда ω — угловая скорость 2π/ ω — период Т, с ω/2π — частота f, Гц
- α — угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.
Пример 7. Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)
Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно, период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс частота f = 1/Т = 1/0,022 = 45,46 Гц фазовый угол α = 0,26 рад. = (0,26*180/π)o = 14,9o.
- Пример 8.
- Решение
- Следовательно, смещение 3sin(110πt + α) м.
- Следовательно α=arcsin0,33=19o
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α). Амплитуда = максимальное смещение = 3м Угловая скорость ω=2πf = 2π(55) = 110 πрад./с При t=0 смещение = 100см=1м. Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33 Итак, смещение равно 3sin(110 πt + 0,33).
Пример 9. Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти: а) Амплитуду, период, частоту и фазовый угол (в градусах) б) значение напряжения при t =0 в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение: а) Амплитуда равна 350 В, угловая скорость равна ω=40π Следовательно, период Т=2π/ ω=2π/40π=0,05 с =50мс частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31oс запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31o)=-180,25 В в) Если t =10 мс, то v=350sin(40π10/103-0,542)=350sin(0,714)=350sin41o =229,6 В г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
График. Колебательный механизм (пример, синусоида).
v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад. 40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс
Источник: https://dpva.ru/Guide/GuideMathematics/DiagramsConstruction/TrigonometricCurves/TrigonometricCurvesPrint/
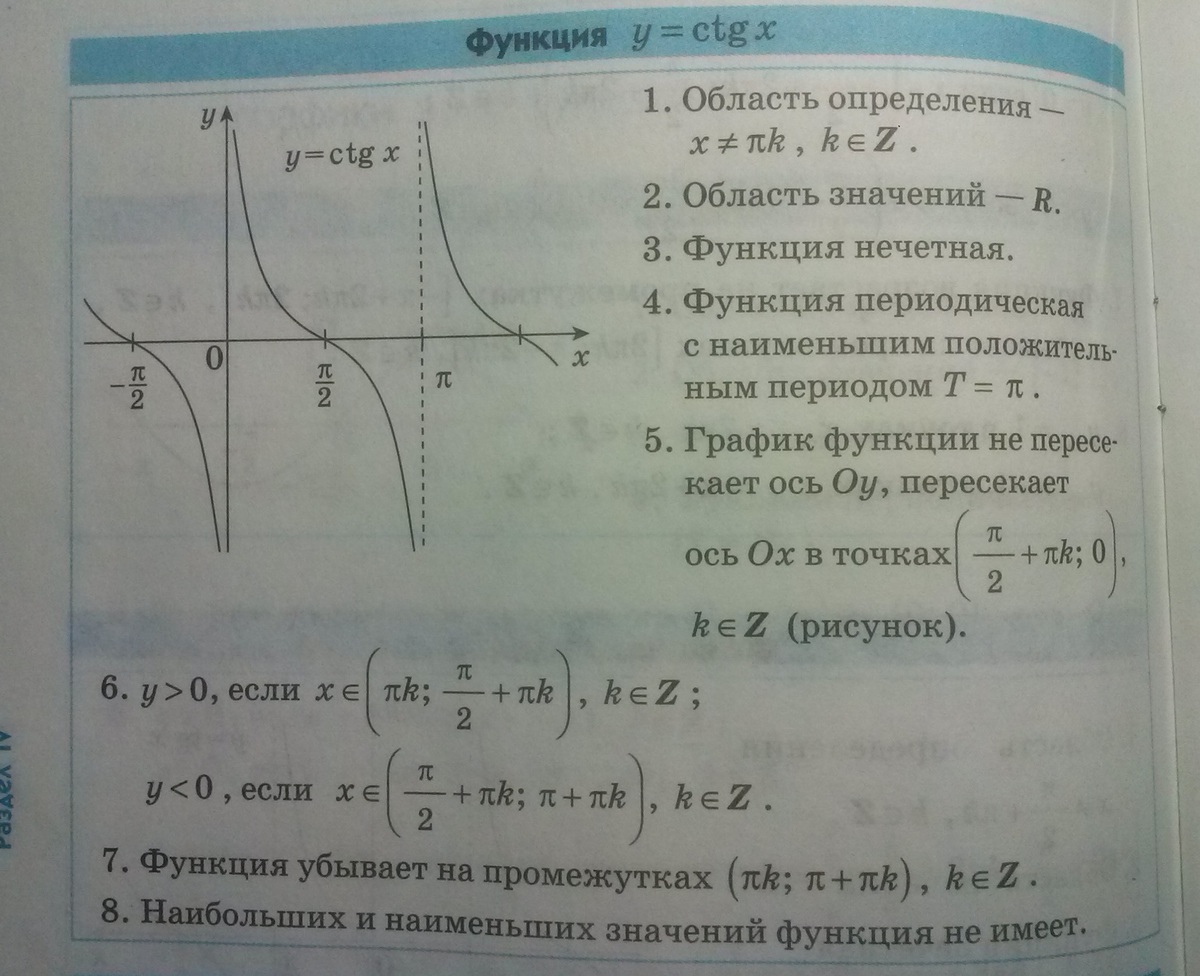
График функции y=tg x
Как построить график функции y=tg x? Для начала рассмотрим график тангенса на интервале (-π/2;π/2).
Число π округлим до целого:
![]()
Единичный отрезок берём длиной в 2 клеточки тетради. В этом случае числу π соответствует отрезок длиной в 6 клеточек, числу π/2 — 3 клеточки, π/6 — 1 клеточка, π/4 — 1,5 клеточки, π/3 — 2 клеточки.
- В область определения функции y=tg x не входят числа
-
- Прямые
-

для графика тангенса являются вертикальными асимптотами, то есть график к ним стремиться, но никогда не достигнет. Асимптоты принято изображать пунктирными линиями.
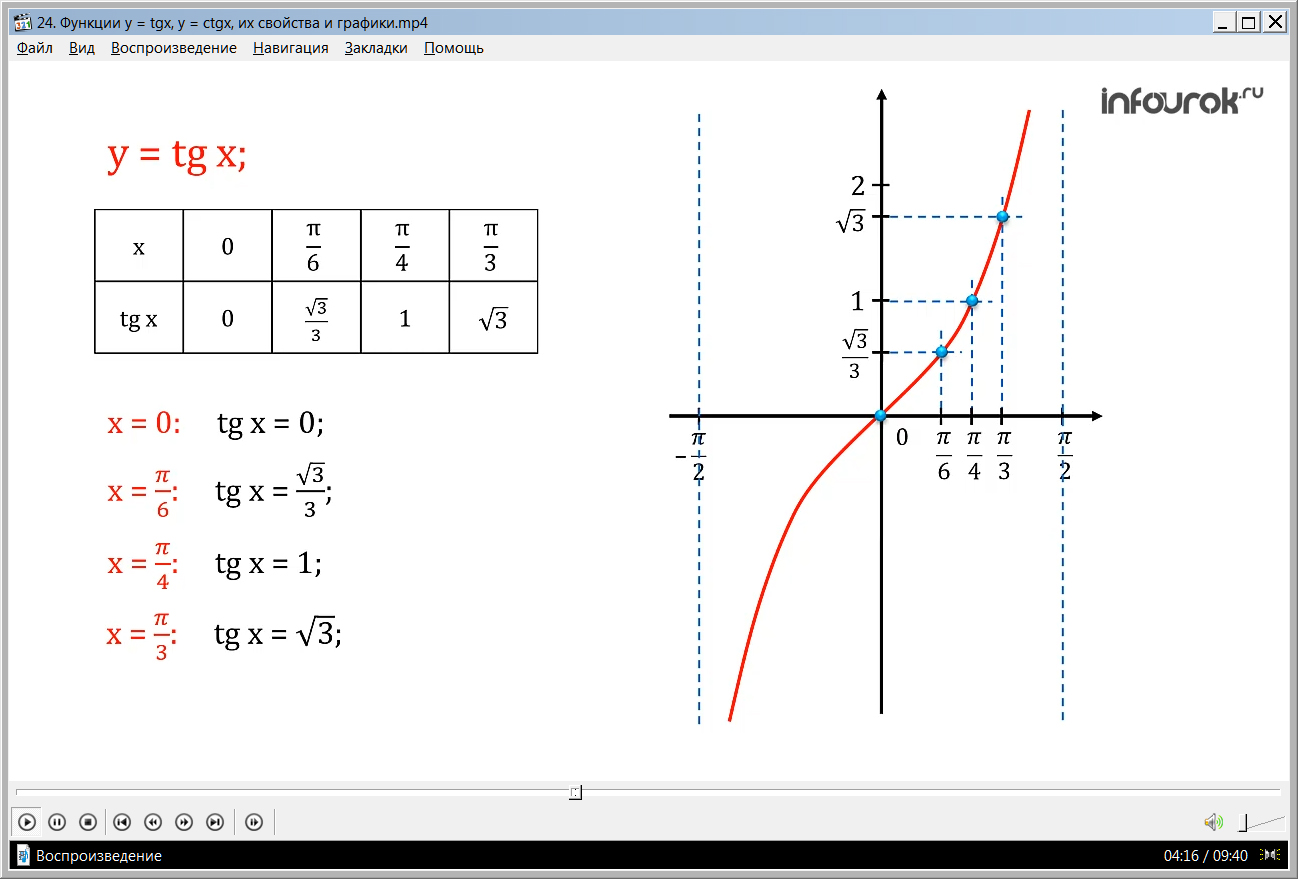
- Составим таблицу значений тангенса на промежутке [0;π/2):
-

- На координатной плоскости отмечаем полученные точки и асимптоты.
- Так как y=tg x — нечётная функция, её график симметричен относительно начала координат:

Поскольку функция tg x — периодическая с периодом T=π, график тангенса, взятый на интервале (-π/2;π/2), повторяется влево и вправо, на плюс и на минус бесконечность:
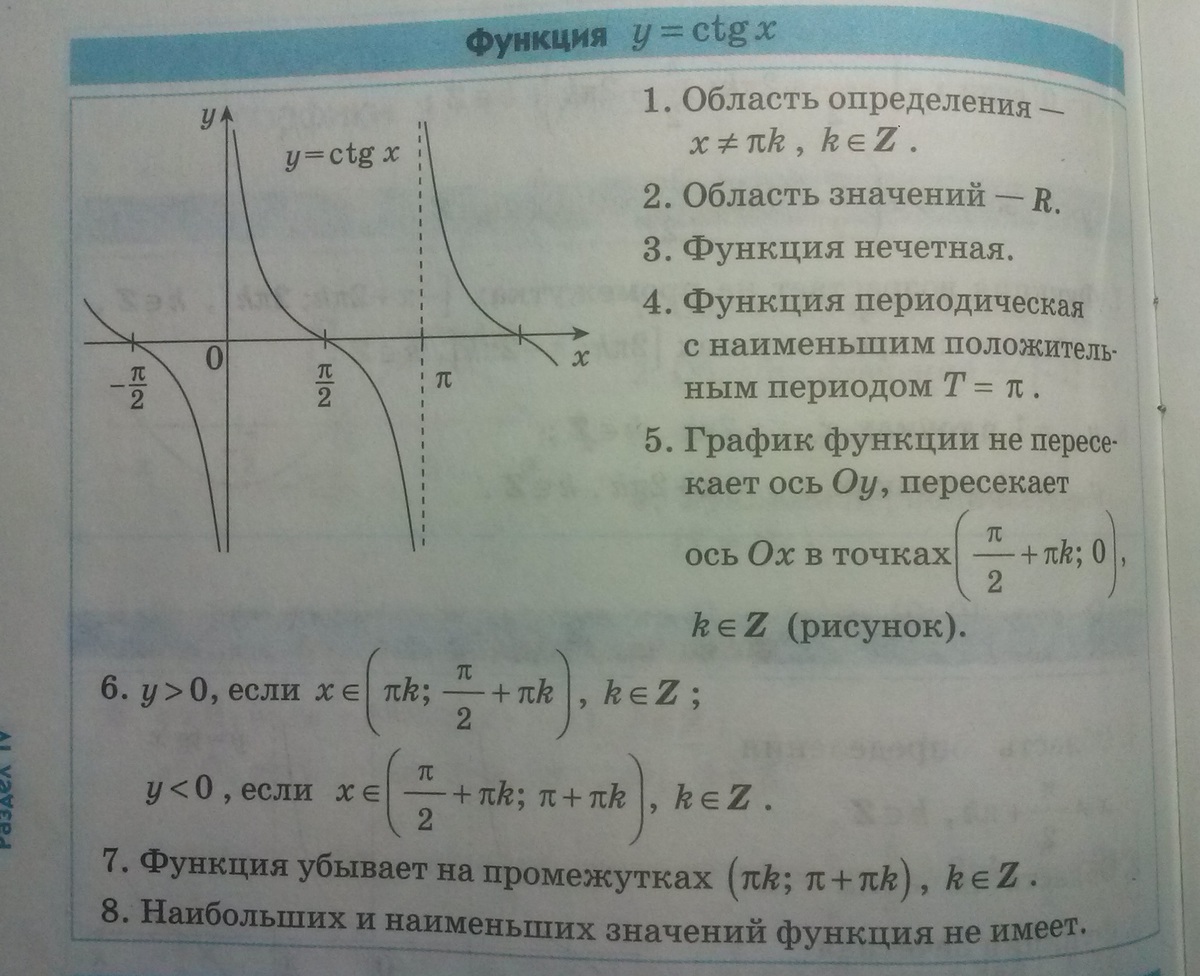
График функции y=tg x
Графики функций, в том числе, тригонометрических, в алгебре могут быть использованы при решении уравнений, неравенств, при решении других заданий.
Источник: http://www.algebraclass.ru/grafik-tangensa/
Урок "Функции y = tgx, y = ctgx, их свойства и графики"
- В этом видеуроке рассмотрены свойства функций у = tgx, y = ctgx, показано, как построить их графики.
- Видеоурок начинается с рассмотрения функции у = tgx.
- Выделены свойства функции.
1) Областью определения функции у = tgxназываются все действительные числа, за исключением х = π/2 +2 πk. Т.е. на графике нет точек, которые принадлежат прямой х = π/2 и х = – π/2, а также х = 3π/2 и так далее (с той же периодичностью).
Значит, график функции у = tgxбудет состоять из бесконечного множества ветвей, которые будут находиться в промежутках между прямыми х = –3π/2 и х = –π/2 , х = –π/2 и х = π/2 и так далее.

2) Функция у = tgxявляется периодической, где основной период равенπ. Это подтверждает равенство tg (x – π)=tg x = tg (x + π).Эти равенства изучались ранее, автор предлагает ученикам вспомнить их, указывая, что для любого допустимого значения tсправедливы равенства:
tg (t + π) = tg t, и ctg (t + π) =ctg t. Следствием этих равенств является то, что, если построена одна ветвь графика функции у = tgxв промежутке между прямыми х = –π/2 и х = π/2 , то остальные ветви можно получить путем сдвига этой ветви по оси х на π, 2π и так далее.
3) Функция у = tgxявляется нечетной, т.к. tg (–x) = – tg x.
Далее перейдем к построению графика функции у = tgx. Как следует из свойств функции, описанных выше, функция у = tgx периодическая и нечетная. Поэтому достаточно построить часть графика – одну ветвь в одном промежутке, а затем воспользоваться симметрией для переноса.
Автор приводит таблицу, в которой рассчитываются значения tgx при определенных значениях xдля более точного построения графика. Данные точки отмечаются на оси координат и соединяются плавной линией. Т.к. график симметричен относительно начала координат, то строится такая же ветвь, симметричная началу координат.
В результате получаем одну ветвь графика у = tgx. Далее с помощью сдвига по оси х наπ, 2 πи так далее получается график у = tgx.
- График функции у = tgx называется тангенсоида, а три ветви графика, показанные на рисунке – главные ветви тангенсоиды.
- 4) Функция у = tgx на каждом из промежутков (– + ; + ) возрастает.
- 5) График функции у = tgx не имеет ограничений сверху и снизу.
- 6) Функция у = tgx не имеет наибольшего и наименьшего значения.
7) Функция у = tgx непрерывна на любом промежутке (-–π/2+π;π/2+π). Прямая π/2+π называется асимптотой графика функции у = tgx, т.к. в этих точках график функции прерывается.
8) Множеством значений функции у = tgxназываются все действительные числа.
Далее в видеоуроке дается пример: решить уравнение с tgx. Для решения построим 2 графика функции у и найдем точки пересечения этих графиков: это бесконечное множество точек, абсциссы которых отличаются на πk. Корнем данного уравнения будет х = π/6 +πk.
Рассмотрим график функции у = ctgx. График функции можно построить двумя способами.
Первый способ предполагает построение графика аналогично построению графика функции у = tgx. Построим одну ветвь графика функции у = сtgxв промежутке между прямыми х = 0и х = π. Затем с помощью симметрии и периодичности построим другие ветви графика.
Второй способ более простой. График функции у = сtgxможно получить путем преобразования тангенсоиды с помощью формулы приведения сtgx = – tg (x + π/2).
Для этого сдвинем одну ветвь графика функции у = tgxвдоль оси абсцисс на π/2вправо. Остальные ветви получаем путем сдвига этой ветви по оси х наπ, 2π и так далее.
График функции у = ctgx называется также тангенсоида, а ветвь графика в промежутке (0;π) – главная ветвь тангенсоиды.
ТЕКСТОВАЯ РАСШИФРОВКА:
Мы рассмотрим свойства функции у = tg x ( игрек равно тангенс икс), у = ctg x( игрек равно котангенс икс), построим их графики. Рассмотрим функцию y = tgx
Прежде, чем строить график функции у = tg x, запишем свойства этой функции.
СВОЙСТВО 1. Областью определения функции у = tg x являются все действительные числа, кроме чисел вида х = + πk (икс равен сумме пи на два и пи ка).
Это значит, что на графике этой функции нет точек, которые принадлежат прямой х = ( получаем, если k= 0 ка равно нулю) и прямой х = ( икс равно минус пи на два ) (получаем, если k= — 1 ка равно минус одному), и прямой х = ( икс равно три пи на два ) (получаем, если k= 1 ка равно одному) и т. д. Значит график функции у = tg x будет состоять из бесконечного множества ветвей, которые будут находиться в промежутках между прямыми. А именно в полосе между х = и х =- ; в полосе х =- и х = ; в полосе х = и х = и так до бесконечности.
СВОЙСТВО 2. Функция у = tg x является периодической с основным периодом π. (Так как справедливо двойное равенство
tg( x– π) = tgx = tg (x+π) тангенс от икс минус пи равен тангенсу икс и равен тангенсу от икс плюс пи). Это равенство мы рассматривали при изучении тангенса и котангенса. Напомним его:
- Для любого допустимого значения t справедливы равенства:
- tg (t + π)= tgt
- ctg (t + π) = ctgt
- Из этого равенства следует, что, построив ветвь графика функции у = tg x в промежутке от х =- и х = , мы получим остальные ветви путем сдвига построенной ветви по оси Х на π, 2π, и так далее.
СВОЙСТВО 3. Функция у = tg x является нечетной функцией, так как справедливо равенство tg ( — x) = — tg x.
Построим график функции у = tg x
Так как эта функция периодическая, состоит из бесконечного множества ветвей (в полосе между х = и х = , а также в полосе между х = и х = и т.д.) и нечетная, то построим по точкам часть графика на промежутке от нуля до пи на два (), затем воспользуемся симметрией начала координат и периодичностью.
Построим таблицу значений тангенса для построения графика.
Находим первую точку: зная, что при х = 0 tg x = 0( икс равном нулю тангенс икс тоже равен нулю); следующая точка: при х = tg x = ( икс равном пи на шесть тангенс икс равен корень из трех на три); отметим следующие точки: при х = tg x = 1 (икс равном пи на четыре тангенс икс равен единице), а при х = tg x = ( икс равном пи на три тангенс икс равен корню квадратному из трех). Отметив полученные точки на координатной плоскости и соединим их плавной линией (рис. 2).
Так как график функции симметричен относительно начала координат, то построим такую же ветвь симметрично начала координат. (рис.3).
И, наконец, применив периодичность, получим график функции у = tg x.
Мы построили ветвь графика функции у = tg x в полосе от х =- и х = . Строим остальные ветви путем сдвига построенной ветви по оси Х на π, 2π, и так далее.

- Построенный график называется тангенсоида.
- Изображенную на рисунке 3 часть тангенсоиды называют главной ветвью тангенсоиды.
- На основании графика запишем еще свойства этой функции.
СВОЙСТВО 4. Функция у = tg x возрастает на каждом из промежутков (от минус пи на два плюс пи ка до пи на два плюс пи ка).
СВОЙСТВО 5. Функция у = tg x не ограничена ни сверху, ни снизу.
СВОЙСТВО 6. Функция у = tg x не имеет ни наибольшего, ни наименьшего значений.
СВОЙСТВО 7. Функция у = tg x непрерывна на любом интервале вида ( от минус пи на два плюс пи ка до пи на два плюс пи ка).
Прямая вида х = + πk (икс равно сумме пи на два и пи ка) является вертикальной асимптотой графика функции, так как в точках вида х = + πk функция терпит разрыв.
СВОЙСТВО 8. Множеством значений функции у = tg x являются все действительные числа, то есть ( е от эф равно промежутку от минус бесконечности до плюс бесконечности).
ПРИМЕР 1. Решить уравнение tg x = (тангенс икс равен корень из трех на три).
Решение. Построим в одной системе координат графики функций у = tg x
(игрек равен тангенсу икс) и у = ( игрек равен корню из трех, деленному на три).
Получили бесконечно много точек пересечения, абсциссы которых отличаются друг от друга на πk ( пи ка).Так как tg x = при х = , то абсцисса точки пересечения на главной ветви равна ( пи на шесть).
- Все решения данного уравнения запишем формулой х = + πk ( икс равно пи на шесть плюс пи ка).
- Ответ: х = + πk.
- Построим график функции у = сtg x.
- Рассмотрим два способа построения.
- Первый способ аналогичен построению графика функции у = tg x.
Так как эта функция периодическая, состоит из бесконечного множества ветвей (в полосе между х = 0 и х =π , а также в полосе между х =π и х = 2π и т.д.) и нечетная, то построим по точкам часть графика на промежутке от нуля до пи на два (), затем воспользуемся симметрией и периодичностью.
- Воспользуемся таблицей значений котангенса для построения графика.
- Отметив полученные точки на координатной плоскости и соединим их плавной линией.
- Так как график функции симметричен относительно , то построим такую же ветвь симметрично .
- Применим периодичность, получим график функции у = сtg x.
Мы построили ветвь графика функции у = сtg x в полосе от х = 0 и х =π. Строим остальные ветви путем сдвига построенной ветви по оси x на π, – π, 2π, – 2π и так далее.
Второй способ построения графика функции у =сtg x.
Получить график функции у =сtg x проще всего с помощью преобразования тангенсоиды, используя формулу приведения ( котангенс икс равно минус тангенс от суммы икс и пи на два).

При этом сначала, сдвинем ветвь графика функции у =tg x вдоль оси абсцисс на вправо, получим
у = tg (x+ ), а затем выполняем симметрию полученного графика относительно оси абсцисс. В результате получится ветвь графика функции у =сtg x (рис.4). Зная одну ветвь, можем построить весь график используя периодичность функции. Строим остальные ветви путем сдвига построенной ветви по оси x на π, 2π, и так далее.
График функции у =сtg x называется тоже тангенсоида, как и график функции у =tg x. Ветвь, которая заключена в промежутке от нуля до пи, называют главной ветвью графика функции у =сtg x.
Источник: https://urokimatematiki.ru/urok-funkcii-y-tg-y-ctg-ih-svoystva-i-grafiki-852.html
презентация потеме Функция тангенса, ее график и свойства. презентация к уроку по алгебре (10 класс) по теме
Слайд 1
Функция у = tg х и построение ее графика. .
Слайд 3
Определяем цели учебной деятельности 1.Выделите слова и словосочетания, встречаемые впервые. 2.Определите, знаете ли Вы точное значение этих слов, а также тех слов и словосочетаний, которые уже встречались Вам, но точные их значения и определения остаются Вам пока неизвестными.
Слайд 4
Определяем цели учебной деятельности 3 . Какие новые определения и значения каких понятий необходимо будет усвоить в рамках изучения данной темы? 4. Какие умения нужно будет выработать? 5. Какие правила, алгоритмы, способы действий Вам неизвестны , и для решения каких задач они Вам будут нужны?
- Слайд 5
- Тангенс.
- Слайд 6
Предполагаемые цели учебной деятельности учеников 1. Определение функции тангенса, свойств этой функции 2.Построение графика функции тангенс по таблице значений и тем свойствам, которые известны для тангенса (алгоритм построения). Узнать, н а какой линии находятся тангенсы углов.
Слайд 7
Находим ответы на вопросы в учебнике. Стр.17 -стр.18: определение , л иния тангенсов углов, о бласть определения, о бласть значений, с войства тангенса, известные вам на сегодняшний день.
- Слайд 8
- Рисунок 10 из учебника
- Слайд 9
Функция у = tg х. Определение. Числовая функция, заданная формулой у = tg х , называется функцией тангенса. Тангенс угла – отношение ординаты точки на единичной окружности, соответствующей данному углу, к абсциссе этой точки. А где находятся тангенсы углов?
- Слайд 10
- Тригонометрический круг
- Слайд 11
- диктант a = 185 градусов a = – 185 градусов a = 102 a = – 102 a = 250 a = – 250 a = 375 a = 145 a = – 145 a = 225 a = – 315 a = 210 a = 590 a = – 15 1Углом какой четверти является угол a , если:
- Слайд 12
диктант 2. Вычислите : 1 вариант. cos 180 + 5sin 90 sin 180 – 3 cos 0 5ctg 90 – 7tg 180 sin 60 + cos 30 2 вариант. cos 0 + 3sin 90 sin 270 – 2cos 180 6tg 180 + 2ctg 90 1 + ctg 270 – 5 tg 360
Слайд 13
Нормы оценок 1.Все задания верны – оценка «5» 2. 1-2 ошибки – оценка «4» 3. 3- 5 ошибок – оценка «3» 4. более 5 ошибок – беру дополнительное домашнее задание. Успехов в учебе!
Слайд 14
Ответы к диктанту. 1вариант. 1. III,II,II,III,III,II,I. 2. 4,-3,0. 2 вариант. 1.II,III,III,I,III,III,IV. 2. 0,2,4. Задание . Заполнить в тетради таблицу значений для построения графика у = tg х. Работа в парах.
Слайд 15
Построение графика. Составляем план построения графика, пользуясь учебником.
Слайд 16
План построения графика. 1 . Правильно выбери единичный отрезок. 2. Н айди область определения. 3 Проведи прямые у = π/ 2 + π n , где n принадлежит целым числам. 4. Построй график. Работаем в парах.
- Слайд 17
- Линия тангенса
- Слайд 18
- График функции в 1 четверти у = tg x x y 0 1
- Слайд 19
- у = tg x х у y = tg x
- Слайд 20
Выполнение заданий. №37(В),33(г). Устно составить план выполнения задания, обговорить в парах. Рефлексия. Ответьте на вопросы: Какие новые знания вы приобрели на этом уроке? Какие новые умения? Все ли цели урока были достигнуты? .
Слайд 21
Домашняя работа. 1. Построить по аналогичному график функции котангенс. 2.Уметь доказывать по рис 10 из учебника, что касательная к числовой окр ., проведенная в точке (1,0), является линией тангенсов.
36( а,б,в ),38(а), 39( а,в,г ) Творческое задание. По рис.11учебника, доказать, что касательная прямая, проведенная в точке (0,1) к числовой окружности, является линией котангесов . Спасибо за урок.
Слайд 22
Спасибо за урок.
Источник: https://nsportal.ru/shkola/algebra/library/2013/11/04/prezentatsiya-poteme-funktsiya-tangensa-ee-grafik-i-svoystva




