Продольные и поперечные волны в физике

• Кто волны, вас оставил,
• Кто оковал ваш бег могучий,
• Кто в пруд безмолвный и дремучий
• Поток мятежный обратил?

А. С. Пушкин

1. В прошлых темах говорилось о колебательных процессах.
2. Движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях, называют механическим колебательным движением.
3. Оказывается, помимо просто колебательного процесса в узкой области пространства, возможно еще и распространение этих колебаний в среде.

Можно наблюдать рябь на поверхности озера или реки. Если бросить камень в воду, то от него пойдут круги. Подобные процессы распространения возмущения представляют собой волну.

Волна — это изменение состояния среды, распространяющееся в пространстве и времени.

Перейдем к обсуждению этого распространения. Прежде, чем обсудить возможность существования колебаний в среде, необходимо определиться с тем, что такое упругая среда.

Среда называется упругой, если между ее частицами существуют силы взаимодействия, препятствующие какой-либо деформации этой среды.

Рассмотрим следующий пример, на поверхность воды в сосуде поместим легкий поплавок. Заставив его совершать колебания, можно увидеть, что от него по воде идут круги — волны.

Ког­да какое-либо тело совершает колебания в упругой среде, то оно воздей­ствует на частицы среды, прилегающие к телу, и заставляет их совер­шать вынужденные колебания. Среда вблизи колеблющегося тела дефор­мируется, и в ней возникают упругие силы. Эти силы воздействуют на все более удаленные от тела частицы среды, выводя их из положения равновесия.

Постепенно все частицы среды вовлекаются в колебательное движение. Таким образом, частицы, которые прилегают вплотную к поплавку, будут повторять его движение, т.е. будут совершать колебания. Поскольку эти частицы взаимодействуют с другими более удаленными от поплавка частицами, то они также будут совершать колебания, но с некоторым запаздыванием.

Таким образом, колебание будет распространяться по всем направлениям.

Подобное волновое движение можно наблюдать в длинной пружине, расположенной горизонтально. Если один конец пружины закрепить, а другой слегка сжимать и отпускать, то по пружине будет распространяться волна.

При сжатии пружины возникает сила упругости, которая заставляет витки пружины разжиматься. Витки, подобно маятнику, колеблются возле своих положений равновесия.

Эти колебания постепенно передаются от витка к витку вдоль всей пружины.

Во всех этих примерах источником волн являются различные тела. Их называют источниками волн. Т.е., источники волн — это тела, которые вызывают распространяющиеся в среде упругие волны. Это, например, колеблющиеся камертоны, струны музыкаль­ных инструментов.

Упругими волнами называются механические возмущения, производимые источниками, которые распространяются в упругой среде. Упругие волны в вакууме распространяться не могут.

Далее будут рассматриваться только бегущие волны. Основное свойство бегущих волн заключается в том, что они, распространяясь в пространстве, переносят энергию без переноса вещества. Пронаблюдаем это на опыте.

В сосуд с водой, в котором находится поплавок, поместим второй поплавок. После того как первый поплавок начнет совершать колебания, начнет колебаться и второй поплавок, благодаря энергии полученной от волны. При этом сам поплавок будет оставаться на месте.

Значит, частицы воды не переносятся волной, т.е. не происходит переноса вещества.

При описании волнового процесса среду считают сплошной и непре­рывной, а ее частицами являются бесконечно малые элементы объема, в которых находится большое количество молекул.

Геометрическое место точек среды, колеблющихся в одинаковых фа­зах, образует волновую поверхность.

Волновую поверхность, отделяющую колеблющиеся частицы среды от частиц, еще не начавших колебаться, называют фронтом волны. В за­висимости от формы фронта волны различают волны плоские, сфери­ческие и др.

Так, например, в плоской волне волновые поверхно­сти представляют собой плоскости, пер­пендикулярные к направлению распрост­ранения волны.

В сферической волне волновые поверх­ности представляют собой концентричес­кие сферы. Сферическую волну может создать пульсирующий в однородной уп­ругой среде шар. Такая волна распрост­раняется с одинаковой скоростью по всем направлениям.

Линия, проведенная перпендикулярно волновому фронту в направлении распро­странения волны, называется лучом. Луч указывает направление распространения волны.

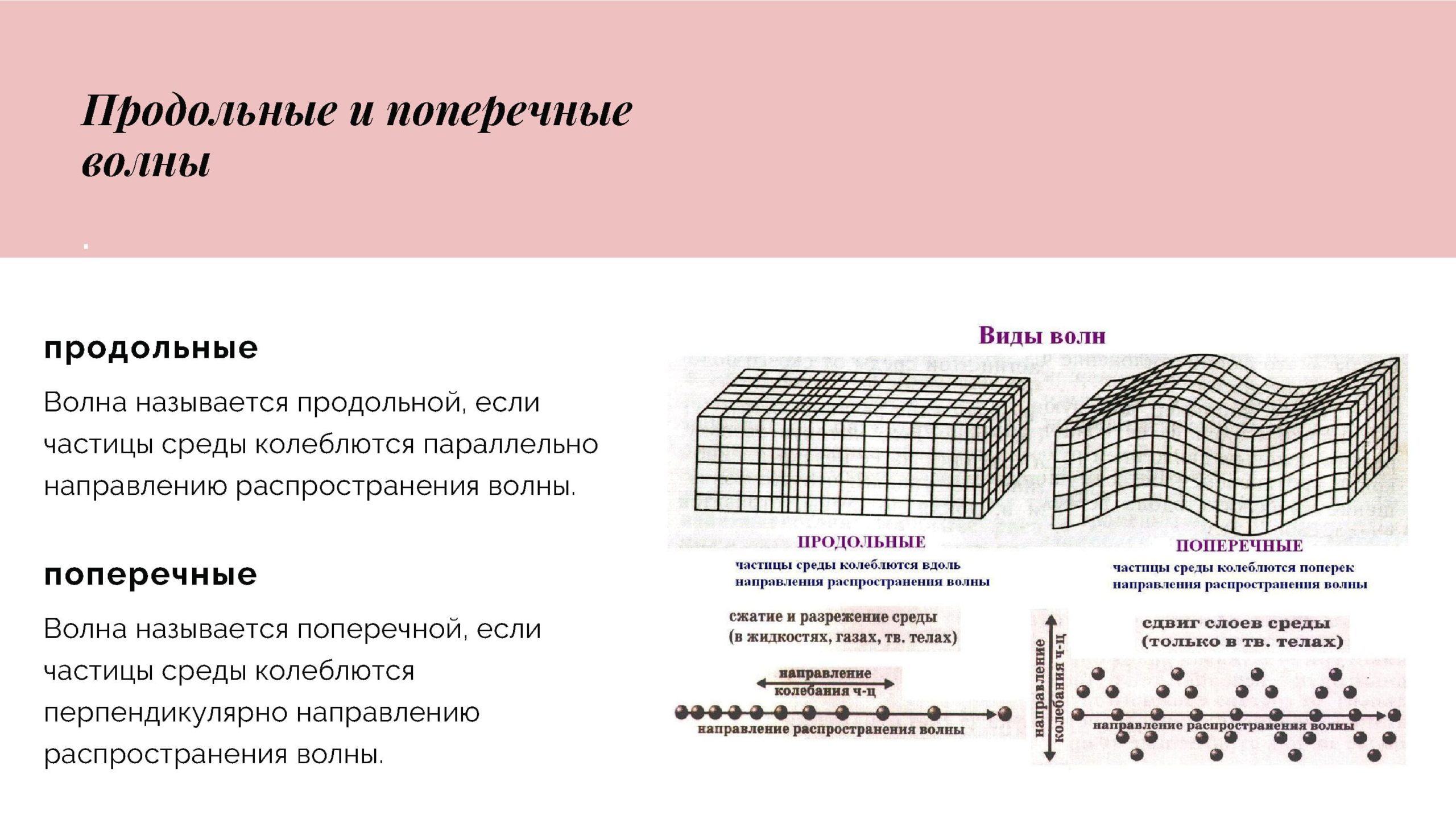
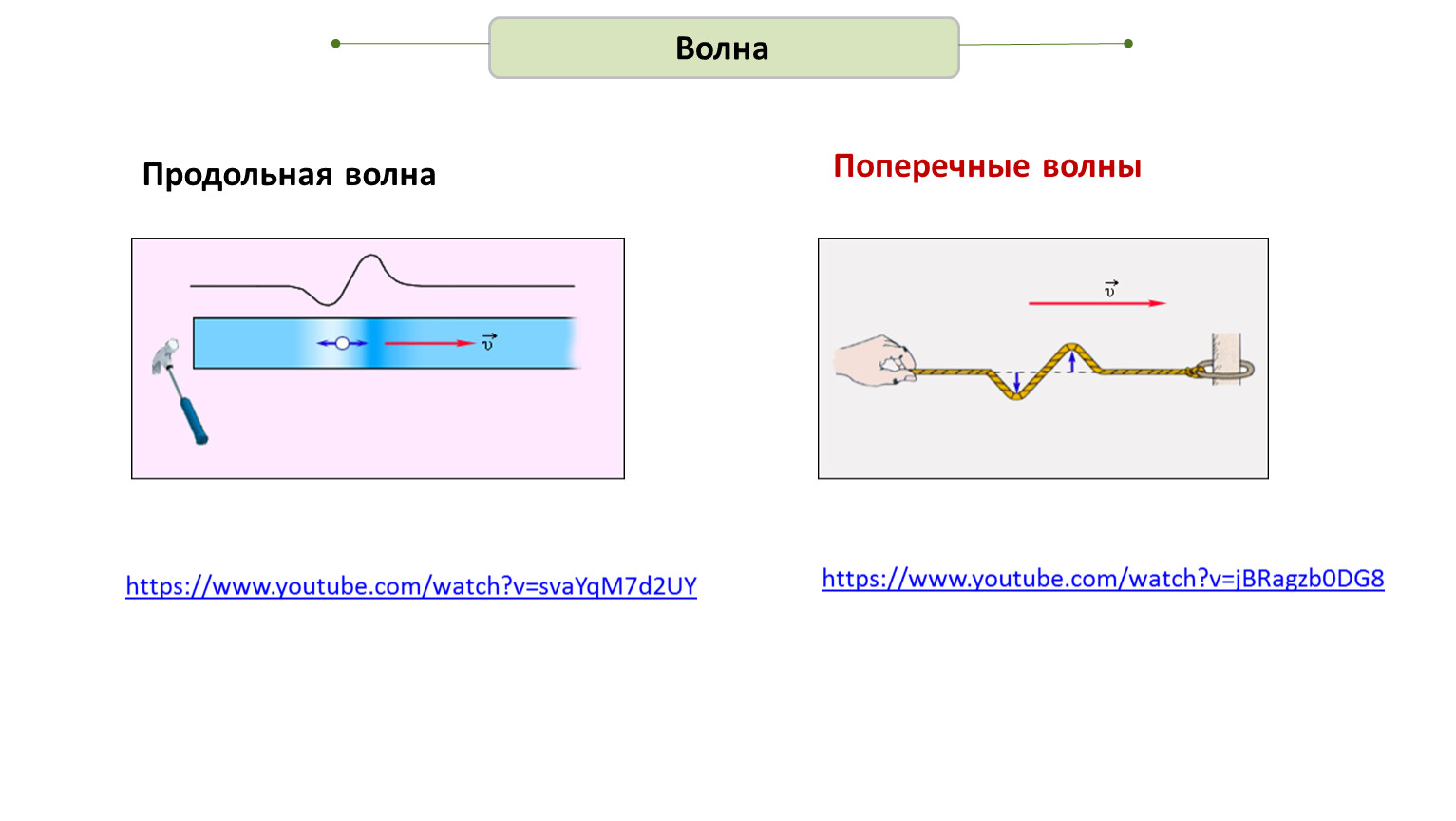
Все волны делятся на два вида — продольные и поперечные.

Волна называется поперечной, если частицы среды совершают колеба­ния в направлении, перпендикулярном к направлению распространения волны.

Поперечная волна распрост­раняется, например, вдоль натянутого го­ризонтального резинового шнура, один из концов которого закреплен, а другой приведен в вертикальное колебательное движение.

Волна называется продольной, если частицы среды совершают колебания в направлении распространения волны. Продольная волна распрост­раняется, например, вдоль натянутой го­ризонтальнойпружины.

Распространение продольных и поперечных волн можно описать с помощью модели, в которой частицы среды представлены в виде совокупности шариков и пружинок.

В продольных волнах шарики испытывают смещение вдоль цепочки, а пружинки растягиваются или сжимаются. Продольные волны могут распространяться в любых средах — твердых, жидких и газообразных.

Если же один или несколько шариков сместить в направлении, перпендикулярном цепочке, то в результате по ней побежит поперечная волна. Поперечные волны могут существовать только в твердых средах, т.к. смежные слои жидкости или газа могут свободно скользить друг по другу без проявления упругих сил.

• Основные выводы:
• – Волна — это изменение состояния среды, распространяющееся в пространстве и времени.
• – Источники волн — это тела, которые вызывают распространяющиеся в среде упругие волны.
• – Основное свойство волн заключается в том, что они, распространяясь в пространстве, переносят энергию без переноса вещества.
• – Все волны делятся на два вида — продольные и поперечные.

– Волна называется поперечной, если частицы среды совершают колеба­ния в направлении, перпендикулярном к направлению распространения волны.Такие волны могут распространяться в любых средах — твердых, жидких и газообразных.

– Волна называется продольной, если частицы среды совершают колебания в направлении распространения волны. Продольные волны могут существовать только в твердых средах, т.к. смежные слои жидкости или газа могут свободно скользить друг по другу без проявления упругих сил.

Источник: https://videouroki.net/video/31-rasprostranieniie-koliebanii-v-uprughikh-sriedakh-prodol-nyie-i-popieriechnyie-volny.html

1.5.4 Поперечные и продольные волны. Скорость распространения и длина волны. Интерференция и дифракция волн

Видеоурок: Длина волны — Физика в опытах и экспериментах

Лекция: Поперечные и продольные волны. Скорость распространения и длина волны. Интерференция и дифракция волн

Волны

Любые возмущения среды, которые распространяются с некоторой скоростью, называются волнами.

Начнем с тех волн, которые мы постоянно видим на воде. Если на систему, в данном случае жидкость, подействовать некоторой силой, то она выйдет из состояния равновесия. Начнется распространения волн.

Волны на воде — колебания пластов воды. В данном случае, если течения отсутствуют, то происходит просто поднятие или опускание жидкости. Существует ошибочное мнение, что волны перемещают слои жидкости.

На самом деле колебания происходят только по горизонтали.

Упругие волны делятся на:

• Продольные — когда колебания происходят по направлению движения волны.
• Поперечные — колебания, направленные перпендикулярно к направлению среды.

Средой для распространения продольной волны может служить твердое, газообразное или жидкое тело. Поперечная же распространяется только в твердом теле.

Расстояние между двумя соседними максимумами или минимумами амплитуды называется длиной волны. 

Эта величина обозначается буквой лямбда, единицей измерения является метр (м).

Скорость, с которой волна распространяется в среде, называется скоростью колебания.

Благодаря тому, что атомы и молекулы в твёрдых телах находятся достаточно близко друг к другу, они лучше взаимодействуют друг с другом, что приводит к большей скорости волны. Отсюда можно сделать вывод — чем более плотная среда, тем быстрее в ней распространяются волны.

Интерференция

Процесс наложения волн, находящихся в одинаковой фазе или противофазе, в результате чего происходит достижение максимумов и минимумов амплитуды, называется интерференцией.

Чтобы интерференция произошла, в обязательном порядке волны должны быть когерентными. Это значит, что они должны испускаться с одинаковой частотой и в одинаковой фазе.

Дифракция

Если Вы находитесь в комнате, а Ваша мама зовет Вас кушать с кухни, сможете ли Вы услышать приглашение к столу? Естественно. Звук — это также колебание среды, то есть волны, так как между Вами и кухней находятся стены, то можно сделать вывод, что волна может огибать преграду.

Процесс огибания волнами преград, называется дифракцией.

 

Предыдущий урок

Следующий урок

Источник: https://cknow.ru/knowbase/108-tema-154-poperechnye-i-prodolnye-volny-skorost-rasprostraneniya-i-dlina-volny-interferenciya-i-difrakciya-voln.html

Примеры продольных и поперечных волн

Если колебательное движение возбуждают в какой — либо точке среды, то оно распространяется от одной точки к другой в результате взаимодействия частиц вещества. Процесс распространения колебаний называют волной.

Рассматривая механические волны, мы не будем обращать внимание на внутреннее строение среды. Вещество при этом считаем сплошной средой, которая изменяется от одной точки к другой.

Частицей (материальной точкой), будем называть маленький элемент объема среды, размеры которого, много больше, чем расстояния между молекулами.

Механические волны распространяются только в средах, которые обладают свойствами упругости. Силы упругости в таких веществах при небольших деформациях пропорциональны величине деформации.

Основным свойством волнового процесса является то, что волна, перенося энергию и колебательное движение, не переносит массу.

Волны бывают продольные и поперечные.

Продольные волны

Волну называю продольной, в том случае, если частицы среды совершают колебания в направлении распространения волны.

Продольные волны распространяются в веществе, в котором возникают силы упругости, при деформации растяжения и сжатия в веществе в любом агрегатном состоянии.

При распространении продольной волны в среде возникают чередования сгущений и разрежений частиц, перемещающихся в направлении распространения волны со скоростью ${
m v}$.

В твердых телах скорость распространения продольных волн больше, чем скорость поперечных волн.

Волны в жидкостях и газах всегда продольные. В твердом теле тип волны зависит от способа ее возбуждения. Волны на свободной поверхности жидкости являются смешанными, они одновременно и продольные и поперечные. Траекторией движения частицы воды на поверхности при волновом процессе является эллипс или еще более сложная фигура.

Акустические волны (пример продольных волн)

Звуковые (или акустические) волны, являются продольными волнам. Звуковые волны в жидкостях и газах представляют собой колебания давления, распространяющиеся в среде. Продольные волны, имеющие частоты от 17 до 20~000 Гц называют звуковыми.

Акустические колебания с частотой ниже границы слышимости называют инфразвуком. Акустические колебания с частотой выше 20~000 Гц называют ультразвуком.

Акустические волны в вакууме распространяться не могут, так как упругие волны способны распространяться только в той среде, где имеется связь между отдельными частицами вещества. Скорость звука в воздухе равна в среднем 330 м/с.

Распространение в упругой среде продольных звуковых волн связано с объемной деформацией. В этом процессе давление в каждой точке среды непрерывно изменяется. Это давление равно суме равновесного давления среды и добавочного давления (звуковое давление), которое появляется в результате деформации среды.

Сжатие и растяжение пружины (пример продольных волн)

Допустим, что упругая пружина подвешена горизонтально на нитях. По одному концу пружины ударяют так, что сила деформации направлена вдоль оси пружины. От удара происходит сближение нескольких витков пружины, возникает сила упругости. Под воздействием силы упругости витки расходятся.

Двигаясь по инерции, витки пружины проходят положение равновесия, образуется разрежение. Некоторое время витки пружины на конце в месте удара будут колебаться около своего положения равновесия. Данные колебания с течением времени передаются от витка к витку по всей пружине.

Аналогично продольная волна распространяется по металлическому стержню, если ударить по его концу с силой, направленное вдоль его оси.

Поперечные волны

Волну называют поперечной волной, если колебания частиц среды происходят в направлениях перпендикулярных к направлению распространения волны.

Механические волны могут быть поперечными только в среде, в которой возможны деформации сдвига (среда обладает упругостью формы). Поперечные механические волны возникают в твердых телах.

Волна, распространяющаяся по струне (пример поперечной волны)

Пусть одномерная поперечная волна распространяется по оси X , от источника волны, находящегося в начале координат — точке О. Примером такой волны является, волна, которая распространяется в упругой бесконечной струне, один из концов которой заставляют совершать колебательные движения. Уравнение такой одномерной волны:

[s=A{cos left[omega t-kx+varphi
ight] }left(1
ight),]

где

[k=frac{2pi }{lambda }=frac{omega }{v}left(2
ight)]

$k$ -волновое число$;; lambda $ — длина волны; $v$ — фазовая скорость волны; $A$ — амплитуда; $omega $- циклическая частота колебаний; $varphi $ — начальная фаза; величина $left[omega t-kx+varphi
ight]$ называется фазой волны в произвольной точке.

Примеры задач с решением

Пример 1

Задание. Какова длина поперечной волны, если она распространяется по упругой струне со скоростью $v=10 frac{м}{с}$, при этом период колебаний струны составляет $T=1 c$?

Решение. Сделаем рисунок.

• Длина волны — это расстояние, которое волна проходит за один период (рис.1), следовательно, ее можно найти по формуле:
• Вычислим длину волны:
• Ответ. $lambda =10$ м

[lambda =Tv left(1.1
ight).] [lambda =10cdot 1=10 (м)]

Пример 2

Задание. Звуковые колебания с частотой $
u $ и амплитудой $A$ распространяются в упругой среде. Какова максимальная скорость движения частиц среды?

1. Решение. Запишем уравнение одномерной волны:
2. Скорость движения частиц среды равна:
3. Максимальное значение выражения (2.2), учитывая область значений функции синус:
4. Циклическую частоту найдем как:
5. Окончательно максимальная величина скорости движения частиц среды в нашей продольной (звуковой) волне равна:
6. Ответ. ${left(frac{ds}{dt}
   ight)}_{max}=2pi A
   u$

[s=A{cos left[omega t-kx+varphi
ight] }left(2.1
ight),] [frac{ds}{dt}=-Aomega {sin left[omega t-kx+varphi
ight] } left(2.2
ight).] [{left(frac{ds}{dt}
ight)}_{max}=left|Aomega
ight|left(2.3
ight).] [omega =2pi
u left(2.4
ight).] [{left(frac{ds}{dt}
ight)}_{max}=2pi A
u .]

Читать дальше: принцип действия гидравлического пресса.

Источник: https://www.webmath.ru/poleznoe/fizika/fizika_118_primery_prodolnyh_i_poperechnyh_voln.php

Разница между поперечными и продольными волнами

поперечный а такжепродольный два разных типа волн.

главное отличие между поперечными и продольными волнами заключается в том, что в поперечных волнах колебания происходят перпендикулярно направлению распространения волны, в то время как в продольных волнах, Колебания происходят параллельно направлению распространения волны.

Что такое поперечные волны

В поперечных волнах происходят колебанияперпендикуляр (нормаль) к направлению распространения волны. Простую демонстрацию можно выполнить, покачивая веревку вверх и вниз. Сама волна будет распространяться вдоль веревки, тогда как отдельные частицы волны колеблются перпендикулярно длине веревки.

Волна в приведенном выше примере являетсямеханический волна — волна проходит через среду (веревку), частицы которой колеблются, чтобы провести волну. Кроме того, поперечные волны включаютэлектромагнитный волны (радиоволны, микроволны, инфракрасный, видимый свет, ультрафиолет, рентгеновские лучи и гамма-лучи — все это электромагнитные волны).

Для распространения электромагнитных волн не требуется среда, т. Е. Они могут проходить в вакууме. Мы получаем энергию от Солнца через электромагнитные волны, излучаемые Солнцем. В электромагнитных волнах нет частиц, которые физически колеблются, чтобы распространять волну в пространстве, но, скорее, это электрическое поле и сопутствующее магнитное поле, которое колеблется.

Колебания поперечной волны могут быть установлены влюбое направление перпендикулярно направлению распространения. Когда все вибрации происходят в одном направлении, волна называетсяполяризованный (поляризованный).

Что такое продольные волны

В продольных волнах колебания происходят параллельно направлению распространения волны.

Наиболее распространенным примером для этих типов волн являются звуковые волны, которые состоят из колеблющихся молекул воздуха.

Поскольку продольные волны могут колебаться только в одном направлении, они не могут быть поляризованы. Диаграмма ниже иллюстрирует разницу между поперечными и продольными волнами:

а) вверху: продольная волна и б) внизу: поперечная волна.

Направление колебаний

Впоперечные волны, Колебания происходят перпендикулярно направлению распространения волны.

Впродольные волныколебания происходят параллельно направлению распространения.

поляризация

• Поперечные волны может быть поляризован.
• Продольные волны не может быть поляризован.
• Изображение предоставлено:
• «Направление колебаний и распространения продольной волны (а) и поперечной волны (метки на немецком языке)» Debianux (собственная работа) [

Источник: https://ru.strephonsays.com/difference-between-transverse-and-longitudinal-waves

Продольные и поперечные волны (стр. 1 из 2)

• РЕФЕРАТ
• на тему:
• «ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ»
• учениця 11 класу
• Мельник Анжела
• ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ

В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д.

Несмотря на отличия, эти волны имеют много общих черт. Волны, рассматриваемый параметр которых (смещение молекул, механическое напряжение, и т.д.) изменяется периодически вдоль оси распространения, называются продольными волнами.

Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными.

Если взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются упругими. К ним относятся звуковые, ультразвуковые, сейсмические и др. волны.

На первой анимации изображён процесс распространения продольной упругой волны в решётке, состоящей из шариков, соединённых упругими пружинками. Каждый шарик колеблется по гармоническому закону в продольном направлении, совпадающем с направлением распространения волны.

Амплитуда каждого шарика одинакова и равна A, а фаза колебаний линейно растёт с увеличением номера шарика на т.е

x0=Asin(t); x1=Asin(t+); x2=Asin(t+2); x3=Asin(t+3); ит.д.

где  -частота волны, t — время, - изменение фазы от шарика к шарику

В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех шариков одинаковы, а фаза линейно изменяется от шарика к шарику

y0=Bsin(t);y1=Bsin(t+); y2=Bsin(t+2); y3=Bsin(t+3);и т.д.

На следующей анимации изображено наложение продольной и поперечной волн равной амплитуды, сдвинутых по фазе на 90 градусов. В результате каждая масса совершает круговые движения. Уравнение движения каждого шарика может быть описано уравнением:

x=Acos(t+); y=Asin(t+)

У волн, наблюдаемых на поверхности жидкости, так называемых поверхностных волн, взаимосвязь между соседними элементами поверхности жидкости при передаче колебаний осуществляется не силами упругости, а силами поверхностного натяжения и тяжести.

Колебания масс в сетке моделируют движение молекул в волне на поверхности жидкости. В случае малой амплитуды волны каждая масса движется по окружности, радиус которой убывает с расстоянием от поверхности.

Массы внизу сетки находятся в покое

.

Волны на поверхности жидкости не являются ни продольными, ни поперечными. Как мы можем видеть на анимации, красный шарик, моделирующий молекулу поверхности жидкости, движется по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой суперпозицию продольного и поперечного движения молекул.

1. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН НА ПОВЕРХНОСТИ ЖИДКОСТИ
2. Интерференция двух линейных волн
3. Рассмотрим волну, возникающую на поверхности жидкости под воздействием колебаний длинного цилиндрического стержня:
4. z =Acos(t
5. где A — амплитуда колебаний цилиндра,  = 2f, f — частота колебаний, t — время.
6. Если волна распространяется без затухания, то любая точка поверхности жидкости будет колебаться с той же амплитудой, что и стержень, но фаза колебаний будет изменяться пропорционально расстоянию от него:
7. z =Acos(tkx

где k = / v, v — скорость распространения волны. В общем случае, волна будет затухать из-за внутреннего трения жидкости и амплитуда колебаний A будет уменьшаться с расстоянием.

Далее рассмотрим случай интерференции волн от двух стержней, вибрирующих с одинаковой частотой. Предположим, что расстояние между стержнями — d. Амплитуда колебаний поверхности жидкости в любой точке с координатой x может быть найдена как сумма двух волн:

• z = Acos(t — kx) + Acos(t + k(x — d))
• Волновое число k входит в вышеуказанную формулу с разными знаками, что соответствует противоположному направлению распространению волн от двух стержней. Эта формула может быть также переписана в виде:
• z = 2Acos(t — kd/2)cos(kx — kd/2)

Полученное выражение описывает интерференцию двух линейных волн, распространяющихся в противоположных направлениях (стоячая волна).

Мы можем видеть из этого выражения, что существуют точки на поверхности жидкости, где волны интерферируют в противофазе и колебания в этих точках отсутствуют (так называемые узлы), и имеются точки, где волны накладываются, усиливая друг друга, и в этих точках колебания происходят с удвоенной амплитудой 2A (пучности).

Узлы возникают в точках, для которых верно равенство cos(kx — kd/2)=0, то есть в точках x= /2 (1/2+n)+d/2, где n — целое число, а  — длина волны. Это означает, расстояние между соседними узлами равно половине длины волны. То же самое утверждение справедливо и для расстояния между максимумами интерференционной картины.

Анимация показывает интерференцию двух волн на поверхности жидкости, возбуждаемых вибрирующими стержнями. Волны распространяются в противоположных направлениях и интерферируют с образованием стоячей волны.

Красный шарик расположен в пучности стоячей волны и колеблется с максимальной амплитудой.

Параллелепипед расположен в узле интерференционной картины и амплитуда его колебаний равна нулю (он совершает лишь вращательные движения, следуя наклону волны).

Круговые волны на поверхности жидкости

Наблюдение волн на поверхности жидкости позволяет изучить и визуально представить многие волновые явления, общие для разных типов волн: интерференцию, дифракцию, отражение волн и т.д.

Рассмотрим круговую волну на поверхности жидкости, создаваемую точечным источником, в качестве которого мы возьмём маленький шарик на поверхности жидкости, колеблющейся в вертикальном направлении с малой амплитудой.

Так как шарик имеет конечные размеры, то каждая его точка, соприкасающаяся с жидкостью, является, по существу, точечным источником волн, наложение которых и даёт действительную волну. Однако на расстоянии, много большем диаметра шарика, этим можно пренебречь и образующиеся волны рассматривать как круговые, т.е.

состоящий из концентрических окружностей. При этом сам шарик принимают за точечный источник волн. Отметим, что плоскую волну всегда можно представить как сферическую, но с бесконечно большим радиусом, т.е. считать центр плоской волны находящимся в бесконечности.

Интерференция волн от двух точечных источников

Рассмотрим теперь два маленьких шарика, колеблющихся на поверхности жидкости. Каждый из шариков возбуждает волну. Налагаясь, эти волны дают интерференционную картину, показанную на анимации. Рассмотрим уравнение, описывающее интерференционную картину.

1. Если пренебречь затуханием, то волна от каждого шарика может быть записана следующим образом:
2. s1=A1cos(t -kr1); s2=A2cos(t — kr2);
3. где A1 и A2 — амплитуды волн, r1 и r2 — расстояния соответственно от первого и второго шарика, k=  / v, v — скорость распространения волн.
4. Так как разность =r2 -r1 много меньше, чем каждое из расстояний r1 и r2, мы можем положить A= A1 = A2. В этом приближении наложение волн s1 и s2 описывается следующим выражением:
5. s = s1 + s2 = 2Acos[ k(r2 — r1)/2 ] cos[t — k(r1 + r2)/2 ]

Из этого выражения видно, что в точках, для которых r2 -r1 = (1/2+n) , поверхность жидкости не колеблется. Эти узловые точки (линии) отчётливо видны на анимации.

Интерференция круговой волны в жидкостис её отражением от стенки

Рассмотрим точечный источник волн на поверхности жидкости (колеблющийся шарик) и полностью отражающую стенку, установленную в на некотором расстоянии от него.

Если расстояние от источника до стенки кратно целому числу полуволн, то исходная круговая волна будет интерферировать с волной, отражённой от стенки, создавая в волновой ванне интерференционную картину, как показано на анимации.

Согласно принципу Гюйгенса, отражённая волна совпадает с той, которая бы возбуждалась фиктивным точечным источником, расположенным по другую сторону стенки симметрично реальному источнику круговых волн.

При этом если расстояние от источника до стенки кратно целому числу полуволн, то справа от источника на оси соединяющей фиктивный и реальный источник разность фаз будет кратна целому числу волн и круговая волна накладывается в фазе с волной, отражённой от стенки, увеличивая высоту гребней в интерференционной картине.

Источник: https://mirznanii.com/a/321744/prodolnye-i-poperechnye-volny