Уравнение неразрывности потока жидкости в физике

При рассмотрении динамики движения жидкости или газа можно не следить за конкретной точкой среды, а следить за конкретной точкой пространства и фиксировать в таких точках направление и величину скорости различных частиц в данный момент времени.

Таким образом, в каждой точке пространства можно получить некоторый вектор, имеющий определённую величину и направление. Такая картина называется полем скоростей.

В этом поле скоростей можно провести некоторые линии, линии тока (так же, как проводят силовые линии в электрическом или гравитационном полях) (см. рис .1).

Линия тока (на рис. 1 выделены жёлтым) – линия в пространстве, направление касательной к которой в данный момент времени в каждой точке совпадает с направлением вектора скорости в этой точке.

 Рис. 1. Линии тока в поле скоростей

Если сделать мгновенное отображение, то можно поле скоростей заменить линиями тока.

В том случае, когда скорости в данной точке пространства не меняются со временем, такое движение называют стационарным движением жидкости или газа.

В этом случае картина линий тока не будет зависеть от времени, она будет заморожена.

Линия тока в данном случаи будет представлять собой траекторию движения отдельной частицы, которая будет двигаться в каждый момент времени в направлении касательных к этой линии.

 Рис. 2. Трубка тока

При стационарном течении жидкости или газа из стационарных линий тока можно построить поверхность такой формы, которая называется трубкой тока (см. рис. 2).

Эта трубка – мысленно выделенная труба, по которой течёт жидкость или газ (далее будет рассматриваться движение жидкости именно в такой трубе).

Если за определённое время некоторая масса жидкости перетекла через поверхность сечения такой трубы , то такое же количество жидкости должно перетечь через сечение трубы , так как с течением времени полная масса жидкости в этом объёме, выделенным двумя сечениями, меняться не должна.

Выберем сечения  и  настолько маленькими, то есть трубку тока настолько тонкой, что в каждом её сечении скорость () можно считать одинаковой. Тогда можно вычислить количество жидкости, перетекающей за определённой время через поверхность  и .

Также можно вычислить массу, которая перешла через поверхность  за время t: .

• Если рассматривать несжимаемые жидкости, то плотность вещества в сечении  совпадает с плотностью вещества в сечении .
• Следовательно, получаем следующее соотношение: .

То есть для несжимаемой жидкости, произведение скорости на площадь поперечного сечения трубки тока одинаково вдоль всей трубки:  – условие неразрывности. Это означает, что, чем меньше поперечное сечение, тем больше скорость.

Динамика движения реальной жидкости очень сложная, однако в некоторых случаях можно пренебречь вязкостью жидкости, то есть наличием трения между различными слоями жидкости.

В этом случае при движении жидкости не выделяется тепло, то есть сохраняется механическая энергия.

Рассмотрим энергетические соотношения при движении идеальной несжимаемой жидкости. Выделяем некоторую трубку тока, ограниченную сечениями  и  (см. рис. 3). За некоторое время  масса жидкости, заключённой между сечениями и , сместится. Сечение  перейдёт в сечение , а  – в .

Рис. 3. Трубка тока

Рассматриваем не только очень маленькие сечения трубки тока, но и очень маленькие промежутки времени, в течение которых сечения сместятся на очень маленькую величину. Будем пренебрегать изменением площади сечений, изменением высоты, скорости и давления на этих сечениях. С учётом этих данных рассчитаем работу внешних сил над данным объёмом жидкости. Эта работа складывается из таких работ:

1. 1) Внешняя часть жидкости давит на сечение с силой , поэтому совершает работу при перемещении этого сечения.
2. 2) Внешняя часть жидкости давит на сечение  с силой  и совершает отрицательную работу при перемещении этого сечения.
3. Также меняется кинетическая и потенциальная энергия жидкости.

Для того чтобы легче было это понять, рассмотрим объём жидкости, заключённый между сечениями  и . Энергия, масса, скорость, давление и остальные характеристики этого объёма не изменились в силу стационарности движения. Поэтому вся работа внешних сил привела к тому, что энергия части жидкости между  и  переместилась в часть между  и  с ниже посчитанными изменениями:

• Вычислим изменение энергии рассмотренного отрезка трубки тока (изменение энергии части жидкости между  и  по сравнению с энергией между  и ), для этого из энергии конечной отнимаем энергию начальную.
• Изменение потенциальной энергии (потенциальная энергия – это масса (масса – это плотность (), умноженная на объём, а объём в данном случае – это поперечное сечение на длину участка между  и  или  и  ()), умноженная на ускорение свободного падения () и высоту этого участка над некоторым нулевым уровнем):
• .
• Изменение кинетической энергии (масса, умноженная на квадрат скорости и делённая на два): .
• Изменение энергии в соответствии с законом сохранения энергии равно работе внешних сил.

Приравниваем эти величины и переносим слагаемые с одинаковыми индексами в одну сторону. Сократив ,  и  (согласно условию неразрывности ), получаем окончательный результат: .

Сечения  и  были выбраны произвольно, поэтому уравнение можно записать в таком виде: .

Мы получили уравнение Бернулли. Это уравнение утверждает, что сумма физических величин () постоянна вдоль очень узкой трубки тока. В математическом смысле следует устремить сечение этой трубки к нулю, то есть получим линию тока. Следовательно,  вдоль любой линии тока.

1) Определим скорость истечения жидкости из маленького отверстия в большом сосуде с жидкостью. Пусть h – высота верхнего уровня жидкости по отношению к положению отверстия.

Давление над жидкостью и около отверстия равно атмосферному, то есть внешнее давление одинаково везде (). В очень большом сосуде при истечении жидкости из маленького отверстия скорость жидкости можно считать равной нулю ().

Следовательно, в верхней точки жидкости (где высота – h, а ), то есть в левой части уравнения Бернулли, получаем величину .

1. В нижней части около отверстия на глубине h (где , а ), то есть в правой части уравнения Бернулли, получаем величину .
2. Из этого равенства легко найти скорость () истечения жидкости из маленького отверстия: .

2) Измерим давление жидкости с помощью манометра (прибор, который имеет небольшую площадь поверхности, располагается в трубке тока определённым образом). Расположим манометр так, чтобы его поверхность была параллельна линиям тока.

При этом манометр будет показывать давление в жидкости, которая течёт со скоростью v(манометр, расположенный параллельно линиям тока, не будет влиять на эту линию), следовательно, в левой части уравнения Бернулли получаем величину .

Расположим манометр перпендикулярно линиям тока. Такое положение манометра влияет на течение жидкости. Жидкость у поверхности манометра будет останавливаться (обтекать манометр). То есть скорость в точке у поверхности манометра будет равна 0 (), поэтому в правой части уравнения Бернулли получаем величину .

• Такое соотношение используется для определения скорости течения жидкости.
• Домашнее задание

1. Что такое линия тока?
2. Упражнение 16 (21, 24), стр. 478. Учебник: «Физика. Механика. 10 кл.» (см. список рекомендованной литературы)
3. Струя жидкости со скоростью бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление , плотность жидкости .

Список рекомендованной литературы

1. М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. Физика. Механика. 10 кл. Профильный уровень. – М.: Дрофа, 2004.
2. Парфентьева Н., Фомина М. Решение задач по физике: Часть 1. – М.: Мир, 1993.
3. А.В. Пёрышкин, В.В. Крауклис. Курс физики т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Рекомендованные ссылки на ресурсы сети Интернет

1. Clck.ru (Источник).
2. Clck.ru (Источник).
3. Clck.ru (Источник).

Источник: https://interneturok.ru/lesson/physics/10-klass/bmehanika-sistemy-telb/osnovnye-ponyatiya-gidrodinamiki-liniya-toka-trubka-toka-usloviya-nerazryvnosti-neszhimaemosti-zhidkosti-uravnenie-bernulli?konspekt

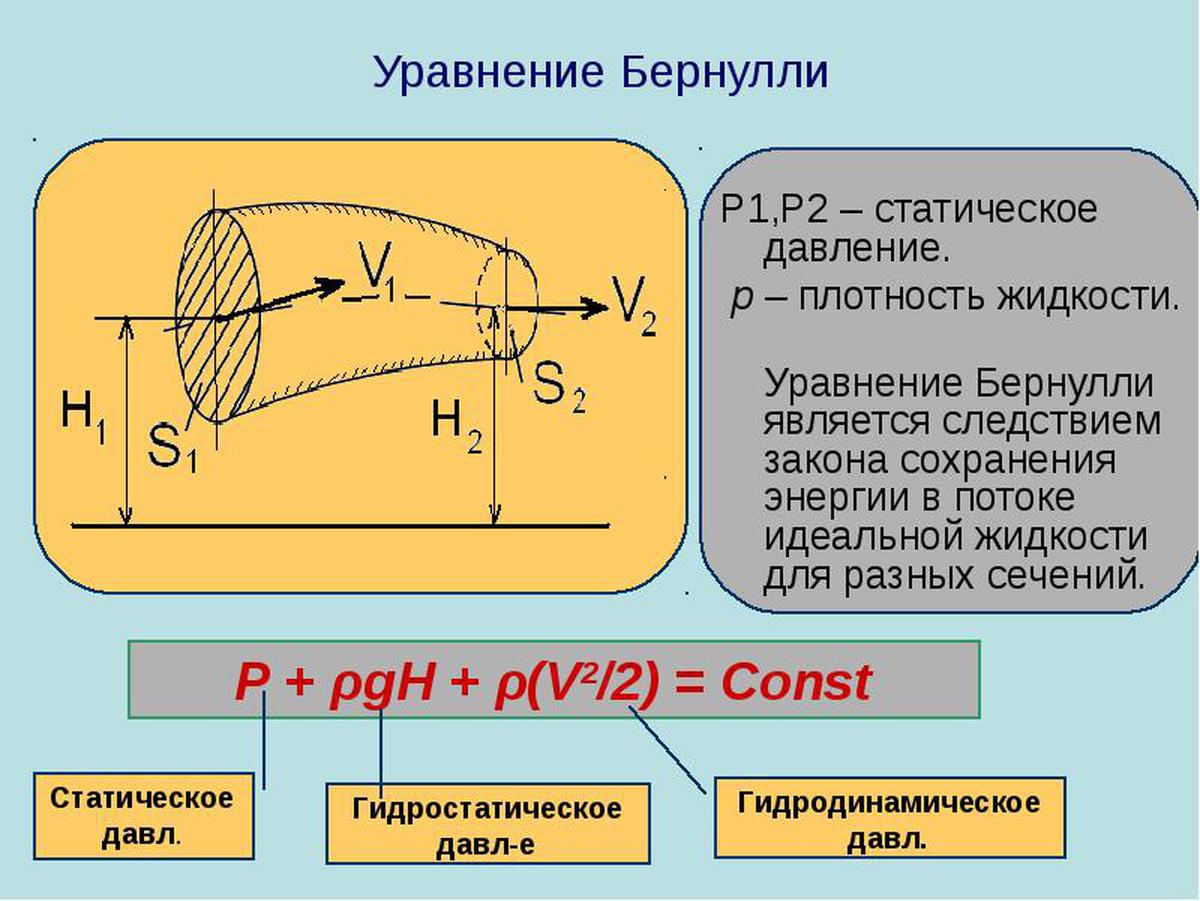
Уравнение Бернулли. Теорема о неразрывности струи

Сегодня решаем задачи на теорему Эйлера о неразрывности струи и вспоминаем уравнение Бернулли.

Уравнение неразрывности струи:

Русло реки в разрезе

Русло реки. Разрез

Здесь – скорость струи в сечении , а   – скорость в сечении . Можно сделать вывод о том, что чем уже трубка, по которой течет жидкость, тем быстрее она течет. Именно поэтому течение реки  быстрее на поверхности, чем в глубине и в середине русла, чем у берега. На рисунке показан разрез русла реки, и синим выделены зоны, где течение быстрее.

• Конечно, деление сечения русла на зоны условно.
• Уравнение Бернулли:
•    

Здесь – плотность жидкости, – ускорение свободного падения, и – высоты элемента жидкости над землей, и – скорости жидкости на этих высотах, и – давления жидкости на этих высотах. Уравнение может быть применено как к жидкой среде, так и к газообразной.

1. Если записать уравнение иначе:
2.    
3. то слева имеем разность давлений. Предположим, высота одинакова, тогда уравнение запишется так:
4.    

Тогда становится понятно, почему при сильном ветре большие стекла могут быть выдавлены изнутри, ведь внутри помещения скорость ветра нулевая. Если среда 1 – улица, а среда 2 – среда внутри помещения, то давление внутри помещения больше давления снаружи, поэтому выдавливание произойдет наружу.

Аналогичные рассуждения можно провести и сделать вывод, что крыши во время урагана срывает по той же причине.

Задача 1. На эффекте Бернулли основано движение роторного судна. На этом корабле вместо парусов имеются огромные вертикальные цилиндры, непрерывно вращающиеся с помощью моторов. Допустим, что дует постоянный южный ветер, а корабль такой конструкции должен плыть на восток. Как должны вращаться цилиндры – по часовой стрелке или против, если смотреть на них сверху?

Роторное судно

Цилиндр сверху

Рассмотрим рисунок. Слева ветер как бы подгоняет цилиндр: скорость ветра складывается со скоростью цилиндра, а справа скорость ветра направлена против скорости цилинда, ветер «тормозит» его вращение.

Тогда согласно уравнению Бернулли возникает положительная разность давлений: давление впереди цилиндра по ходу движения меньше, чем давление позади.

Эта разность давлений и будет подталкивать судно в направлении слева направо, то есть на восток.

Ответ: по часовой стрелке.

Эффект Магнуса – также проявление действия закона Бернулли. Здесь можно посмотреть интересное видео, где показано проявление этого эффекта.

Задача 2. Вода течет по горизонтальной трубе переменного сечения. Скорость течения в горизонтальной части трубы равна 20 см/с. Определить скорость течения воды в узкой части трубы, диаметр которой в 1,5 раза меньше диаметра широкой части.

• Воспользуемся уравнением неразрывности струи:
• Пусть – скорость воды в узкой части трубы и – сечение трубы в узкой части.
• Выразим из него скорость  :
• Сечение трубы – круг, площадь круга в узкой части , в широкой части .
• Тогда:
• Про отношение диаметров нам известно, что
• Тогда можно подставить в нашу формулу числа (только не забудем представить известную скорость в единицах СИ).
• Ответ: скорость воды в узкой части 0,45 м/с

Задача 3. С катера, идущего со скоростью км/ч, опускают в воду изогнутую под прямым углом трубку так, что опущенный конец трубки горизонтален и обращен отверстием в сторону движения. Другой конец трубки, находящийся в воздухе, вертикален. На какую высоту по отношению к уровню воды в озере поднимется вода в трубке? Трением пренебречь.

Скорость нужно представить в единицах СИ: м/с

Скорость воды относительно катера также равна 5 м/с. То есть вода обладает кинетической энергией . Когда вода поднимается в трубку, ее кинетическая энергия преобразуется в потенциальную: .

1. Так как трения нет, то нет и потерь энергии, то есть можем приравнять:
2. Тогда высота подъема:
3. Ответ: 1,2 м

Задача 4. В широкой части горизонтально расположенной трубы нефть течет со скоростью м/с. Определить скорость течения нефти в узкой части трубы, если разность давлений в широкой и узкой частях трубы составляет мм рт. ст.

• Здесь нам снова придет на помощь уравнение Бернулли, из него можно исключить слагаемые, в которые входит высота подъема, так как по условию труба расположена горизонтально. Тогда уравнение примет вид:
• Разность скоростей:
• Прежде чем подставлять числа, надо выразить давление в Паскалях:
• Ответ: 4,16 м/c

Источник: https://easy-physic.ru/uravnenie-bernulli-teorema-o-nerazry-vnosti-strui/

Уравнение неразрывности потока

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. расходы во входном и выходном сечениях напорной трубы равны:

q1 = q2.

Если отсюда выразим скорость для выходного сечения

то заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Гидродинамический напор

Гидродинамический напор H (м) — это энергетическая характеристика движущейся жидкости. Понятие гидродинамического напора в гидравлике имеет фундаментальное значение.

• Гидродинамический напор H определяется по формуле:
• 
• где z — геометрический напор (высота), м;
• hp — пьезометрический напор (высота), м;
• hV = V 2/(2g) — скоростной напор, м;
• V — скорость потока, м/c;
• g — ускорение свободного падения, м2/с.
• 

Гидродинамический напор, в отличие от гидростатического, складывается из трёх составляющих. Дополнительная величина hV отражает кинетическую энергию — движение жидкости. Остальные члены — потенциальную энергию.

Отсчитывают напор от нулевой горизонтальной плоскости 0-0 в метрах по высоте. Величина скоростного напора hV может быть рассчитана по V, или же измерена с помощью пьезометра и трубки Питo по разности уровней жидкости (см.

рис. 11). Трубка Пито — прибор для измерения полного напора текущей жидкости.У трубки Питo, в отличие от пьезометра, нижняя часть, погружённая в жидкость, обращена против движения потока и откликается не только на давление, но и на скорость.

Уравнение Бернулли для идеальной жидкости

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.4.5).

Рис.4.5. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.4.5).

1. Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
2. Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
3. Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
4. Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
5. и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
6. С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
7. z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
8. — удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
9. — удельные кинетические энергии в тех же сечениях.
10. Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.4.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Источник: https://cyberpedia.su/8x112e0.html

Уравнение неразрывности и уравнение Бернулли

Содержание

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости.

Живое сечение может быть ограничено твердыми стенками полностью или частично.

Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным.

Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью.

Эту воображаемую фиктивную скорость называют средней скоростью потока υср .

• Таким образом уравнение расхода для потока будет
• Q = υср * F,
• где Q – расход;
• υср – средняя скорость потока
• F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

1. Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный
2. Q1 = υ1 * F1,
3. а через сечение 2-2 из него же вытекает объем, равный
4. Q2 = υ2 * F2.

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

• Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.
• Таким образом
• Q1 = Q2
• Или
• υ1 * F1 = υ2 * F2
• Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
• Q = υ * F = const.
• Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что
• υ1 / υ2 = F2 / F1

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

1. Если всё это записать в виде формулы, то
2. ΔW = ΣA,
3. где W – приращение кинетической энергии = m * υ2 / 2
4. ΣA – сумма работ действующих сил = P *ΔS
5. В этих выражениях m – масса υ – скорость материальной точки P – равнодействующая всех сил, приложенных к точке,
6. ΔS – проекция перемещения точки на направление силы.

• Теперь рассмотрим обе части этого выражения по порядку.
• Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

1. Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.
2. Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен
3. q * ΔТ
4. масса в этом случае получается равной
5. m = ρ * q * ΔТ
6. Подставляя все это в выражение для кинетической энергии получаем цепочку
7. ΔW = m * υ22 / 2 — m * υ21 / 2 = ρ * q * ΔТ * υ22 / 2 — ρ * q * ΔТ * υ21 / 2
8. Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести AТ равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

• Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.
• AТ = m*g* Z1 — m*g* Z2
• Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления АД , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

1. Суммарно работа сил давления будет
2. АД = (P1*m/ ρ ) — (P2*m/ ρ )
3. Подставляя в начальное уравнение
4. ΔW = ΣA,
5. Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как: Удельная энергия положения = qz Удельная энергия давления = p/ ρ

Кинетическая удельная энергия = υ2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Источник: https://www.nektonnasos.ru/article/gidravlika/uravnenie-nerazryvnosti/

Закон Бернулли в аэродинамике

Подробности Категория: Человек и небо Опубликовано 23.07.2014 16:59 Просмотров: 20237

Какое отношение к авиации имеет закон Бернулли? Оказывается, самое прямое. С его помощью можно объяснить возникновение подъёмной силы крыла самолёта и других аэродинамических сил.

Закон Бернулли

Автор этого закона — швейцарский физик-универсал, механик и математик. Даниил Бернулли — сын известного швейцарского математика Иоганна Бернулли. В 1838 г. он опубликовал фундаментальный научный труд «Гидродинамика», в котором и вывел свой знаменитый закон.

Следует сказать, что в те времена аэродинамика как наука ещё не существовала. А закон Бернулли описывал зависимость скорости потока идеальной жидкости от давления. Но в начале ХХ века начала зарождаться авиация. И вот тут закон Бернулли оказался очень кстати.

Ведь если рассматривать воздушный поток как несжимаемую жидкость, то этот закон справедлив и для воздушных потоков. С его помощью смогли понять, как поднять в воздух летательный аппарат тяжелее воздуха.

Это важнейший законом аэродинамики, так как он устанавливает связь между скоростью движения воздуха и действующим в нём давлением, что помогает делать расчёты сил, действующих на летательный аппарат.

Закон Бернулли — это следствие закона сохранения энергии для стационарного потока идеальной и несжимаемой жидкости.

Чтобы понять сущность закона Бернулли, познакомимся с уравнением неразрывности струи.

Уравнение неразрывности струи

 

Если жидкость течёт по трубе, имеющей разное поперечное сечение, то давление в разных местах трубы будет неодинаковое.

Мысленно выделим в трубе несколько сечений, обозначив их площади S1 и S2. Соответственно, v1 и v2 – скорости течений несжимаемой жидкости через эти сечения.

• За время ∆t через сечения протекут жидкости, объёмы которых будут равны:
• ∆V1 = l1 · S1 = v1 · ∆t · S1;
• ∆V2 = l2 · S2 = v2 · ∆t · S2;

Так как мы рассматриваем стационарное течение несжимаемой жидкости, то по закону сохранения массы через любое поперечное сечение трубы за одинаковый промежуток времени проходит одинаковый объём жидкости. Следовательно, ∆V1 = ∆V2.

1. v1 · ∆t · S1 = v2 · ∆t · S2;
2. то есть, v1 · S1 = v2 · S2;
3. или v1·∆S = const.

Произведение площади поперечного сечения потока на его скорость есть величина постоянная. Это уравнение называют уравнением неразрывности струи.

Уравнение Бернулли

Объединив условие неразрывности жидкости и закон сохранения энергии, Бернулли вывел уравнение, согласно которому с увеличение скорости потока уменьшается давление, и наоборот.

Из уравнения неразрывности следует, что v1/ v2 = S2/ S1

То есть, скорости жидкостей обратно пропорциональны площадям сечений. И чем больше площадь сечения, тем меньше скорость жидкости, протекающей через него, и наоборот.

Подобное явление мы видим, когда стоим на берегу реки и наблюдаем за её течением. В узком месте русла скорость течения воды всегда больше, чем в широком.

Жидкость, поступающая из широкой в более узкую часть трубы, ускоряется. Это означает, что на неё действует сила со стороны жидкости, находящейся в более широкой части трубы.

Откуда же берётся эта сила? Для горизонтальной трубы причина возникновения этой силы — разность давлений в широком и узком участках трубы. В широкой части давление выше, чем в узкой, а скорость ниже.

Отсюда следует вывод: «При стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот».

• Уравнение Бернулли имеет вид:
• , 
• где ρ – плотность жидкости,
• ν – скорость потока,
• h – высота, на которой располагается элемент жидкости,
• ɡ — ускорение свободного падения,
• p – давление в точке пространства, в которой расположен центр массы элемента жидкости.

Первое слагаемое уравнения Бернулли – кинетическая энергия потока, или динамическое давление. Его создаёт движение жидкости или газа. В авиации его также называют скоростным напором.

Второе слагаемое — потенциальная энергия, или гидростатическое давление. Оно создаётся весом столба жидкости или газа высотой h.

1. И, наконец, третье слагаемое, Р – это статистическое давление, которое оказывают друг на друга соседние слои жидкости или газа.
2. Сумма всех слагаемых уравнения называется полным давлением.
3. Для трубы, расположенной горизонтально, или горизонтального воздушного потока уравнение Бернулли выглядит так:
4.  
5. Из него видно, что чем выше скорость течения жидкости (а в аэродинамике – скорость воздушного потока), тем меньше давление, и наоборот.

Эффект Бернулли можно наблюдать, сидя у камина. Во время сильных порывов ветра скорость воздушного потока возрастает, а давление падает. В комнате давление воздуха выше. И языки пламени устремляются вверх в дымоход.

• Закон Бернулли и авиация
•  
• С помощью этого закона очень просто объяснить, как возникает подъёмная сила для летательного аппарата тяжелее воздуха.

Во время полёта крыло самолёта как бы разрезает воздушный поток на две части. Одна часть обтекает верхнюю поверхность крыла, а другая нижнюю.

Форма крыла такова, что верхний поток должен преодолеть больший путь для того, чтобы соединиться с нижним в одной точке. Значит, он двигается с большей скоростью.

А раз скорость больше, то и давление над верхней поверхностью крыла меньше, чем под нижней. За счёт разности этих давлений и возникает подъёмная сила крыла.

Сразу сделаем уточнение, что вышеописанные законы действуют, если скорость движения воздушного потока не превышает скорость звука (до 340 м/с). Ведь мы рассматривали воздух как несжимаемую жидкость. Но оказывается, что при скоростях выше скорости звука воздушный поток ведёт себя по-другому. Сжимаемостью воздуха пренебрегать уже нельзя.

И воздух в этих условиях, как любой газ, старается расшириться и занять больший объём. Появляются значительные перепады давления или ударные волны. А сам воздушный поток не сужается, а, наоборот, расширяется.

Решением задач о движении воздушных потоков со скоростями, близкими или превышающими скорость звука, занимается газовая динамика, возникшая как продолжение аэродинамики.

Используя аэродинамические законы, теоретическая аэродинамика позволяет сделать расчёты аэродинамических сил, действующих на летательный аппарат. А правильность этих расчётов проверяют, испытывая построенную модель на специальных экспериментальных установках, которые называются аэродинамическими трубами. Эти установки позволяют измерить величину сил специальными приборами.

Кроме исследования сил, действующих на аэродинамические модели, с помощью аэродинамических измерений изучают распределение значений скорости, плотности и температуры воздуха, обтекающего модель.

Источник: http://ency.info/materiya-i-dvigenie/chelovek-i-nebo/312-zakon-bernulli

Уравнение неразрывности потока. Вывод уравнения. Применение уравнения к решению практических задач

Основным условием, которое должно соблюдаться при течении жидкости, является непрерывность изменения параметров потока в зависимости от координат и времени, т.е. при течении жидкости должны быть соблюдены условия при, которых жидкость должна двигаться в канале как сплошная среда, без разрывов.

Выделим внутри пространства с движущейся капельной жидкостью неподвижный контур в форме элементарного параллелепипеда с ребрами dx, dy, dz(см. рис. 2.35).

Обозначим скорость жидкости, которая втекает в левую грань параллелепипеда, через . Скорость жидкости, вытекающей из правой грани, вследствие неразрывности поля скоростей равна

Рис. 2.35. Движение жидкости через контур

Поскольку рассматриваемый элементарный объем неподвижен, изменение скорости не зависит от времени. В направлении оси х через левую грань втечет за 1 с жидкость массой , а вытекает через правую грань

Значит, за 1 с из параллелепипеда вытекает в направление оси х жидкости больше, чем втекает, на

Аналогичные выражения получаются и для направлений x, y, z. Закон сохранения массы требует, чтобы сумма трех полученных приращений была равна нулю:

.

(2.33)

Это уравнение называют уравнением неразрывности, т.к. оно предполагает, что жидкость является сплошной средой.

Рассмотрим уравнение неразрывности для случая течения струйки при установившемся движении. Масса жидкости течет в трубке тока (см. рис. 2.34). Пусть левое входное сечение трубки тока имеет площадь и в этом сечении скорость жидкости , а ее плотность . Площадь сечения на выходе из трубки тока , скорость течения жидкости , и ее плотность . Скорости струйки направлены по касательной к стенкам трубки тока, поэтому через стенки обмен массой с окружающей жидкостью отсутствует. Через левое сечение втекает в единицу времени масса жидкости . Через правое сечение вытекает в единицу времени масса жидкости . В трубке тока масса жидкости, находящаяся между левым и правым сечениями, остается постоянной, следовательно, условие сплошности потока в трубке тока будет:

const.

(2.34)

Если плотность жидкости по длине трубки тока не изменяется, т.е. = , то можно записать для левого и правого сечений:

= const или const.

(2.35)

Полученное уравнение является уравнением неразрывности для трубки тока.

Для потока реальной жидкости уравнение неразрывности записывается в следующем виде:

,

(2.36)

• где и – площади сечения потока в сечениях на входе и на выходе; и – средние скорости потока в этих сечениях.
• Можно сделать два важных вывода:
• 1. При установившемся движении жидкости объемный расход не меняется;

2. При увеличении площади сечения потока жидкости средняя скорость уменьшается, и, наоборот, при уменьшении сечения — скорость увеличивается.

14. Уравнение Д.Бернулли для элементарной струйки идеальной жидкости.

Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и2-2.Площади живых сечений потока обозначим dЙ1 и dЙ2.

Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0- 0 характеризуется величинами z1и z2.

Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

За малый промежуток времени dt частицы жидкости из 1-1 переместятся в 1'-1' на расстояние, равноеu1dt, а частицы из 2-2 в 2' — 2' на расстояние u2dt.

Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести.

Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки.

Она будет равна произведению силы p1dЙ1 на путь u1dt:

.

Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

1. .
2. Полная работа, выполненная силами давления, примет вид:
3. .
4. Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:
5. .
6. При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (z1 – z2) и работа, произведённая силами тяжести, составит:
7. .
8. Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.
9. Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит
10. .
11. Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду:
12. .

Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим

• .
• После сокращения и преобразований придём к искомому виду

Если учесть, что сечения 1-1 и 2-2 выбраны произвольно, можно прийти к выводу, что сумма приведённых выше величин описывающих движение жидкости под действием сил давления и сил тяжести есть величина постоянная для элементарной струйки, т.е.

Таким образом, снова получено то же (ранее полученное интегрированием уравнений Эйлера) уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении под действием сил тяжести.



Источник: https://infopedia.su/3x58c9.html

Гидравлические элементы потока, расход, средняя скорость. Уравнение неразрывности (сплошности) потока

В качестве основных элементов, характеризующих поток жидкости, различают: площадь живого сечения, смоченный периметр, гидравлический радиус, эквивалентный диаметр, средняя скорость потока, расход жидкости.

Живым сечением называется сечение потока, проведенное перпендикулярно линиям тока. (Линией тока называется такая линия, касательные к которой в любой точке, совпадают с направлением векторов скорости частиц в данный момент времени.)

Смоченный периметр – часть периметра живого сечения потока, в которой жидкость соприкасается с твердыми стенками канала или трубы. (χ, м).

Гидравлический радиус – характеристика живого сечения, представляющая собой отношение площади живого сечения к смоченному периметру

Средняя скорость – фиктивная скорость (v, м/с), с которой должны двигаться все частицы жидкости в данном живом сечении, чтобы расход, проходящий через него, был равен расходу, вычисленному по действительным скоростям всех частиц в этом же сечении. v=Q/w

Расход– количество жидкости, протекающей через живое сечение потока в единицу времени.

расход жидкости по тока равен произведению площади его живого сечения на среднюю скорость(Q=v * w). При движении жидкости различают, соответственно расходы: объемный, весовой и массовый.

u1 w1=u2 w2=……=un wn=const

Это уравнение называется уравнением неразрывности (сплошности) для элементарной

струйки. Оно показывает, что при установившемся движении элементарный объемный расход несжимаемой жидкости есть величина постоянная вдоль всей струйки.

Учитывая, что поток жидкости представляет собой совокупность большого числа элементарных струек, сплошь заполняющих площадь его живого cечения, общий расход жидкости для всего потока, очевидно, можно определить как сумму

элементарных расходов отдельных струек, из которых состоит

поток, т.е.

Q = Ʃu*w

u – скорость элементарных струек

Уравнение Д. Бернулли для элементарной струйки невязкой жидкости.

z+р/γ+u2/2g=const

Это и есть уравнение Д. Бернулли для элементарной струйки идеальной жидкости. Оно показывает, что для элементарной струйки идеальной жидкости полная удельная энергия, т .е . сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии,есть величина постоянная во всех сечениях.

Члены уравнения Бернулли измеряются в единицах длины и носят следующие название: z — нивелирная высота, или геометрический напор; р/γ — пьезометрическая высота; u2/2g —

скоростная высота, или скоростной напор.

Уравнение Д. Бернулли для элементарной струйки реальной жидкости. Геометрическое и энергетическое толкование уравнения Д. Бернулли.

Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеивание (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Для реальной жидкости равенство нарушается, и вместо него имеем , где – потеря напора на участке 1–2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид

Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне

Например, на участке трубопровода 1–2 (см. рис. 4.26)

• где l1-2 – длина участка 1–2.
• Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит.
• Кроме того, вводится еще понятие о пьезометрическом уклоне

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник: https://zdamsam.ru/a23835.html

ФизМат

Гидродинамика и аэродинамика.

Гидродина́мика 
и аэродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.

Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Характеристики течения.

Течение — движение жидкости

Поток жидкости (газа) и уравнение неразрывности.

Поток — совокупность частиц движущейся жидкости. Уравнения неразрывности для несжимаемой жидкости: произведение скорости течения несжимаемой жидкости на поперечной сечение трубки тока есть величина постоянная для данной трубки тока. S1v1 = S2v2 или Sv=const. где S-площадь поперечного сечения

Уравнение Бернулли для жидкости (газа).

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

 p— плотность жидкости,
 v— скорость потока,
 h— высота, на которой находится рассматриваемый элемент жидкости,
 p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
 g— ускорение свободного падения.

Гидравлический пресс.

Гидравлический пресс — это простейшая гидравлическая машина , предназначенная для создания больших сжимающих усилий.

Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью, водой, маслом или другой подходящей жидкостью.

По законам французского философа и учёного Паскаля, давление (то есть сила, действующая на единицу площади) в любом месте жидкости (или газа), находящейся в покое, одинаково по всем направлениям и одинаково передается по всему объёму.

 Закон Паскаля — самый главный закон гидростатики. Все заводы гидравлических прессов при их производстве основываются на законе гидростатики.

По сути гидравлический пресс можно сравнить с эффектом рычага, где в качестве передающего усилие объекта используется жидкость, а усилие зависит от величины отношения площадей рабочих поверхностей. но это не обязательно

Источник: http://fizmatinf.blogspot.com/2012/12/19_23.html