Теорема о трех перпендикулярах и обратная теорема

Содержание

Работа предназначена для учащихся общеобразовательных классов. Презентация может быть использована при знакомстве с темой: «Теорема о трёх перпендикулярах и обратная ей теорема».

Формулировка теоремы записана на математическом языке, чтобы учащиеся могли самостоятельно сформулировать теорему, обратную теореме о трёх перпендикулярах. Доказательство теоремы записано с пропусками ( как в ТПО), чтобы учащиеся могли сначала самостоятельно провести доказательство с дальнейшей проверкой с помощью слайдов презентации.

Далее показано применение этой теоремы при решении задач, взятых из сборника Рабиновича Е.М. «Задачи и упражнения на готовых чертежах. 10-11 класс».

Учебник: Атанасян Л.С. Геометрия 10-11кл.

Учитель : Гусева Н.П .

перпендикуляр
A
наклонная

H
основание перпендикуляра
C
основание наклонной
проекция наклонной
на плоскость 

____  AC наклонная CH m Док-во : 1. По условию AH   = по опр. АН  ___, АН  ___ 2. Рассмотрим плоскость (А HC ). Прямая m  (А HC ) (по ___________________________ ), т.к. m  ___ , m  ___ . 3. По ____________________ m перпендикулярна любой прямой, лежащей в плоскости ______ . А значит, m  ___. CH m А AH CH признаку перпендикулярности определению AH С A С Н m С » width=»640″

Прямая, проведенная в плоскости через основание наклонной _______________ к ее проекции на эту плоскость, перпендикулярна и к _____________________.
перпендикулярна
самой наклонной
перпендикуляр
Рассмотрим отрезок AH — _______________ к плоскости  , АС — __________, m – прямая, проведенная в плоскости  через точку С.
m  _____ = ____  AC
наклонная
CH
m
Док-во :

1. По условию AH   = по опр. АН  ___, АН  ___

2. Рассмотрим плоскость (А HC ). Прямая m  (А HC )

(по ___________________________ ), т.к. m  ___ , m  ___ .

3. По ____________________ m перпендикулярна любой прямой, лежащей в плоскости ______ . А значит, m  ___.

CH
m
А
AH
CH
признаку перпендикулярности
определению
AH С
A С
Н
m
С


____  НС наклонная AC m Док-во : 1. По условию AH   = по опр. АН  ___, АН  __ _ 2. Рассмотрим плоскость (А HC ). Прямая m  (А HC ) (по _____________________________ ), т.к. m  ___ , m  ___ . 3. По ___ _____________ ____ m перпендикулярна любой прямой, лежащей в плоскости ______ . А значит, m  ___. m HC А АС А H признаку перпендикулярности определению AHC HC Н m С » width=»640″

Прямая, проведенная в плоскости через основание наклонной _______________ к ней, перпендикулярна и к ее___ ________ ____.
перпендикулярно
проекции
перпендикуляр
Рассмотрим отрезок AH — _______________ к плоскости  , АС — __________, m – прямая, проведенная в плоскости  через точку С.
m  _____ = ____  НС
наклонная
AC
m
Док-во :

1. По условию AH   = по опр. АН  ___, АН  __ _

2. Рассмотрим плоскость (А HC ). Прямая m  (А HC )

(по _____________________________ ), т.к. m  ___ , m  ___ .

3. По ___ _____________ ____ m перпендикулярна любой прямой, лежащей в плоскости ______ . А значит, m  ___.

m
HC
А
АС
А H
признаку перпендикулярности
определению
AHC
HC
Н
m
С


3. Построить перпендикуляр из точки M к прямой BC.

Доп. постр. AH  BC

 CAH = 30 
A
B
BC=AC= 2CH
30 
120 
BC :CH=2:1
C
H
a

М O  OH Доп. постр. OH  BC По теореме о трех перпендикулярах MH  BC M 12 А 1 5 O OH – средняя линия  АВС OH = AC/2 B 9 1 8 OH=9 H 1 0 В  MOH – прямоугольном MH = 144+81=15 C a» width=»640″

4 . Найти расстояние от точки M до прямой В C.

М O  (ABC) = М O  OH

Доп. постр. OH  BC

По теореме о трех перпендикулярах
MH  BC
M
12
А
1 5
O
OH – средняя линия  АВС
OH = AC/2
B
9
1 8
OH=9
H
1 0
В  MOH – прямоугольном
MH = 144+81=15
C
a

6. ABCD — параллелограмм . Найти расстояние от точки М до прямой AD .

Доп. постр. BH  AD

По теореме о трех перпендикулярах
MH  AD
M
8
 A =  C = 30 
10
C
B
BH = AB/2
BH = 6
30 
12
6
30 
А
В  MHB – прямоугольном
MH = 64 + 36 =10
H
D
a

по признаку C 1 C  (BCD) D 1 A 1 По теореме о трёх перпендикулярах C 1 D  AD Поэтому  ( C 1 , AD ) = C 1 D С B В  C 1 CD – прямоугольном C 1 D = 4 + 4 =2 2 D A» width=»640″

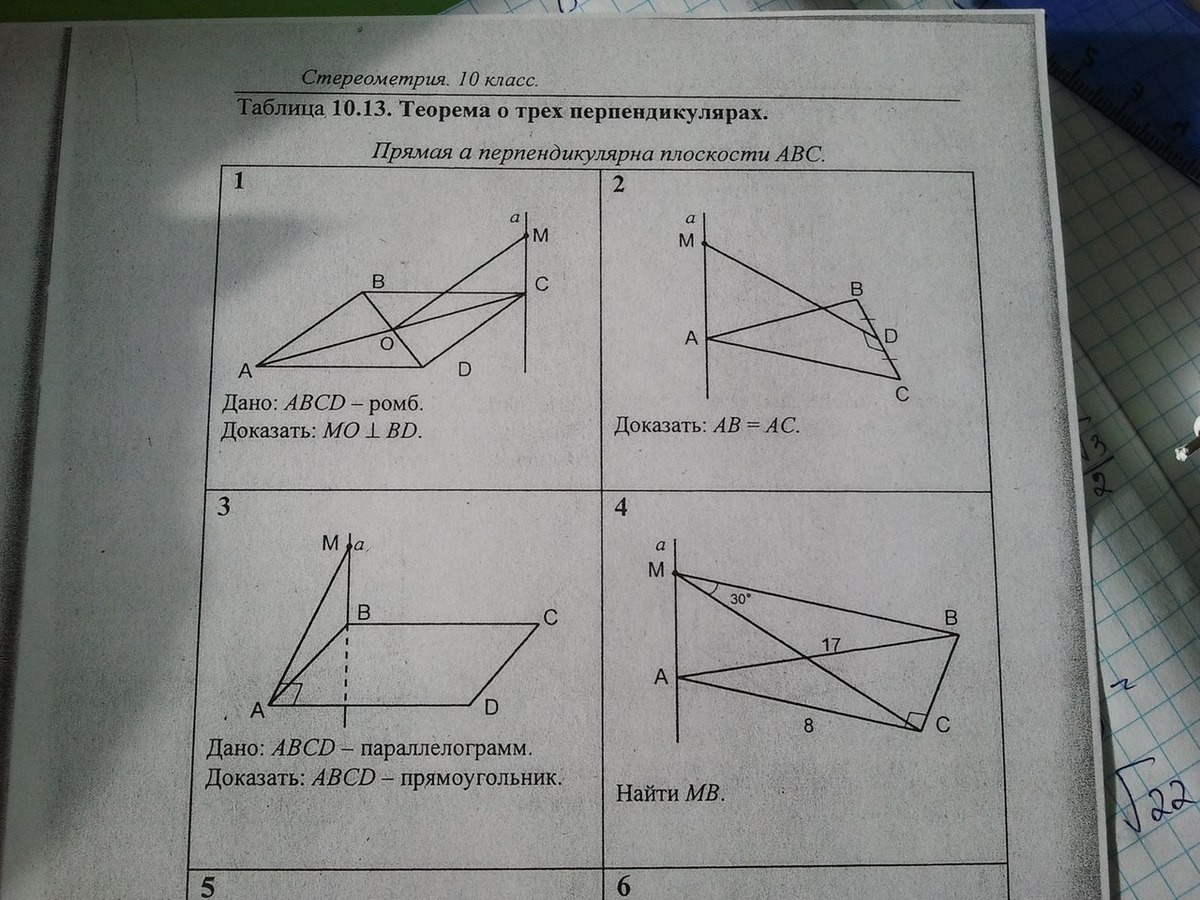
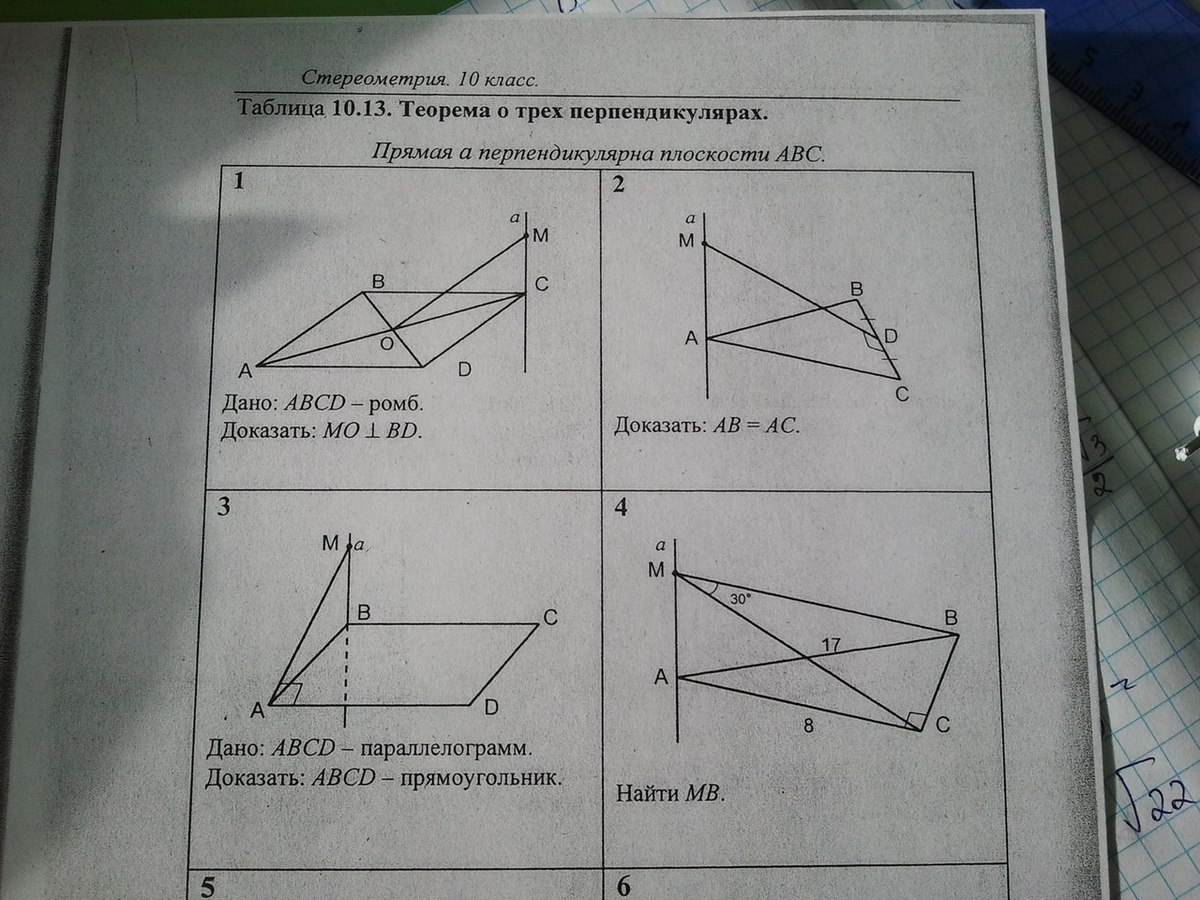
7. На рисунке А BCDA 1 B 1 C 1 D 1 – куб, ребро которого равно 2. Найти расстояние от вершины С 1 до прямой, содержащей ребро AD.

B 1
С 1
C 1 C  BC, C 1 C  CD =
по признаку C 1 C  (BCD)
D 1
A 1
По теореме о трёх
перпендикулярах C 1 D  AD
Поэтому  ( C 1 , AD ) = C 1 D
С
B
В  C 1 CD – прямоугольном
C 1 D = 4 + 4 =2 2
D
A

2см
9 см
6см
7см
№ 150 ( a )
По теореме о трёх
перпендикулярах KD  DC
K
В  KDC – прямоугольном
DC = 81 — 36 = 3 5см
B
C
 ( K , (ABC) ) = KA
3 5см
В  KAB – прямоугольном
KA = 49 — 45 = 2 см
A
D
AK  (ABC)

ДОМАШНЕЕ ЗАДАНИЕ
№ 152, 154, 155
_______________________________________________________
Для тех, кто справился
со всеми задачами на уроке :
№ 157, 158, 159
УДАЧИ!

Источник: https://kopilkaurokov.ru/matematika/presentacii/tieoriema-o-triokh-pierpiendikuliarakh-i-ieio-primienieniie-pri-rieshienii-zadach

Теорема о трех перпендикулярах — правило, формулировка и примеры решения задач

Одним из важных утверждений стереометрии (так называется геометрия в пространстве) является теорема о трёх перпендикулярах.

Она помогает при нахождении прямых углов, сведении задачи к применению теоремы Пифагора и тригонометрических функций, что в целом значительно упрощает вычислительную работу.

Формулировка теоремы о трёх перпендикулярах

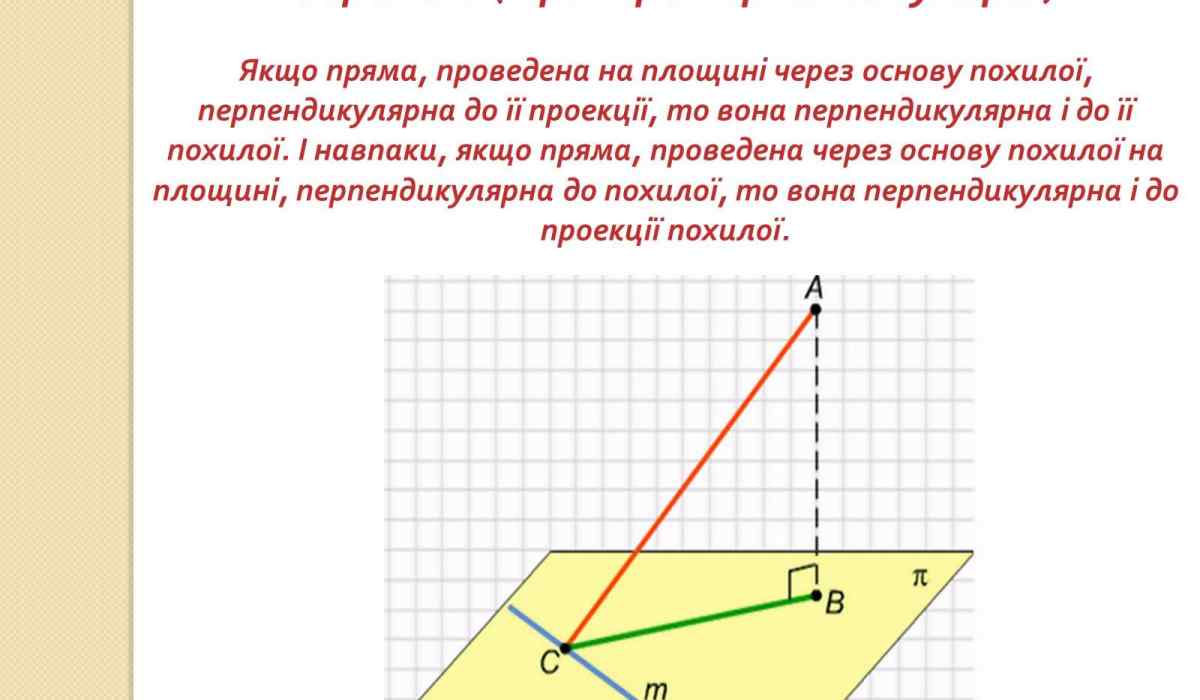
Прямая, проведённая на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и к самой наклонной.

Доказательство теоремы

Существуют принципиально различные методы.

Первый метод

Основан на равенстве наклонных при равных проекциях.
Проведя к плоскости α отрезок AB, AB ⊥ α, B ∈ α через точку A_AC, C ∈ α, b ⊥ BC, C ∈ b, b ⊂ α, возникает необходимость убедиться, что b ⊥ AC.

От C на прямой b откладывают равные отрезки CD, CE, затем соединяют точки D; E с B, A.

Поскольку CD, CE равны по построению, b ⊥ BC, BC — общий катет, то треугольники ΔBCD, ΔBCE, являющиеся прямоугольными, равны. Следовательно, BD = BE.

Из полученного условия вытекает равенство наклонных AD, AE (lkz rjnjhs[ BD, BE – проекции). Поэтому ΔAED является равнобедренным.

По построению CD = CE, откуда следует искомая перпендикулярность прямых AC и b.

Доказано.

Второй метод

Основан на определении, свойствах, признаках перпендикулярности прямой и плоскости.

AB и b – скрещивающиеся. BC – их общий перпендикуляр, AC – наклонная к α.

Проводя FC параллельно AB, получают FC ⊥ α.

Так как по условию b ⊥ AC, по построению b ⊥ FC, то b ⊥ ACF.
Из того, что C ∈ ACF, A ∈ ACF, следует, что AC ⊂ ACF, отсюда b ⊥ AC.
Доказано.

Теорема, обратная теореме о трёх перпендикулярах

Меняя местами понятия проекции и наклонной, получают взаимно обратное утверждение:
Если прямая, проведённая в плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

Доказательства аналогичны уже приведённым ранее.

Решение задач на применение теоремы

Класс заданий, связанных с использованием рассматриваемого материала, довольно обширен. Многие стереометрические задачи сводятся к поиску прямых углов в исследуемом объекте, после чего вопрос о существовании и нахождении неизвестных компонент переходит в область несложных вычислений.

О единственности подхода говорить не приходится, поскольку любые формулы, правила, свойства могут быть получены, исходя из различных базовых данных и условий.

Задача №1

Доказать, что каждая точка прямой, перпендикулярной плоскости треугольника и проходящей через центр вписанной окружности, равноудалена от его сторон.

Решение.
Условие со всеми дополнительными построениями изображено на рисунке.
В силу касания окружностью сторон, каждый из радиусов OA, OB, OC образует угол в 90º. Отрезки SA, SB, SC составляют со сторонами прямые углы, а их длины являются искомыми расстояниями
от точки S.
ΔAOS = ΔBOS = ΔCOS по двум катетам (SO – общий, OA = OB = OC = r), следовательно, SA = SB = SC.
Доказано.

Задача №2

Основанием пирамиды MABCD служит прямоугольник со сторонами 6 и 8. Высота MB равна 2. МВ перпендикулярна плоскости прямоугольника АВСD.

Найти расстояние от точки M до диагонали CA и длину ребра MD.
Решение.

Для ответа на первый вопрос требуется знать определение расстояния. Это длина перпендикуляра, проведённого из данной точки на прямую.

Пусть MH – искомое расстояние. Тогда MH ⊥ AC.

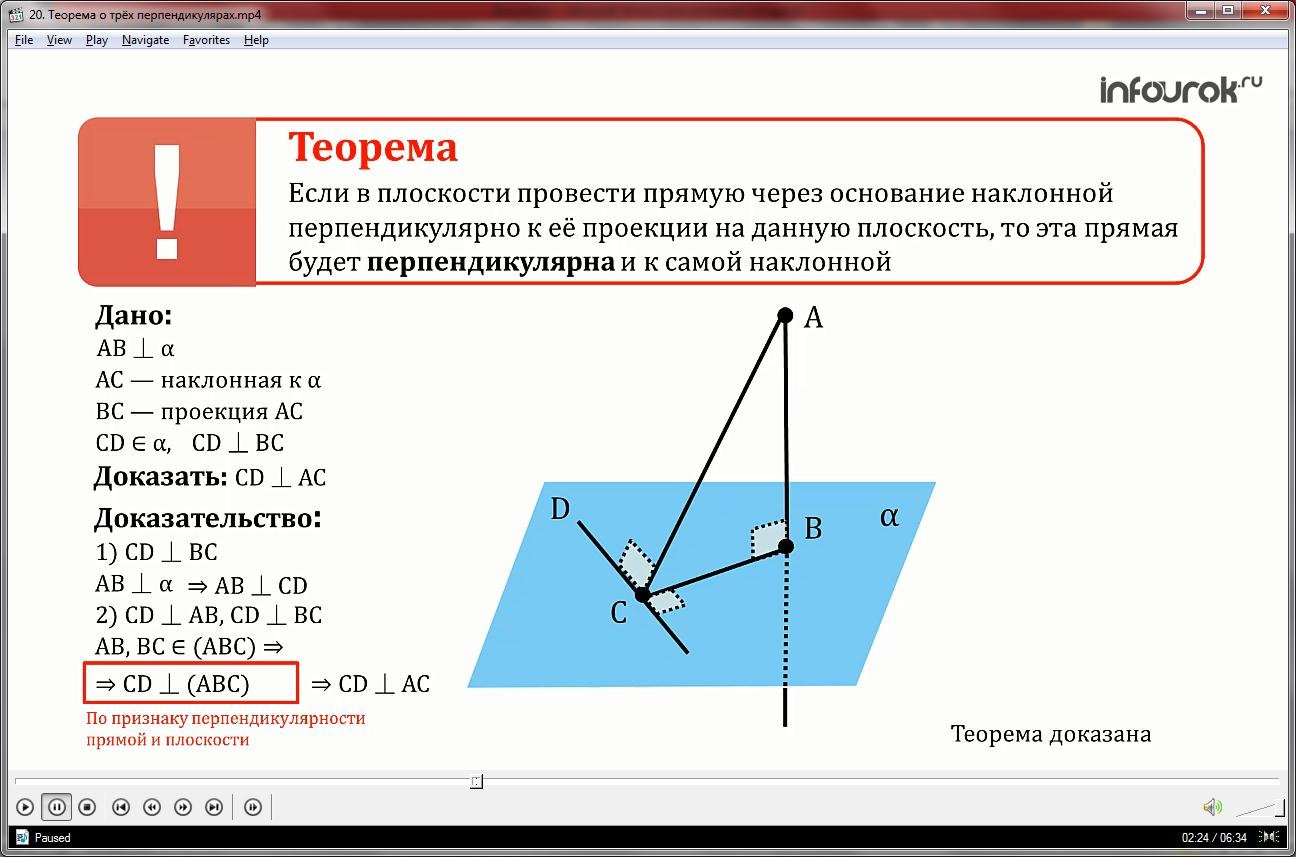
По второму утверждению BH ⊥ AC.
Поскольку ΔABC – прямоугольный, то BH, как высоту, можно вычислить по формуле:

Вычислить AC несложно:

Таким образом,

Отсюда:

Учитывая, что диагонали прямоугольника имеют одинаковые длины, находят MD:

Ответ:

Источник: https://nauka.club/matematika/geometriya/teorema-o-tryekh-perpendikulyarakh.html

Теорема о трех перпендикулярах: доказательство обратной, что такое перпендикулярность, задачи с решением

В этой статье рассмотрена одна из самых важных теорем в стереометрии – теорема о трех перпендикулярах. Важность ее заключается в том, что прежде чем переходить к решению сложных фигур – сфер, пирамид и параллелепипедов, необходимо владеть основными законами, возникающими при взаимодействиях прямых в пространстве….

Базовые понятия

Для понимания сути теоремы нужно владеть базовыми понятиями планиметрии.

Сплошь и рядом в геометрии используется понятие угол. Измеряются они в градусах или радианах. Радианы – незаменимая размерность в тригонометрии, градусы более привычны нам, потому что пришли из реальной жизни.

0 град., 90 град., 180 град. – три типа углов, которые понятны нам не только геометрически, но и интуитивно. 90 град. (или прямой) – самый, вероятно, популярный тип, потому что активно встречается в повседневной жизни.

Перпендикулярностью назовем такое соотношения между фигурами (прямыми, плоскостями и т.д.), при котором угол между ними составляет 90 градусов.

Внимание! Перпендикуляр – это прямая, которая составляет угол 90 град. с другими прямыми или плоскостями.

Изучим терминологию на реальных примерах:

Имеется плоскость α. С – точка, не лежащая на плоскости. СВ – отрезок, опущенный из точки С на плоскость α и составляющий с плоскостью прямой угол. Таким образом СВ ⊥ α. Обозначим наклонную, т.е. луч, выходящий тоже из С. Он пересекает α в точке А. АВС – прямоугольный треугольник, поскольку СВА равен 90 град.

Теорема

Несмотря на всю свою простоту, теорема о трех перпендикулярах связывает между собой углы, находящиеся в различных плоскостях, поэтому данный закон считается довольно глобальным в геометрии.

Картина такая же, как в предыдущем разделе: есть α, точка А, лежащая за пределами α. Из этой точки опущен перпендикуляр, имеющий основание В, также проведен отрезок АС (который является наклонной).

Вот как звучит формулировка теоремы о трех перпендикулярах:

Если через основание проведенной наклонной проходит прямая и она образует угол 90 град. с проекцией, то она образует такой же угол с ее наклонной.

Таким образом, теорема гласит, что, если между с и ВС – прямой угол, то он прямой между с и АС.

Докажем данную теорему:

ВА – отрезок,составляющий с плоскостью α угол 90 град.,
СА – отрезок прямой, являющейся наклонной,
с – проходит через точку С и образует прямой угол с отрезком ВС.

Проводим КС || ВА. Значит, он составляет угол 90 град. по отношению к α. Это означает, что он составляет углы 90 град. со всеми прямыми, находящимися в α. Между КС и с угол 90 градусов, поскольку она тоже принадлежит α.

Любые два отрезка, которые параллельны друг другу, задают плоскость. Поэтому существует плоскость β через отрезки ВА и КС. Прямая с ⊥ СВ и с ⊥ КС, т.е. она составляет угол 90 град. с каждой прямой, принадлежащей β, отрезку СА в том числе.

Нам удалось доказать теорему о трех перпендикулярах.

Обратная теорема о трех перпендикулярах

Приведем точную формулировку обратной теоремы.

Если через основание проведенной наклонной проходит прямая и она составляет с наклонной угол 90 градусов, то она образовывает такой же угол с ее проекцией.
Таким образом, теорема гласит, что, если между с и АС – прямой угол, то он прямой между с и ВС.
Докажем данную теорему:

ВА – отрезок, составляющий с плоскостью α угол 90 град.,
СА – отрезок прямой, являющейся наклонной,
с – проходит через точку С и имеющая прямой угол с отрезком ВС.

Проводим КС || ВА. Значит, он составляет угол 90 градусов по отношению к α. Это означает, что он составляет углы 90 градусов со всеми прямыми, находящимися в α. Между КС и с – угол 90 град., поскольку она тоже принадлежит α.

Любые два отрезка, которые параллельны друг другу, задают плоскость. Поэтому существует плоскость β через отрезки ВА и КС. Прямая с ⊥ СВ и с ⊥ КС, т.е. она составляет угол 90 градусов с каждой прямой, принадлежащей β, отрезку СА в том числе.

Применение теоремы

Мы привели вам доказательство теоремы о трех перпендикулярах и обратной теоремы. Как вы могли убедиться, для доказательства нам понадобились самые простейшие и базовые аксиомы стереометрии. Сама теорема о трех перпендикулярах имеет крайне широкое применение в решении различных задач.

Внимание! Не существует такой математической задачи, которая не имеет аналогий в реальной, повседневной жизни. Когда речь заходит о геометрии, особенно о стереометрии, то это становится заметным еще больше.

Для того чтобы показать вам широту применения доказанной нами теоремы, рассмотрим две интересные задачи с ее применением.

Задача 1

В треугольник вписана окружность. Через центр этой окружности О проведена прямая SO, составляющая с плоскостью треугольника угол 90 градусов. Правильно ли утверждение, что точка S удалена от сторон на одинаковое расстояние?

Решение:

Поскольку радиус окружности ОА составляет со стороной треугольника (как радиус и касательная к окружности) 90 град., то по теореме о трех перпендикулярах SA составляет со стороной треугольника угол 90 град.

Проанализируем SAO. Поскольку SO составляет с плоскостью, в которой расположен треугольник, угол 90 град., то SAO является прямоугольным треугольником, к которому можно применить теорему Пифагора:

где r = АО = ВО = СО радиус окружности.

Рассматривая SOB и SOC и применяя к ним те же самые вычисления, получаем их гипотенузы:

Таким образом, видим, что SA=SB=SС. Это означает, что да, точка S удалена от сторон на одинаковое расстояние.

Задача 2

Есть прямоугольный треугольник АВС. Высота СН равна 9,6. Из угла С (90 град.) к плоскости треугольника проведен отрезок СМ, который образует перпендикулярность с плоскостью. Его длина равна 28. Найдите кратчайшую длину отрезка между М и гипотенузой.

Ознакомимся с решением:

СН является высотой, МН можно рассматривать как наклонную.

Тогда СН является не только высотой треугольника, но и проекцией МН на плоскость треугольника.

Поскольку между СН и АВ угол 90 град., то по рассматриваемой выше теореме МН ⊥ АВ (наклонная прямой). Таким образом, МН и есть кратчайший отрезок между точкой М и АВ.

МСН – прямоугольный треугольник, поскольку МС ⊥ СН. А значит, можно применить теорему Пифагора:

Длина искомого отрезка найдена.

Источник: https://tvercult.ru/nauka/obratnaya-teorema-o-treh-perpendikulyarah

Теорема о трех перпендикулярах

Неопубликованная запись

Как ее использовать в задачах
Как оформлять на ЕГЭ
Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?

Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.

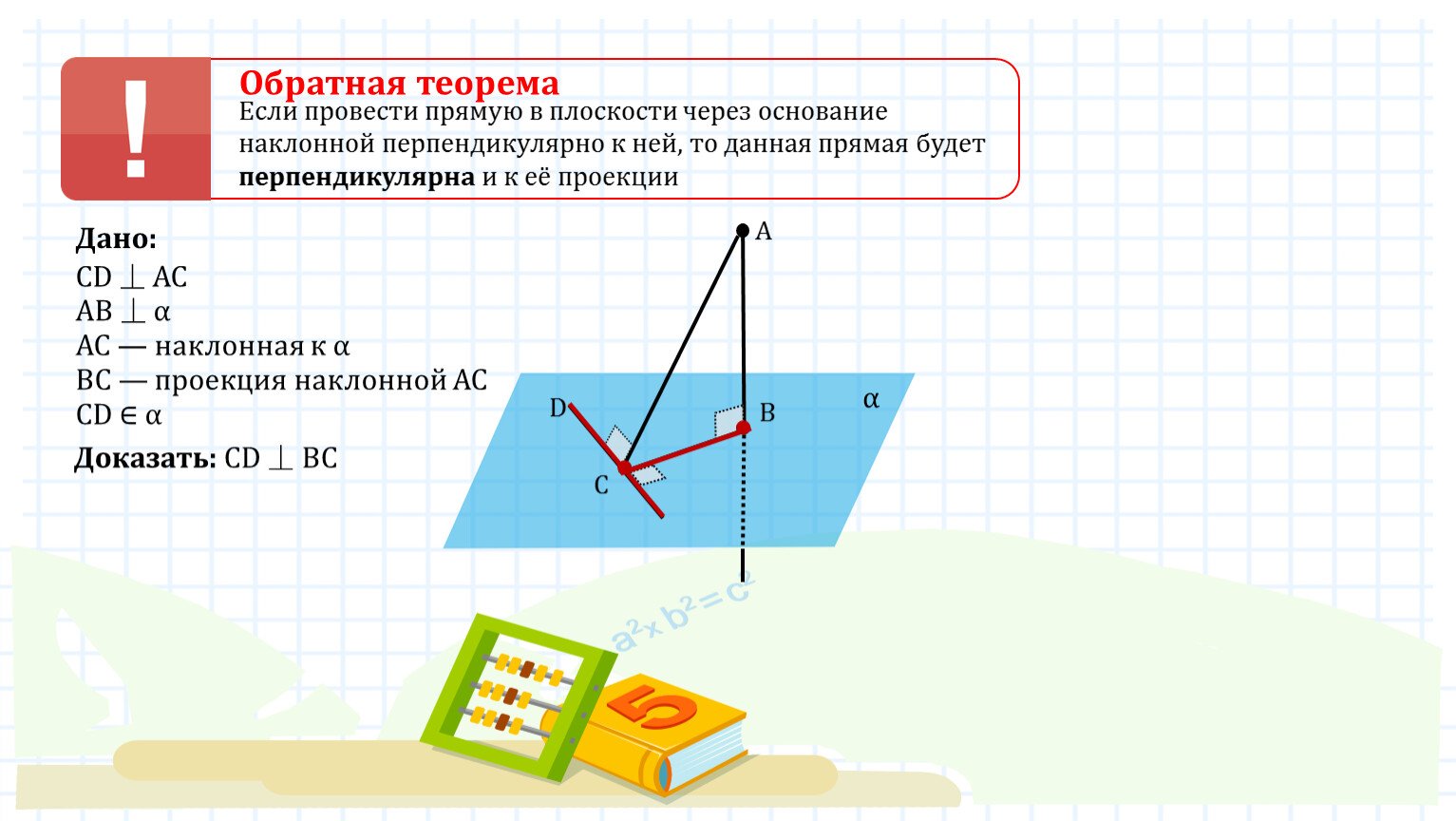
Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).

Перейдем к самому распространенному примеру:

1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны

У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.

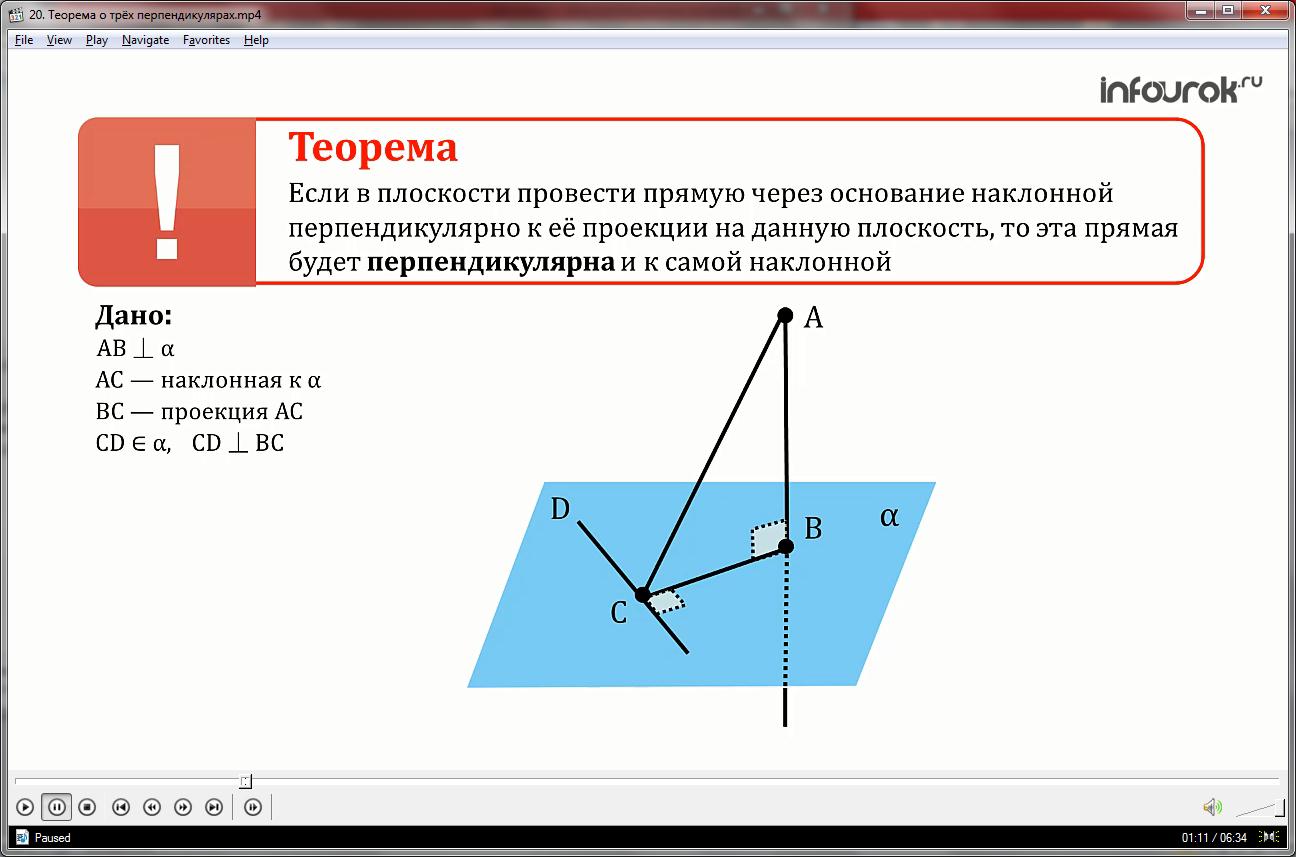
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:

Тогда, чтобы доказать, что AD ⊥ BC: 1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.

2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.
После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).

2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.

Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.

1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).2) BC ⊥ CD т.к. ABCD — прямоугольник.

3) По т.т.п.: B₁C ⊥ CD.

Два пункта доказательства, третий пункт вывод.

3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.

Скажем, что BC — наклонная к плоскости (ABC):

1) SA ⊥ (ABC) => SA ⊥ AC2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).

3) По т.т.п.: SB ⊥ AC.

Вывод:

Два пункта доказательство и вывод!1) Перпендикуляр будет опускаться на плоскость под 90

°.2) Проекция наклонной на плоскость перпендикулярна прямой.

3) По т.т.п. наклонная перпендикулярна прямой.

Источник: https://ik-study.ru/ege_math/tieoriema_o_triekh_pierpiendikuliarakh

Теорема о трех перпендикулярах

Какими способами мы можем доказать перпендикулярность двух прямых?
1.
Используя определение перпендикулярности прямой и плоскости.
Сформулируйте суть способа
Если одна из данных прямых перпендикулярна плоскости, в которой лежит вторая прямая, то данные прямые перпендикулярны
2.
Используя параллельность прямых.
Сформулируйте суть способа
Если есть прямая, которая параллельна одной из данных прямых и перпендикулярна другой, то данные прямые перпендикулярны
2

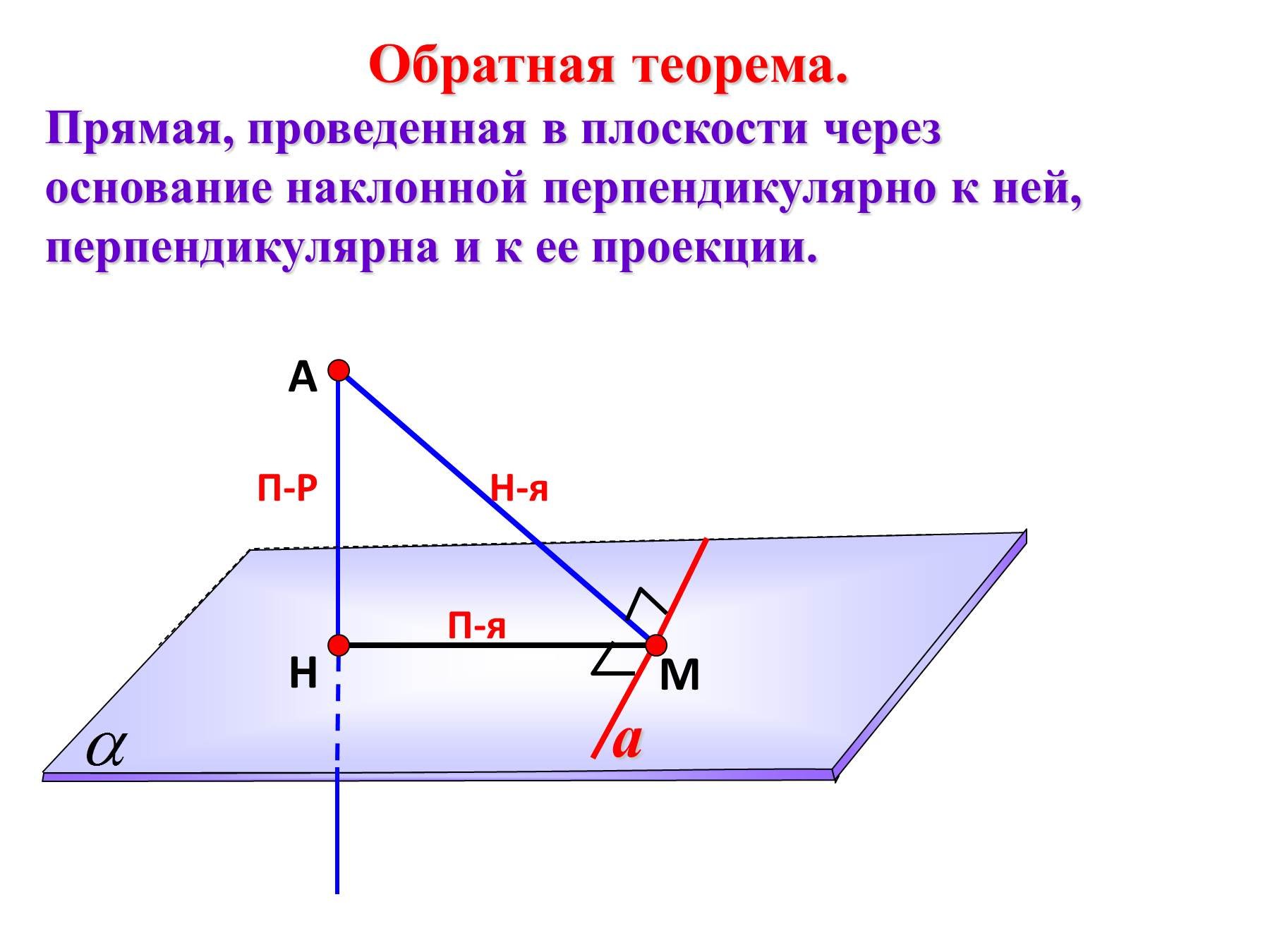
Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно ее проекции на эту плоскость, перпендикулярна и к самой наклонной
еще
О каких фигурах идет речь?
Что о них известно?
Что требуется доказать?
плоскост ь α ,
A
прямая a ,
a  α
?
АМ – наклонная,
M
M є a ,
H
α
a
AH  α
Как построить проекцию наклонной на плоскость?
HM – проекция наклонной,
а  НМ
Изучите рисунок и перечислите 3 перпендикуляра
а  АМ

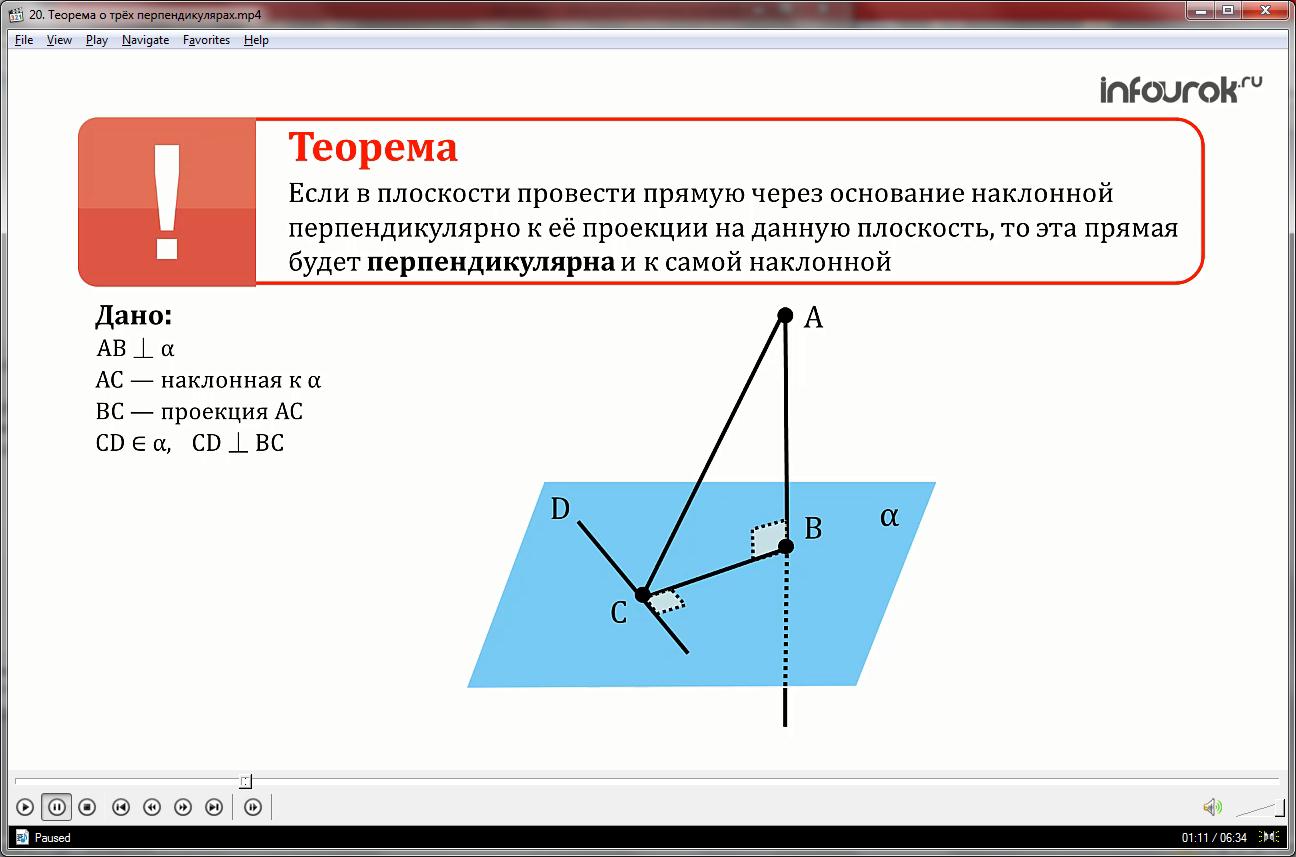
Поиск доказательства.
Дано:
Каким способом доказательства перпендикулярности двух прямых можно воспользоваться?
плоскост ь α ,
a  α
прямая a ,
M є a ,
АМ – наклонная,
AH  α
Используя определение перпендикулярности прямой и плоскости.
HM – проекция наклонной,
а  НМ
?
Доказать:
Какую из данных прямых выберем и перпендикулярность какой плоскости докажем?
а  АМ
A
?
1.
?
Как доказывают перпендикулярность прямой и плоскости?
2.
M
H
Находят в плоскости две пересека-ющиеся прямые, которым данная прямая будет перпендикулярна.
α
a
Каковы эти прямые?
Почему?
НМ  а (по условию)

АН  а , т.к. AH  α

Что требуется доказать?

Составьте план доказательства

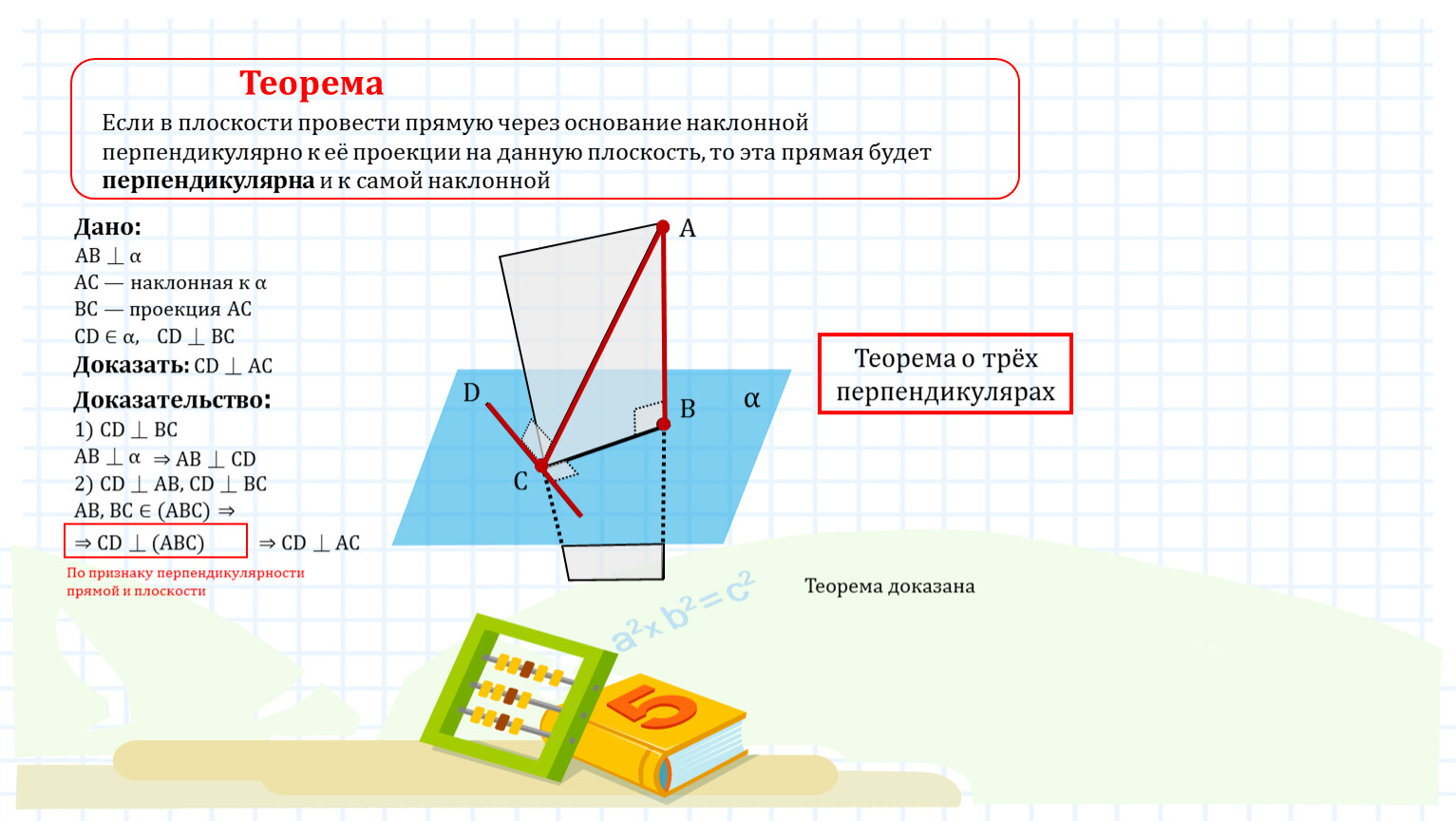
Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Изучите в учебнике доказательство теоремы.
Доказательство:
Рассмотрим плоскость AMH .
Прямая а перпендикулярна к этой плоскости,
так как она перпендикулярна к двум
пересекающимся прямым АН и МН
(а перпендикулярна НМ по условию и
а перпендикулярна АН, так как
АН перпендикулярна плоскости).
Отсюда следует, что прямая а
перпендикулярна к любой прямой,
лежащей в плоскости АМН, в частности, а
перпендикулярна АМ.
Теорема доказана.
1.
2.
,
A
A
A
M
M
M
H
H
H
α
a
a
Выделите этапы доказательства
Какой способ используется для доказательства перпендикулярности прямых?
На чем основано доказательство перпендикулярности прямой и плоскости?

Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Оформите доказательство теоремы.
Доказательство:

1. Построим плоскость AMH .

2. Докажем, что прямая а  AMH .

а) а  НМ (по условию),

б) а  АН, т.к. АН  α , а  α ;

в) НМ ∩ АН = Н
Значит, а  AM (по определению прямой, перпендикулярной плоскости)
A
A
A
а  AMH
(по признаку)
?
M
M
M
H
H
H
α
a
a

Сравните свое оформление с приведенным. Какие выводы для себя можно сделать?

Справедлива, также и обратная теорема .
Составьте краткую запись.
Сформулируйте обратную теорему
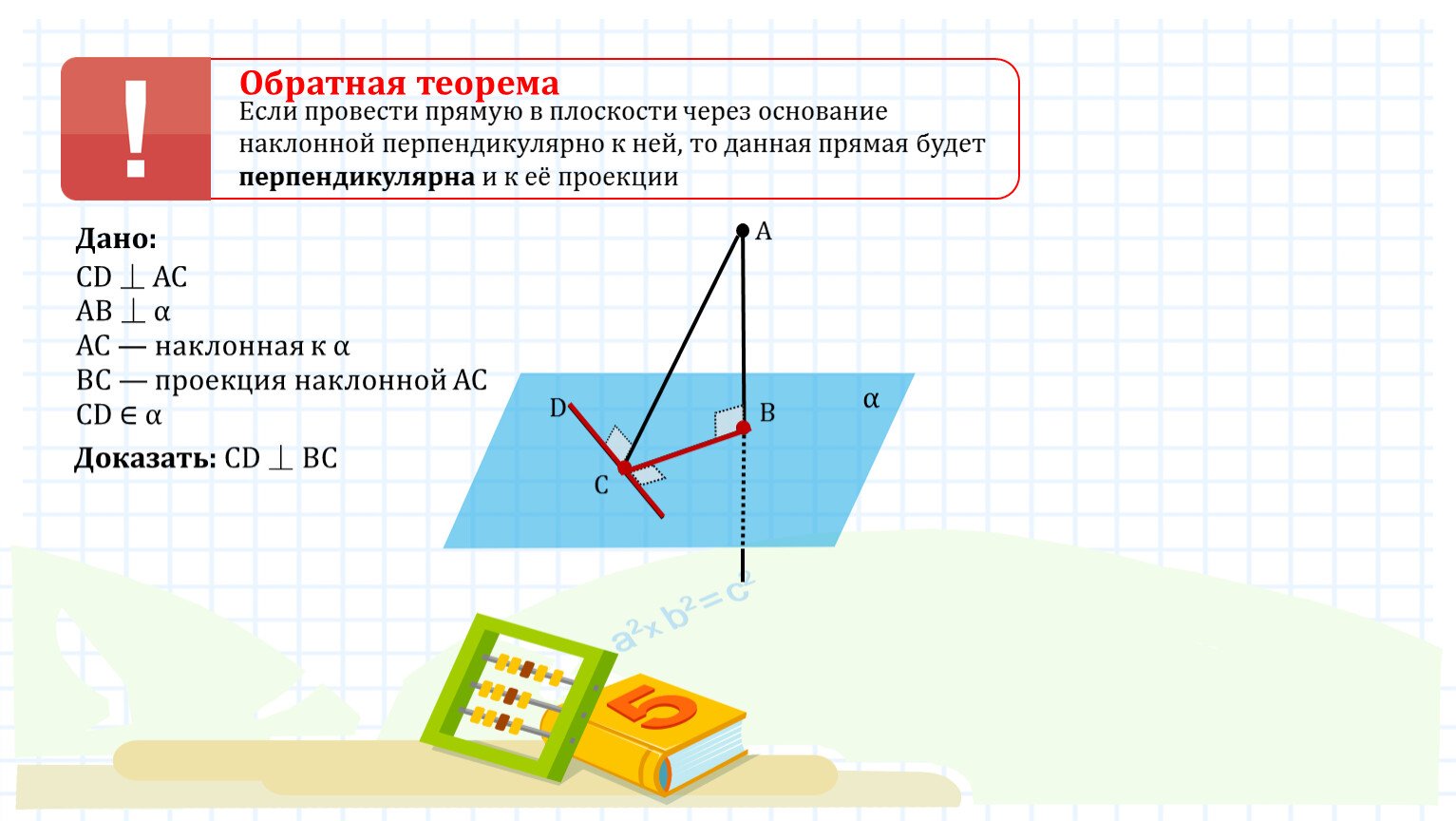
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Дано: плоскость α ,
прямая a , a  α
MA- наклонная, M є a ,
AH  α ,
HM -проекция наклонной,
а  НМ
A
?
M
H
H
a
Доказать:
а  АМ
Доказательство обратной теоремы рассмотрите самостоятельно

Какие фигуры необходимо выделить на чертеже, чтобы доказать перпендикулярность двух прямых, используя теорему о трех перпендикулярах?
Какие фигуры надо
ра c смотреть в задаче?
?
АВС D
Плоскость
Прямая, лежащая в плоскости
В D
?
?
Наклонная
M О
Проекция
?
OC
Перпендикулярность каких фигур известна?
Какой вывод делаем?
Решение:

В D  АВС D ;
В D  ОС (по свойству ромба),

ОС – проекция МО

В D  МО (по теореме о трех перпендикулярах),

Источник: https://multiurok.ru/files/teorema-o-trekh-perpendikuliarakh-2.html

Различные способы доказательства теоремы о трех перпендикулярах и её применение при решении задач

Управление образования и науки исполкома
Криворожского городского совета
Криворожская общеобразовательная школа № 124
Различные способы доказательства теоремы о трех перпендикулярах и её применение при решении задач
Подготовила учитель математики
КОШ № 124
Переходько Татьяна Николаевна
г. Кривой Рог
2018

Тема урока. Различные способы доказательства теоремы о трех перпендикулярах и её применение при решении задач.

Цели урока:

Образовательные – повторить понятие расстояния от точки до плоскости и теорему о трех перпендикулярах; показать применение этой теоремы при решении задач; обеспечить восприятие учебного материала с помощью презентаций;
Развивающие – способствовать формированию ключевых компетенций, а также активизации творческой деятельности учащихся;
Воспитательные – содействовать воспитанию интереса к математике, умение четко организовать работу.

Тип урока: урок первичного закрепления новых знаний.
Технологии: информационные технологии
Оборудование: медиапроектор, экран, мультимедийная программа Microsoft PowerPoint.
План урока.

Организационный момент
Презентация по повторению перпендикулярных прямых и прямых, перпендикулярных плоскости.
Проверка домашнего задания (доказательство теоремы о трех перпендикулярах тремя способами).
Физкультминутка
Решение задач по готовым чертежам.
Итог урока
Домашнее задание.

Ход урока

Сегодня мы продолжаем работу над теоремой о трех перпендикулярах, при доказательстве которой используются различные способы. Мы рассмотрим три из них, но существуют ещё несколько способов доказательства: метод от противного, векторный, и некоторые другие.

2.Презентация

В начале урока мы посмотрим небольшую презентацию по повторению перпендикулярных прямых и прямых, перпендикулярных плоскости. Вопросы по презентации

Угол между прямыми равен 90°. Как называются такие прямые? (перпендикулярные)
Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?» (да.)
Продолжите предложение: «Прямая перпендикулярна плоскости, если она…» (перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости.)
Что можно сказать о двух (3-х, 4-х) прямых, перпендикулярных к одной плоскости? (Они параллельны.)
Две прямые, перпендикулярные третьей прямой, … (параллельны)
Как определяется расстояние от точки до прямой на плоскости? (Возможный ответ: как кратчайшее расстояние от точки до прямой, как длина перпендикуляра, проведенного из точки к данной прямой).

Проверка домашнего задания

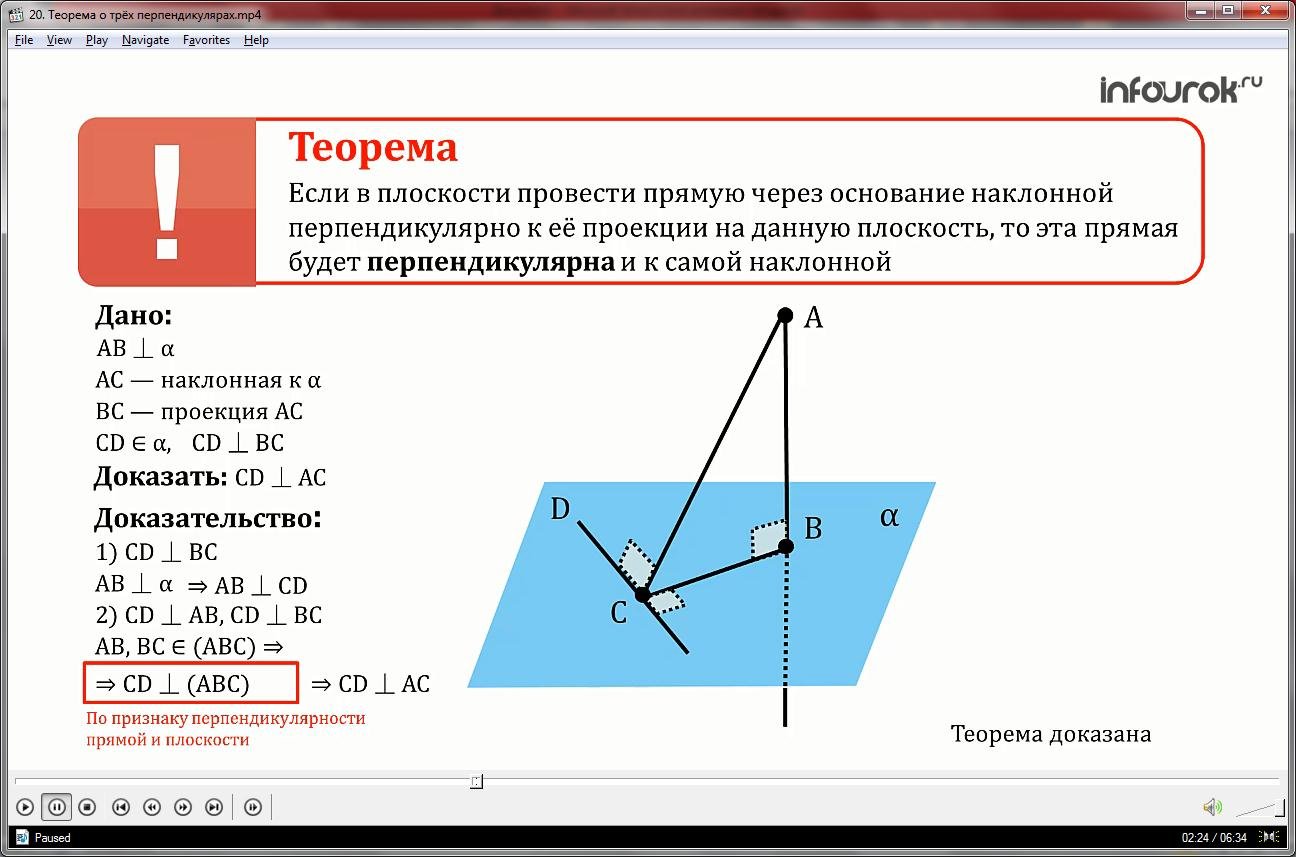
Теорема: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной

Доказательство:

Обратимся к рисунку, на котором отрезок АВ – перпендикуляр к плоскости π, АС – наклонная, m – прямая, проведенная в плоскости π через точку С перпендикулярно к проекции СВ наклонной. Докажем, что m АС. Рассмотрим плоскость АСВ.

Прямая m перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым АВ и ВС, лежащим в плоскости АСВ (m ВС по условию и m AB, так как АВ π). Отсюда следует, что прямая m перпендикулярна к любой прямой, лежащей в плоскости АВС, в частности m АС. Теорема доказана.

2 способ доказательства теоремы о трех перпендикулярах.

От точки А отложим равные отрезки: АМ= АN. Точки М и N соединим с точками O и S. В ОА есть одновременно высота и медиана, этот треугольник равнобедренный: ОМ = ОN. Прямоугольные треугольники OSM и OSN равны (по двум катетам). Из их равенства следует, что SM= SN и SA- медиана равнобедренного треугольника MSN. Значит, SA одновременно и высота этого треугольника, т. е. SA┴MN.

3 способ доказательства теоремы о трех перпендикулярах.

На прямой t возьмем произвольную точку В и соединим ее с точками О и S. Из прямоугольных треугольников SOB, SOA и AOB: = SO2+ OB2, SA2 = =SO2+ OA2, OB2- OA2= AB2. Вычтя из первого равенства второе, получим:SB2 – SA2 = =OB2 – OA2. Приняв во внимание третье равенство, будем иметь: SB2 – SA2= AB2, SB2 = SA2 +AB2. Согласно теореме, обратной теореме Пифагора, SA┴AB, т. е. t┴SA

4.Физкультминутка
Время тратить мы не будем, поднимаем кверху руки,
Опускаем их на плечи, продолжаем дальше вместе.
Поднимаем, опускаем, от урока отдыхаем.
Руки вверх над головой, смотрим все перед собой,
Позвоночник выпрямляем, локти сводим, распрямляем,
Организм оздоровляем, кислородом наполняем.
Чтобы ноги поразмять, будем дружно приседать,
Встали, кверху потянулись, повторили, улыбнулись.
Заряд бодрости поможет нам опять урок продолжить.

5. Решение задач по готовым чертежам.

1 Условие: в треугольнике АВС угол С равен 90°, ВК перпендикулярна плоскости треугольника АВС. Доказать, что КС перпендикулярна АС.

Решение:

ВК перпендикулярен АВС, КС – наклонная, ВС – проекция. ВС перпендикулярен АС так как угол С равен 90°, значит КС перпендикулярен АС по теореме о трех перпендикулярах.

2 Условие: АВСD – квадрат, ВК перпендикулярен плоскости квадрата, О – точка пересечения диагоналей квадрата. Доказать, что КО перпендикулярен АС.

Решение:

ВК перпендикулярен плоскости квадрата, ВО – проекция, КО – наклонная, ВО перпендикулярен АС так как диагонали квадрата взаимно перпендикулярны. Значит, КО перпендикулярен АС по теореме о трех перпендикулярах.

3 Условие: АВСD – квадрат, АВ = 2 см, ВК перпендикулярен плоскости квадрата, ВК = 2. Найти площадь треугольника АКD.

Решение:

КВ перпендикулярен плоскости квадрата, АК – наклонная, АВ – проекция. АВ перпендикулярен АD, так как АВСD – квадрат. Значит, АК перпендикулярен АD по теореме о трех перпендикулярах. Значит, треугольник АКD – прямоугольный. Площадь треугольника АКD равна половине произведения АК на АD. В треугольнике АВК: по теореме Пифагора АК2=КВ2+АВ2==12+4=16. АК =

Значит площадь треугольника АКD равна см2.
Ответ: 4 см2.
Итог урока.

Сегодня мы ещё раз повторили теорему о трех перпендикулярах и рассмотрели некоторые задачи по готовым чертежам. 7. Домашнее задание.

§2 п. 19 и 20, №148.

Источник: https://vseosvita.ua/library/razlicnye-sposoby-dokazatelstva-teoremy-o-treh-perpendikularah-i-ee-primenenie-pri-resenii-zadac-78823.html

Теоретические материалы: Пространственные фигуры и их изображение на плоскости. Скрещивающиеся прямые

Стереометрия

9. Прямые и плоскости в пространстве

9.1. Пространственные фигуры и их изображение на плоскости. Скрещивающиеся прямые. Основные свойства плоскости

Определение

Фигура, не все точки которой лежат в одной плоскости, называется пространственной.

К пространственным фигурам, кроме геометрических тел, относятся двугранные и многогранные углы и другие совокупност точек, линий, поверхностей. Основные элементы, из которых состоят пространственные фигуры, это точки, прямые, плоскости. Любую фигуру можно свободно перемещать в пространстве, не изменяя ее размеров и формы.

Определение

Две фигуры называются равными, если их можно совместить всеми их точками.

Стереометрия изучает свойства пространственных фигур. Две прямые в пространстве могут лежать в одной плоскости, и тогда они будут либо пересекающимися, либо параллельными.

Определение
Две прямые называются скрещивающимися, если одна из них не лежит ни в одной из бесконечного множества плоскостей, проходящих через другую прямую.
Изображение (чертёж или рисунок) пространственной фигуры на плоскости выполняется по правилам параллельного проектирования, которые нужно знать и при чтении чертежа.
а) Если прямые в пространстве параллельны, то и их проекции на чертеже параллельны или совпадают; если прямые на чертеже параллельны, то соответствующие им прямые в пространственной фигуре являются параллельными.

б) Если прямые на чертеже пересекаются, то соответствующие им прямые в пространстве пересекаются либо скрещиваются. Путем перехода от плоского чертежа пространственной фигуры к ее модели (материальной или воображаемой) необходимо научиться уверенно различать пересекающиеся и скрещивающиеся прямые. Без этого невозможно изучать стереометрию.

в) Отношение отрезков параллельных прямых (или одной прямой) в пространственной фигуре равно отношению соответствующих им отрезков на чертеже. Отсюда следует, что в одной группе параллельных отрезков при переходе от пространственной фигуры к чертежу каждый отрезок сокращается в одно число раз, а в другой группе параллельных отрезков — в другое (но постоянное для этой группы) число раз.

г) Углы пространственной фигуры на ее чертеже обычно изменяют свою величину, например прямой угол пространственной фигуры может быть изображен острым или тупым углом.
Невидимые линии пространственной фигуры на чертеже изображаются штриховыми линиями.
Основные свойства плоскости выражаются следующими математическими предложениями.
Аксиома 1
Если две точки прямой лежат на плоскости, то и все точки этой прямой лежат на плоскости.
Аксиома 2
Через три точки, не лежащие на одной прямой, можно провести плоскость, притом только одну.
Аксиома 3
Если две плоскости имеют общую точку, то они имеют общую прямую, проходящую через эту точку, то есть пересекаются.
Следствие 1
Через прямую и точку, не лежащую на этой прямой, можно провести плоскость, притом только одну.
Следствие 2
Через две пересекающиеся прямые можно провести плоскость и только одну.
Следствие 3
Через две параллельные прямые можно провести плоскость, притом только одну.

Источник: https://dl.bsu.by/mod/book/view.php?id=10186&chapterid=1334

Тема: Теорема о трех перпендикулярах. Цели: изучение теоремы (доказательство теоремы разными способами); формирование навыков решения задач с использованием. — презентация

2 Тема: Теорема о трех перпендикулярах. Цели: изучение теоремы (доказательство теоремы разными способами); формирование навыков решения задач с использованием теоремы; развитие логической культуры учащихся. Тип урока : получение новых знаний. Оборудование: мультимедийная доска, ПК, карточки с заданиями, учебник.

3 На этом уроке учащиеся ознакомятся с важными теоретическими знаниями, которые они смогут применять для нахождения расстояния от точки до прямой в пространстве. I.Организационный момент. II.Формирование цели и задачи урока, мотивация учебной деятельности. a α А Как найти расстояние от точки А до прямой а?

4 В каких задачах используют теорему о трех перпендикулярах? На рисунках 1-4 МА перпендикулярна плоскости АВС. По рисункам обоснуйте расстояние от точки М до прямой ВС. A B D C M M A B C D ADC=90

5 В каких задачах используют теорему о трех перпендикулярах? На рисунках 1-4 МА перпендикулярна плоскости АВС. По рисункам обоснуйте расстояние от точки М до прямой ВС. D C A M ABCD — ромб A C B M ВС – касательная к окружности

6 III.Актуализация опорных знаний. Что называют перпендикуляром к плоскости? Что называют наклонной к плоскости? Что называют основанием перпендикуляра? Что называют основанием наклонной? А BC α A BC a

7 IV.Восприятие нового материала. Теорема: если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной. Доказательство теоремы проводится с использованием программы «УМК живая математика»

9 Первый шаг От точки А отложим MA=AN. Соединим M и N с S и O. В этом случае AO одновременно медиана и высота. Следовательно MON – равнобедренный треугольник, где NO=OM.

10 Второй шаг Прямоугольные треугольники SOM и SON равны по двум катетам ( NO=OM, SO – общая сторона).

11 Третий шаг Из предыдущего шага следует, что NSM – равнобедренный треуогольник, а значит SA – одновременно медиана и высота. То есть AS перпендикулярна MN, что и требовалось доказать.

12 Доказательство 2 Допустим, что SA не перпендикулярна прямой l. Проведем SB l, тогда SA>SB. Из прямоугольных треугольников SOA и SOB: OA 2 =SA 2 -SO 2. OB 2 =SB 2 -SO 2 Получаем: OA>OB. Между тем OA

13 Доказательство 3 На прямой m отметим произвольную точку B и соединим с точками O и S. Из прямоугольных треугольников SOB, SOA, OAB: SB²=SO²+OB²; SA²=SO²+OA²; OB²=OA²=AB²; S O B C A m

14 Доказательство 3 Вычтя почленно из первого равенства второе, получим: SB²=SA²=OB²=OA² Приняв во внимание третье равенство, будем иметь: SB²=SA²=AB². SB²=SA²+AB². Согласно обратной теореме Пифагора: SA AB, т.е. m SA.

15 V.Решение задач: Учебник 5.39, Дано: DA (ABC), угол BAC=30°, угол ABC=60° Доказать: СВ AC. А B C D Дано: DA (ABC), угол BAC=40°, угол ACB=50° Доказать: СВ BD. АB D C

16 Математический диктант ABCD – прямоугольник, SA (ABC). Вариант 1 – SA= см, AB = 1 см, AD = 3 см; Вариант 2 – SA= см, AB = 1 см, AD = 2 см; Пользуясь изображением, найдите: 1)Длину отрезка SB; (2 балла) 2)Длину диагонали AC; (2 балла) 3)Длину отрезка SD; (2 балла) 4)Величину угла SBC; (2 балла) 5) Величину угла SDC; (2 балла) 6)Площадь треугольника SDC. (2 балла) B С D A S

17 Ответы Вариант 1 1)2 см; 2) см; 3) см; 4)90°; 5)90°; 6) см Вариант 2 1) см; 2) см; 3) см; 4)90°; 5)90°; 6) см;

18 VI.Домашнее задание: 1)§ 5.3, теорема. 2)N 5.63 – учебник. 3)«Разноуровневые дидактические материалы» под редакцией А.П. Ершовой. С-10 по вариантам уровни: АN 1; 2. Б N 3

19 VII. Подведение итогов урока Вопросы к классу: 1)Сформулировать теорему о тех перпендикулярах. 2)Какие теоремы и определения использовали для доказательства этой теоремы? 3)Укажите взаимное расположение прямых a и b. ABCD – квадрат, SB (ABC) ABCD – ромб, SB (ABC) C DA B S a b O A B C D b a S

20 Спасибо за внимание!

Источник: http://www.myshared.ru/slide/673612/